Для ввода информации о математических моделях элементов структурной схемы системы управления в меню File выполнить команду Import… (импортировать). Открывается окно Import System Data, позволяющее различными способами вводить информацию в проектируемую систему. В настоящей работе математические модели системы задаются соответствующими передаточными функциями. Пусть, например, в некоторый блок требуется ввести математическую модель, представленную передаточной функцией 
. Тогда в текстовое поле данного блока необходимо ввести конструкцию вида 
Установить передаточную функцию объекта управления (ОУ) 
в виде:
, (3.1)
с параметрами 
; Т1=2 с; Т2=1,5 с; 
.
2.1. Ввести передаточную функцию регулятора 
, а передаточные функции предварительного фильтра и датчика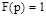 
и 
. Заметим, что коэффициент усиления регулятора можно установить непосредственно в текстовом поле 
текущего регулятора Current Compensator окна SISO Design Tool. В этом случае после установки нового значения коэффициента усиления необходимо щелкнуть в поле графиков логарифмических характеристик для отображения их нового вида.
Определить устойчивость замкнутой системы:
а) по логарифмическим частотным характеристикам разомкнутой системы;
б) по критерию Найквиста;
в) по корням характеристического уравнения.
Кроме логарифмических частотных характеристик необходимо отобразить переходную характеристику замкнутой системы и диаграмму Найквиста. С этой целью в меню Tools (инструменты) окна SISO Design Tool выбрать подменю Loop Responses и установить галочки напротив команд Closed – Loop Step и Open – Loop Nyquist. В результате открывается окно просмотрщика LTI Viewer for SISO Design Tool, в котором отображается переходная характеристика замкнутой системы (Step Response) и диаграмма Найквиста (Nyquist Diagram).
Для получения корней характеристического уравнения замкнутой системы в меню View окна SISO Design Tool выполнить команду Closed – Loop Poles.
Выписать значения корней характеристического уравнения из колонки таблицы Pole Value окна Closed – Loop Pole Viewer, после чего закрыть данное окно.
Логарифмические частотные характеристики разомкнутой системы отображаются в основном окне SISO Design Tool. В левых нижних углах графических окон с изображением логарифмических частотных характеристик содержится информация об устойчивости замкнутой системы (Stable loop – замкнутая система устойчива), а также о запасах устойчивости (G.M.: - запас устойчивости по амплитуде, Р.М.: - запас устойчивости по фазе).
Логарифмические частотные характеристики, переходная характеристика замкнутой системы и диаграмма Найквиста должны быть сохранены на диске для последующей подготовки отчета по лабораторной работе.
2.2. Увеличить коэффициент усиления регулятора в два – три раза, установив его в поле Gurrent Compensator 
. Для отображения новых характеристик системы щелкнуть в поле графиков окна SISO Design Tool. Определить устойчивость замкнутой системы аналогично п.2.1. Сохранить полученные результаты на диске.
2.3. Определить граничное значение коэффициента усиления. С этой целью навести указатель мыши на график логарифмической амплитудно-частотной характеристики. При этом указатель принимает форму кисти руки. Удерживая нажатой левую клавишу мыши перемещать логарифмическую амплитудно-частотную характеристику вверх-вниз, что равносильно соответственно увеличению или уменьшению коэффициента усиления разомкнутой системы, добиться приближенного равенства нулю запасов устойчивости по амплитуде и по фазе. Отпустить левую клавишу и определить значение критического коэффициента усиления в текстовом поле Current Compensator C(s) =.
3. Исследовать влияние интегрального (И), пропорционально – интегрального (ПИ) и пропорционально – интегрально – дифференциального (ПИД) регуляторов на устойчивость системы с объектом, передаточная функция которого имеет вид:
. 
(3.2)
Численные значения параметров ОУ приведены в таблице.
| Параметры объекта | Варианты | |||||
| 1,2 | 1,5 | 1,8 | |||
| 1,1 | 1,2 | 0,4 | 0,5 | 0,8 |
3.1. Установить передаточную функцию объекта управления (3.2) в окне Import System Data в текстовом поле G =. Ввести в систему И – регулятор с передаточной функцией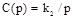 
, 
. Передаточная функция регулятора вводится в текстовом поле 
. Определить устойчивость замкнутой системы по корням характеристического уравнения и полученным характеристикам системы. Результаты сохранить на диске.
3.2. Изменить коэффициент усиления регулятора 
, и проделать п.3.1.
3.3. Не меняя объект управления (3.2) ввести в систему ПИ – регулятор с передаточной функцией
, 
; 
.
Определить устойчивость замкнутой системы. Результаты моделирования сохранить на диске.
3.4. Изменить в регуляторе коэффициент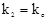 
и проделать п.3.3.
3.5. Не меняя объект управления ввести в систему ПИД – регулятор с передаточной функцией
,
; 
; 
; 
.
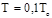Определить устойчивость замкнутой системы. Результаты сохранить на диске.
Содержание отчета
1. Распечатка результатов моделирования (одна на бригаду).
2. По критерию Гурвица определить устойчивость замкнутой системы, исследуемой в п.2.
3. Для заданного преподавателем типа регулятора построить асимптотические ЛАЧХ и ЛФЧХ разомкнутой системы и сделать вывод об устойчивости замкнутой системы.
Контрольные вопросы
1. Как получают уравнение 
приведенной системы?
2. Каким образом исходное уравнение приведенной системы линеаризуется?
3. В каких случаях по корням характеристического уравнения линеаризованной системы можно определить устойчивость тривиального решения приведенной системы, и в каких нельзя?
4. По критерию Гурвица сформулируйте условия, при которых характеристическое уравнение имеет: а) левые корни; б) правые;
в) корни на мнимой оси.
5. Сформулируйте условия устойчивости, неустойчивости, границы устойчивости используя АФХ разомкнутой системы.
6. Используя аналогию между АФХ разомкнутой системы и ее ЛЧХ, сформулируйте условия устойчивости, неустойчивости, используя ЛЧХ разомкнутой системы.
7. Поясните термин критический коэффициент усиления и укажите методику его определения по критериям Гурвица и Найквиста.
8. Определите термин запасы устойчивости по амплитуде и фазе. Укажите методики их определения по критерию Найквиста.
9. Передаточная функция разомкнутой системы имеет вид:
.
Определить устойчивость замкнутой системы по критерию Найквиста.
10. Передаточная функция разомкнутой системы имеет вид:
.
Определить устойчивость замкнутой системы по критерию Гурвица.
Лабораторная работа № 3 
