Для наглядного представления частотных свойств звеньев используются частотные характеристики, которые описывают вынужденное движение звена при входном гармоническом воздействии и имеют простую физическую интерпретацию. Пусть на вход динамического звена с передаточной функцией W(s) воздействует гармонический сигнал v(t) = A0sinωt с амплитудой A0 и угловой частотой ω.
На выходе устойчивого звена после завершения переходного процесса (т.е. в установившемся режиме) будет наблюдаться также гармонический сигнал yуст(t) = A1(ω)sin[ωt + φ(ω)] той же частоты, амплитуда A1(ω) и фаза φ(ω) которого зависят от частоты входного воздействия.
Отношение амплитуд сигналов на выходе и входе звена R(ω) = A1(ω) / A0, определяющее коэффициент передачи звена на различных частотах, называется амплитудно-частотной характеристикой (АЧХ). Другими словами АЧХ показывает, как изменяется амплитуда выходного сигнала звена при изменении частоты.
Функция φ(ω) называется фазовой частотной характеристикой (ФЧХ) звена. Она показывает как изменяется фаза выходного гармонического сигнала на различных частотах.
Основной частотной характеристикой звена является амплитудно-фазовая характеристика (АФХ), представляющая собой комплексную функцию W(jω), модуль которой равен АЧХ, а аргумент – ФЧХ, т.е.
|W(jω)| = R(ω), arg W(jω) = φ(ω).
АЧХ является четной функцией частоты, а ФЧХ – нечетной.
В общем случае АФХ определяют как отношение изображений Фурье выходной и входной величин звена при нулевых начальных условиях
W (jω) = Y(jω) / V(jω) = W(s)| s = j ω
и получают на практике из передаточной функции подстановкой s=jω. Функцию W(jω) еще называют частотной передаточной функцией, поскольку она определяет установившуюся реакцию звена на гармонический входной сигнал.
Математически АФХ можно записать в показательной или алгебраической формах:
W (j ω) = R (ω) е j φ (ω) = U (ω) + j V (ω),
где U(ω) = Re{W(jω)} и V(ω) = Jm{W(jω)} – вещественная и мнимая частотные характеристики. Указанные выше частотные характеристики связаны между собой следующими соотношениями:
АФХ изображается на комплексной плоскости (U, jV) в виде годографа, т.е. совокупности точек, соответствующих значениям функции W(jω) = U(ω) + jV(ω) при изменении частоты от нуля до бесконечности. Для отрицательных значений частот АФХ находится как зеркальное относительно вещественной оси отображение характеристики для положительных частот. Функцию W(jω), построенную при изменении 
называют диаграммой Найквиста. Таким образом, АФХ или совокупность АЧХ и ФЧХ полностью определяют частотные свойства динамического звена.
На практике широкое распространение получили логарифмические частотные характеристики (ЛЧХ): логарифмическаяамплитудно-частотная характеристика (ЛАЧХ) и логарифмическая фазовая частотная характеристика (ЛФЧХ). ЛАЧХ представляет собой график зависимости 20lg |W(jω)| от lgω, ЛФЧХ – график зависимости φ(ω) от lgω.
В том случае, когда звено является минимально-фазовым, его свойства однозначно оцениваются амплитудно-частотной характеристикой. Минимально-фазовым называют динамическое звено, все нули и полюсы передаточной функции которого имеют отрицательные или нулевые вещественные части [5].
Построение ЛАЧХ звена экспериментальным путем осуществляют следующим образом. На вход исследуемого звена подают гармонический сигнал с постоянной амплитудой А0, частота которого изменяется в определенном диапазоне, и производят измерение амплитуды A1(ω) выходного сигнала звена в установившемся режиме. По оси абсцисс графика ЛАЧХ откладывается угловая частота ω в логарифмическом масштабе (т.е. lgω), а по оси ординат- значение L(ω) = 20lg|W(jω)| = 20lg|A1(ω)/A0| на данной частоте, выраженное в децибелах (дб).
В некоторых случаях целесообразно строить асимптотическую ЛАЧХ. Пусть передаточная функция записана в стандартной форме 
причем передаточная функция 
содержит только сомножители вида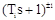 
или 
. Тогда правило построения асимптотической ЛАЧХ заключается в следующем [5]:
-определяются сопрягающие частоты 
, соответствующие всем сомножителям передаточной функции W(s), и откладываются на логарифмической оси частот;
- строится низкочастотный участок ЛАЧХ, представляющий собой прямую, имеющую наклон –20*υ дб/дек, и проходящую при частоте ω= 1 через точку с ординатой 20 lg k(дб);
- после каждой из сопрягающих частот, начиная с наименьшей, изменяется наклон характеристики на ±20 дб/дек или на ±40 дб/дек в зависимости от того, какому сомножителю соответствует эта сопрягающая частота 
или 
.Знак (+) или (-) ставится в зависимости от того, в числителе или знаменателе передаточной функции расположен этот сомножитель;
Наибольшее отличие асимптотической ЛАЧХ от точной характеристики L(ω) наблюдается в области значений ω, расположенных вблизи сопрягающих частот ωi.
3.Порядок выполнения лабораторной работы
1. Запустить систему MATLAB 6X.
После завершения инициализации в командном окне выполнить команду simulink. В результате открывается окно Simulink Library Browser (библиотека блоков SIMULINK). Для проведения моделирования необходимо открыть окно для создания S – модели, щелкнув на кнопке в виде чистого листа 
на панели инструментов окна Simulink Library Browser.
Разработка моделей средствами SIMULINK основана на технологии drag-and-drop (”перетащи и оставь”). Нужные блоки из библиотеки перетаскиваются с помощью мыши в окно модели. Затем соответствующие входы блоков соединяются протягиванием мыши с нужными выходами блоков исходя из логики работы модели.
2. Экспериментально снять амплитудно-фазовую характеристику апериодического звена 1 порядка. Параметры звена указаны в табл. 2 (номер варианта соответствует номеру бригады).
Для осуществления моделирования построить структуру модели, представленную на рис. 1
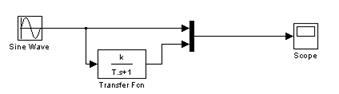
Рис. 1.
Все блоки модели находятся в основном разделе библиотеки Simulink: блок Sine Wave (генератор гармонического сигнала) в разделе Sources (источники); блок Transfer Fcn (передаточная функция) в разделе Continuous (блоки для моделирования непрерывных систем); блок Mux (мультиплексор) в разделе Signals & Systems (сигналы и системы); блок Scope (осциллограф) в разделе Sinks (получатели). Чтобы открыть окно настройки параметров блока, нужно поместить его в окно блок – диаграммы и дважды щелкнуть на нем.
Для блока Sine Wave установить следующие параметры: Sine type в режиме Time-based; значение амплитуды и частоты гармонического сигнала равные единице. Остальные параметры установить равными нулю. Щелкнув на кнопке “OK” закрыть окно настроек блока.
В блоке Transfer Fcn установить численные значения параметров передаточной функции в соответствии с номером варианта. Для этого необходимо ввести коэффициенты полинома числителя передаточной функции в поле Numerator и коэффициенты полинома знаменателя в поле Denominator. Указанные коэффициенты вводятся в квадратных скобках слева направо по убывающим степеням s, разделенные пробелом. Блоки Mux и Scope не требуют первоначальной настройки.
После установки параметров всех блоков модели необходимо задать параметры моделирования. С этой целью в меню Simulation окна блок – диаграммы выполнить команду Simulation parameters… (параметры моделирования). В открывшемся диалоговом окне на вкладке Solver (решатель) установить следующие параметры моделирования: Start time=0 (начало моделирования); Stop time = 10 (окончание моделирования).
Группа параметров Solver options (параметры решателя) определяет метод реализации (расчета) модели с помощью двух раскрывающихся списков Type (тип). Установить в первом списке (слева) способ изменения модельного времени Fixed–step (фиксированный шаг), а во втором списке выбрать метод расчета нового состояния системы ode 5 (Dormand – Prince). В поле Fixed step size (величина фиксированного шага) установить значение 0.005. Щелкнув на кнопке “OK” закрыть окно настроек параметров моделирования. Для запуска модели необходимо щелкнуть в панели инструментов окна блок-диаграммы на кнопке в виде черного треугольника. Дважды щелкнув на блоке Scope можно наблюдать результаты моделирования.
Развернуть окно Scope во весь экран. Измерить амплитуду выходного сигнала звена и фазовый сдвиг между выходной и входной гармониками после окончания переходного процесса. Для точного измерения фазового сдвига необходимо выделить с помощью мыши область графика, в которой кривые пересекают ось абсцисс, и измерить интервал времени 
t между точками пересечения. Величина фазового сдвига определяется как 
t. Моделирование провести для значений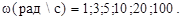 
Для значений 
10 целесообразно изменить время окончания моделирования с 10 до 1. Если щелкнуть в панели инструментов окна Scope на кнопке в виде бинокля – это приведет к установке оптимального масштаба координатных осей для отображаемых графиков.
Результаты моделирования свести в табл.1:
Таблица 1
 (рад/с)
|
|
|
|
Значение фазового сдвига в градусах можно вычислить в командном окне MATLAB.
Закрыть окно Scope.
3. Для исследуемого звена получить переходную характеристику, логарифмические частотные характеристики (ЛХЧ) и диаграмму Найквиста.
3.1. Привести блок-схему модели к виду, представленному на рис.2, удалив блок Mux и соответствующие линии связи. Для удаления блока его необходимо выделить, щелкнув на нем мышью, и после этого щелкнуть на кнопке панели инструментов в виде ножниц. Аналогично удаляются и линии связи.
Рис. 2
В блоке Transfer Fcn k и T – численные значения параметров звена.
3.2. В меню Tools (инструменты) исполнить команду Linear analysis…(линейный анализ). В результате открываются два окна – окно основного просмотрщика LTI Viewer и окно указателей входов и выходов анализируемой модели Model_Inputs_and_Outputs. С помощью мыши перетащить указатель Input Point на вход исследуемого звена, а указатель Output Point на выход.
3.3. В меню Simulink просмотрщика LTI Viewer выполнить команду Get Linearized Model (создать линеаризованную модель). При этом в окне просмотрщика LTI Viewer происходит отображение одной из характеристик линейных систем, например переходной характеристики (Step). Для просмотра других характеристик необходимо щелкнуть правой клавишей мыши в поле графика, и в открывшемся контекстном меню на вкладке Plot Type (тип графика) щелкнуть на имени интересующей характеристики. (Bode – логарифмические частотные характеристики, Nyquist –диаграмма Найквиста).
При необходимости изменить масштабы по осям графиков, в меню Edit (правка) исполнить команду Viewer Preferences (свойства средства просмотра). Новые значения масштабов устанавливаются на вкладке Parameters (параметры) диалогового окна LTI Viewer Preferences после сброса флажков автоматической генерации масштабов.
Сохранить полученные характеристики для последующей подготовки отчета по лабораторной работе целесообразно следующим образом.
3.4. В меню Edit (правка) просмотрщика LTI Viewer исполнить команду Plot Configurations (конфигурация графиков), и в открывшемся диалоговом окне выбрать желаемое расположение графиков в окне просмотрщика LTI Viewer. Логарифмические частотные характеристики (Bode), включающие 2 графика, желательно целиком разместить в окне, а переходную характеристику (Step) и диаграмму Найквиста (Nyquist) объединить в виде конфигурации 2, установив соответствующий флажок и название характеристик в полях 1 и 2. После получения графиков в окне просмотрщика LTI Viewer необходимо проделать следующее. В меню File (файл) выполнить команду Print to Figure (печать фигуры) и в открывшемся графическом окне Figure No._ в меню Edit активизировать команду Copy Figure. С помощью этой команды графическое поле окна Figure No._помещается в буфер обмена. Для сохранения результатов работы открыть текстовый редактор Microsoft Word и вставить в открытое окно содержимое буфера обмена. После этого необходимо закрыть графическое окно Figure No._, которое в дальнейшем не используется.
4. Повторить пункт 3 для звеньев 2 – 5 представленных в табл.2 Для этого следует ввести передаточную функцию нового звена в блок Transfer Fcn исследуемой модели.
Затем открыть окно просмотрщика LTI Viewer, активизировать меню Edit (правка) и в подменю Systems (системы) выполнить команду Refresh (обновить). В открывшемся диалоговом окне Updating the LTI Viewer (обновить характеристики систем) в ответ на вопрос Do you want to remove these systems from LTI Viewer? (Вы хотите удалить характеристики этих систем из окна просмотра?) щелкнуть на кнопке Yes (да). Затем в меню Simulink выбрать команду Get Linearized Model (создать линеаризованную модель) и получить требуемые характеристики исследуемого звена. После получения характеристик всех звеньев закрыть окно просмотрщика LTI Viewer.
5. Для апериодического звена с запаздыванием получить переходную характеристику и построить амлитудно – фазовую характеристику (АФХ).
Схема модели для построения переходной характеристики представлена на рис. 3.
Рис. 3
Предварительно из окна блок – схемы модели удалить блок Sine Wave и указатели Input Point и Output Point. Блок Step (скачок) находится в основной библиотеке Simulink в разделе Sources (источники), а блок Transport Delay (звено запаздывания) в разделе Continuous (блоки для моделирования непрерывных систем). Установить значение параметра Final Value (конечное значение) блока Step равным единице. Остальные параметры этого блока установить равными нулю. Задать численные значения параметров k и T в блоке Transfer Fcn (передаточная функция). В блоке Transport Delay установить численное значение параметра 
в поле Time delay (время запаздывания). После установки параметров всех блоков установить следующие параметры моделирования: Start time = 0; Stop time = 10; способ изменения модельного времени – Variable-step (переменный шаг); метод расчета нового состояния системы – любой из раскрывающегося списка.
Запустить модель на исполнение щелкнув на соответствующей кнопке панели инструментов окна блок диаграммы. Открыть окно блока Scope и наблюдать переходную характеристику.
Выражение для амплитудно-фазовой характеристики исследуемого звена можно получить, заменив в передаточной функции s=jw. В результате имеем:
, 
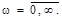
Для построения рассматриваемой характеристики исполнить в командном окне следующий фрагмент программы, подставив численные значения параметров k и T.
AFX = k* exp (- 
Plot (AFX);
Grid on;
Переходную характеристику и АФХ исследуемого звена сохранить на диске.
Содержание отчета
1. Распечатка результатов моделирования, полученных в п. 3, 4, 5 (одна на бригаду).
2. По результатам выполнения п.2 построить АФХ апериодического звена 1 порядка.
3. Для заданного преподавателем звена:
а) по передаточной функции определить выражение для переходной характеристики h(t);
б) по полученной в результате моделирования переходной характеристике звена определить его параметры;
в) привести выражения для W(jw), R(w) и j(w);
г) построить асимптотическую ЛАЧХ.
Контрольные вопросы
1. Пояснить физический смысл амплитудно-фазовой характеристики.
2. Передаточная функция звена имеет вид:
.
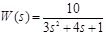