Критериями устойчивости называют правила, позволяющие оценивать местоположение корней характеристического уравнения линейных систем на комплексной плоскости без их непосредственного вычисления. Для оценки местоположения корней критерии оперируют с характеристиками систем, тесно связанными с характеристическим уравнением.
По критериям особенно удобно определять устойчивость систем, заданных структурными схемами в виде, показанном на рис. 2.1, где передаточная функция разомкнутой системы
(2.4)
 |
V(s) E(s) Y(s)
-
Рис. 2.1
является отношением многочленов:
В(s) = b0 sm + b1sm-1 + …+ bm;
D(s)=d0sn+d1sn-1+ …+ dn, n ≥ m. (2.5)
Уравнение D(s)=0 является характеристическим уравнением разомкнутой системы.
Все критерии устойчивости делят, в основном, на две группы: алгебраические и частотные.
Алгебраические критерии для оценки устойчивости оперируют с коэффициентами 
характеристического уравнения замкнутой системы
Д(s)=D(s)+B(s)=a0sn+a1sn-1+…+an. (2.6)
Наиболее известными среди них являются критерии Рауса, Гурвица, Льенара-Шипара [2]. Частотные критерии для оценки устойчивости используют различные частотные характеристики, такие как Д(jω) = Д(s)| s = jω; W(jω) = W(s)|s = jω; L(ω) = 20lg |W(jω)| и φ(ω) = arg W(jω). Наиболее известными являются критерии Михайлова, Найквиста, логарифмический критерий устойчивости [5].
Критерий Гурвица
Критерий Гурвица использует для оценки местоположения корней уравнения Д(s)=0 коэффициенты . Прежде всего проверяется необходимый признак устойчивости вида ai > 0, i = 
. Если он не выполняется, то система не является асимптотически устойчивой. При этом дальнейший анализ устойчивости, как правило, нецелесообразен. При выполнении условия ai>0, i= 
составляется матрица Гурвица по следующему правилу. По главной диагонали последовательно выписывают все коэффициенты 
характеристического многочлена (2.6), начиная с а1. Вниз от элементов главной диагонали столбцы заполняют коэффициентами 
с
последовательно убывающими индексами, и нулями, когда индексы становятся отрицательными. Вверх от главной диагонали столбцы заполняются коэффициентами ai с возрастающими индексами и нулями, когда индекс должен бы быть больше n. Строки матрицы состоят из коэффициентов ai либо только с нечетными, либо только с четными индексами и нулями.
Если диагональные миноры (2.7) матрицы Гурвица положительны (Δi>0, i= 
), то все корни характеристического уравнения Д(s) левые (Re si < 0, i = 
). Если хотя бы один минор Δk, k Î 
матрицы Гурвица отрицателен то, по крайней мере, один из
(2.7)
корней 
правый (
).
Если взять характеристический многочлен устойчивой системы и изменять его коэффициенты так, чтобы система стала неустойчивой, то, по крайней мере, один из миноров Δi матрицы Гурвица должен обратиться в ноль, а затем принимать отрицательные значения. Первым среди Δi обращается в ноль минор Δn-1. В этом случае все корни характеристического уравнения левые, за исключением одной пары чисто мнимых корней. Этот случай называют критическим. Последнее свойство миноров Δi, iÎ 
, называемых еще определителями Гурвица, используют для нахождения критического (граничного) коэффициента усиления разомкнутой системы 
, при котором в характеристическом уравнении есть пара чисто мнимых корней, а остальные левые. Условия для определения k = kкр имеют вид
Δi (k) > 0, i = 
; Δn-1 (k) = 0. (2.8)
Для n = 3 все Δi >0, i =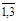 
, если a1 > 0, a1a2 – a0a3 >0. Для n = 4 требуется еще выполнение условия a1a2a3 – a0 a23 – a21a4 > 0.
