ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Методические указания к лабораторным работам
Рязань 2006
УДК 681.51
Теория автоматического управления: Методические указания к лабораторным работам / Рязан. гос. радиотехн. ун-т.; Сост.: Л.П.Карташева, А.М.Никитин, А.И.Уваев / Под ред. проф. А.И.Бобикова. Рязань, 2006. 48 с.
Предназначены для студентов дневной формы обучения специальностей 210100 “Управление и информатика в технических системах”, 071900 “Информационные системы и технологии”, 190900 “Информационно-измерительная техника и технологии”
Ил. 18. Табл. 4. Библиогр.: 9 назв.
Система автоматического управления, передаточная функция, переходная характеристика, устойчивость, критерии устойчивости, возмущающее воздействие, установившаяся ошибка, селективная инвариантность, нули и полюсы, корневой годограф
Печатается по решению методического совета Рязанского государственного радиотехнического университета.
Рецензент: кафедра автоматики и информационных технологий в управлении Рязанского государственного радиотехнического университета (зав. кафедрой проф.Б.А.Алпатов)
Теория автоматического управления
Составители: Карташева Людмила Павловна
Никитин Андрей Михайлович
Уваев Александр Иванович
Редактор
Корректор
Подписано в печать Формат бумаги 60x84 1/16.
Бумага газетная. Печать трафаретная. Усл. печ. л.
Уч.-изд. л.. Тираж экз. Заказ
Рязанская государственная радиотехническая академиия.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТА.
Лабораторная работа № 1
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ДИНАМИЧЕСКИХ ЗВЕНЬЕВ ЛИНЕЙНЫХ САУ
Цель работы
Экспериментальное исследование временных и частотных характеристик динамических звеньев линейных САУ и определение их параметров.
Краткие теоретические сведения
Уравнения и передаточные функции звеньев
Динамическим звеном называют устройство любой физической природы и конструктивного исполнения, описываемое определенным дифференциальным уравнением или передаточной функцией. Иначе, динамическое звено – это математическая модель элемента или соединения элементов САУ [1].
Дифференциальное уравнение, характеризующее поведение (динамику) звена во времени при произвольном входном воздействии, называют уравнением динамики. Установившийся режим звена описывают алгебраическим уравнением, называемым уравнением статики. Этот режим удобно представлять графически с помощью статической характеристики, показывающей зависимость выходной величины звена y от входной v. Статическую характеристику звена можно построить экспериментально, подавая на вход постоянное воздействие 
и измеряя выход 
после окончания переходного процесса, или расчетным путем, используя уравнение статики.
По виду статической характеристики линейные звенья делятся на три группы: позиционные, интегрирующие и дифференцирующие звенья. В звеньях позиционного типа статическая характеристика представляет собой линейную зависимость 
между выходной и входной величинами в установившемся режиме. Коэффициент пропорциональности k называется коэффициентом усиления звена. Если вход и выход звена имеют одинаковую размерность, то коэффициент усиления является безразмерной величиной.
В звеньях интегрирующего типа линейной зависимостью 
связаны производная выходной величины 
и входная переменная 
в установившемся режиме. В этом случае при нулевых начальных условиях будет справедливым равенство 
. Коэффициент пропорциональности k представляет собой коэффициент усиления звена. При одинаковой размерности входной и выходной величин коэффициенту усиления соответствует размерность [c-1].
Звенья дифференцирующего типа характеризуются линейной зависимостью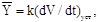 
связывающей выход звена и производную входной величины в установившемся режиме. Коэффициент пропорциональности k также является коэффициентом усиления звена. При одинаковой размерности входа и выхода звена коэффициент усиления имеет размерность [c].
Приведенная с точки зрения статики классификация линейных динамических звеньев является довольно укрупненной. Более детальная, с позиций динамики, классификация звеньев осуществляется по виду дифференциального уравнения или передаточной функции звена 
, где 
-изображения по Лапласу соответственно выходного и входного сигналов звена. Звено, описываемое дифференциальным уравнением не выше второго порядка, называют типовым или элементарным звеном.
Динамические свойства и параметры звена можно определить по его временным и частотным характеристикам, которые находятся экспериментальным или расчетным путем.
