Одной из важных задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по эмпирическому распределению, представляющему вариационный ряд.
Для решения этой задачи необходимо определить вид и параметры закона распределения.
Предположение о виде закона распределения может быть выдвинуто, исходя из теоретических предпосылок (например, выполнение условий центральной предельной теоремы может свидетельствовать о возможности нормального закона распределения случайной величины), опыта аналогичных исследований и, наконец, на основании графического изображения эмпирического распределения.
Параметры распределения, как правило, неизвестны, поэтому их заменяют «наилучшими» оценками по выборке.
Как бы хорошо не был подобран теоретический закон распределения, между эмпирическим и теоретическим распределением неизбежны расхождения. Естественно возникает вопрос: объясняются ли эти расхождения только случайными причинами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что теоретический закон распределения подобран неудачно? Для ответа на поставленный и аналогичный вопросы в математической статистике разработаны методы проверки статических гипотез.
Статической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения.
Проверяемую гипотезу обычно называют нулевой и обозначают Н0. Например, гипотеза Н0: случайная величина Х распределена по нормальному закону с параметрами а=5, 2=2.
Правило, по которому гипотеза Н0 отвергается или принимается (точнее не отвергается), называется статическим критерием. Статические критерии, служащие для проверки гипотез о виде закона распределения, называются критериями согласия.
Вероятность допустить ошибку, а именно: отвергнуть гипотезу Н0, когда она верна, называется уровнем значимости критерия.
Пусть необходимо проверить нулевую гипотезу Н0 о том, что исследуемая случайная величина Х подчиняется определенному закону распределения. Для проверки гипотезы Н0 выбирают некоторую случайную величину U, характеризующую степень расхождения теоретического и эмпирического распределений, закон распределения которой при достаточно больших n известен и практически не зависит от закона распределения случайной величины Х.
Зная закон распределения U можно найти вероятность того, что U приняла значение не меньшее, чем фактически наблюдаемое в опыте u, т.е. Uu. Если вероятность P(Uu)= мала, то это означает в соответствии с принципом практической уверенности, что такие, как в опыте u, и большие отклонения практически невозможны. В этом случае гипотезу Н0 отвергают. Если же вероятность P(Uu)= не мала, т.е. расхождение между эмпирическим и теоретическим распределением не существенно, то гипотезу Н0 можно считать правдоподобной или, по крайней мере, не противоречащей опытным данным.
В наиболее используемом на практике критерии 2 Пирсона в качестве меры расхождения U берется величина 2 («хи-квадрат»).
(*)
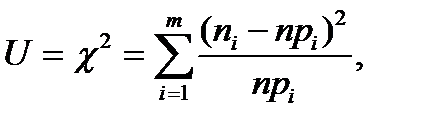где 
– эмпирические (опытные) частоты случайной величины Х;
-теоретические частоты, представляющие произведение числа наблюдений n на вероятность pi, рассчитанные по предполагаемому теоретическому распределению.
Доказано, что выборочная характеристика или, как ее еще называют, статистика 2 (*) при n имеет 2 –распределение с 
степенями свободы,
где m –число интервалов эмпирического распределения (вариационного ряда);
s –число параметров теоретического распределения, определяемых по опытным данным (например, в случае нормального закона распределения число оцениваемых по выборке параметров s=2).
Схема применения критерия 2 сводится к следующему:
1.Определяемая мера расхождения эмпирических и теоретических частот 2 по (*).
2.Для выбранного уровня значимости по таблице 2 –распределения находят критическое значение 2,, при числе степеней свободы .
3.Если фактически наблюдаемое значение 2 больше критического, т.е. 2 >2,, гипотеза Н0 отвергается, если 2 
2,, гипотеза Н0 не противоречит опытным данным.
В таблице 1 приводятся наиболее часто используемые на практике значения 2 –критерия Пирсона.
Таблица 6.6.5. Некоторые значения 20,05; k критерия Пирсона
| Число степеней свободы k | |||||||||||||||||
| 20,05; k | 3,84 | 5,99 | 7,82 | 9,49 | 11,1 | 12,6 | 14,1 | 15,5 | 16,9 | 18,3 | |||||||
Замечание 6.6.1. Если в таблице 2 –распределения приводятся вероятности P(2 >2,), то гипотеза Н0 отвергается, если вероятность P(2 >2,) меньше выбранного уровня значимости и –принимается в противном случае.
Замечание 6.6.2. Критерий 2 Пирсона дает удовлетворительные результаты, если в каждом группировочном интервале достаточное число наблюдений ni; если в каком-нибудь интервале число наблюдений меньше, например, 5, имеет смысл объединить соседние интервалы с тем, чтобы в объединенных интервалах ni,
было меньше 5. Пи этом при вычислении числа степеней свободы к в качестве m берется соответственно уменьшенное число интервалов.
Пример 6.6.5Получено следующее распределение 100 рабочих цеха по выработке в отчетном году (в процентах к предыдущему году):
Таблица 6.6.6
| Выработка в отчетном году (в % к предыдущему) | 94-104 | 104-114 | 114-124 | 124 -134 | 134 -144 | 
| |||
| Количество рабочих | |||||||||
На уровне значимости 
проверить гипотезу о нормальном распределении случайно величины Х – выработки рабочих – с помощью критерия 
Пирсона.
Решение. Параметры теоретического нормального закона распределения а и 
, являющиеся соответственно математическим ожиданием и дисперсией случайно величины Х, неизвестны, поэтому заменяем их «наилучшими» оценками по выборке – несмещенными и состоятельными оценками соответственно выборочной средней х и «исправленной» выборочной дисперсии 
. Так как число наблюдений n = 100 достаточно велико, то вместо исправленной 
можно взять «обычную» выборочную дисперсию 
. По данному в условии распределению были вычислены 
Для расчета вероятностей р1 попадания случайно величины Х в интервале 
, где i = 1,2,...,m, используем функцию Лапласа Ф(х) в соответствии со свойством нормального распределения:
Например,
и соответствующая первому теоретическая частота np1=100*0,49=4,9. Аналогично вычисляем частоты np1 в других интервалах (i = 1, 2,..., m). Для определения статистики 
удобно составить таблицу:
Таблица 6.6.7
| № № i | Интервал [хi, xi+1] | Эмпирические частоты ni | Вероятности pi | Теоретические частоты npi | (ni - npi)2 | 
| |
| 94-104 | 0.049 | 4.9 | 1.21 | 0.247 | |||
| 104-114 | 0.239 | 23.9 | 15.21 | 0.636 | |||
| 114-124 | 0.404 | 40.4 | 21.16 | 0.524 | |||
| 124-134 | 0.248 | 24.8 | 0.64 | 0.026 | |||
| 134-144 | 0.053 | 5.3 | 0.09 | 0.017 | |||
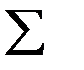
| 0.993 | 99.3 | - | 1.45 | |||
Итак, фактически наблюдаемое значение статистики 
. Так как число интервалов m = 5, а нормальный закон распределения определяется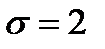 
параметрами (которые мы оценили по выборке), то число степеней свободы 
. Соответствующее критическое значение статистики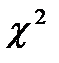 
по таблице 9, 
. Так как 
, то гипотеза о выбранном теоретическом нормальном законе распределения с параметрами а = 119,2 и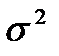 
= 87,96 согласуется с опытными данными.
Изобразить эмпирические распределения можно, например, ступенчатой фигурой, состоящей из прямоугольников с основания
ми, равными величинам интервалов Δхi = хi+1 - хi, и высотами, равными частностям 
(или частотам n1) этих интервалов, называемой гистограммой. При построении нормальной кривой для каждого интервала по оси ординат откладываем соответствующие вероятности рi (теоретические частоты npi). Выполнив чертеж, можно увидеть, что нормальная кривая теоретического распределения достаточно хорошо «выравнивает» гистограмму эмпирического распределения.
Замечание 6.6.3 Если при проверке гипотезы используется таблица вероятностей 
, то необходимо найти вероятность Р для вычисленного значения 
при числе степеней свободы к = 2. Непосредственно такого значения в таблице нет. Но (при к = 2) для ближайших соседних значений , равных 1 и 2, вероятность Р соответственно равна 0,3679 и 0, 06065. Таким образом, и без интерполяции ясно, что вероятность Р больше заданного уровня значимости 
, т.е. P > 0,05, следовательно, в соответствии с замечанием 1, нулевая гипотеза Н0 согласуется с опытными данными.
Замечание 2. Если в исходном распределении частоты некоторых интервалов меньше 5, то в соответствии с замечанием 2 их целесообразно объединить с соседними.
Предположим, что в распределении рабочих в последнем интервале выработки 134 Х 144 (%) частота (количество рабочих) равняется не 5 (как в рассмотренном примере), а например, 2. В этом случае последний интервал объединяем с предыдущим, полагая при вычислении его частоту равной 24 + 2 = 26. В этом случае для решения вопроса о справедливости гипотезы Н 0 вычисленное значение следовало сравнивать с критическим значением при числе степеней свободы k = m –s –1 = 4 – 2 – 1 = 1, уменьшенным на единицу за счет сокращения числа интервалов, т.е.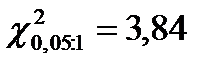 
.
Контрольные работы
Контрольная работа №5
Векторный анализ
Задача 1. Найти векторные линии в векторном поле 
.
1.1.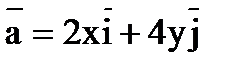 
Задача 2. Найти поток векторного поля 
через часть плоскости Р, расположенную в первом октанте (нормаль образует острый угол с осью Dz).
| 
|
| 
|
| 
|
| 
|
| 
|
Задача 3. Найти поток векторного поля 
через замкнутую поверхность S (нормаль внешняя). 
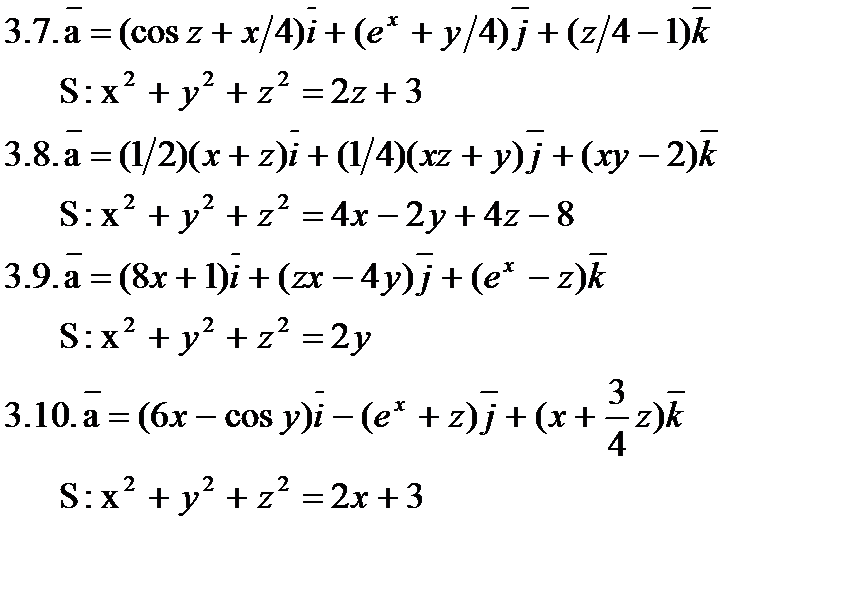
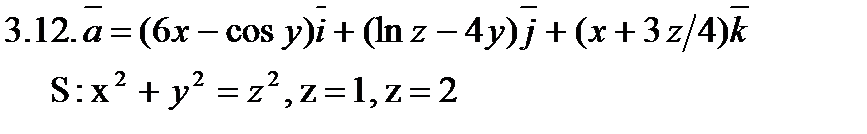
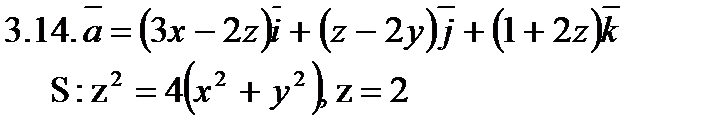
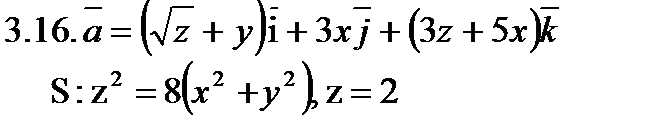
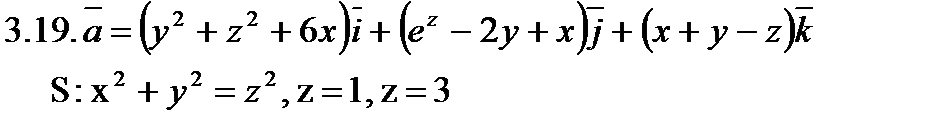
Задача 4. Найти работу силы 
при перемещении вдоль отрезка MN от точки M к точке N.
Числовые ряды
5.Доказать непосредственно (по определению) сходимость следующих рядов и вычислить их суммы:
5.1. 1 – ½ + 1/4-1/8+…+(-1)n-1/2n-1+…
5.2. (1/2+1/3)+(1/22+1/32)+…(1/2n+1/3n)+…
5.3. ½+3/22+5/23+…+2n-1/2n+…
5.4. 1/1*2+1/2*3+…+1/n(n-1)+…
5.5. 1/1*4+1/4*7+…+1/(3n-2)*(3n+1)+…
5.6. 
5.7. 
5.8. 
5.9. 
5.10. 
5.11. 
5.12. 
5.13. 
5.14. 
5.15. 
5.16. 
5.17. 
5.18. 
5.19. 
5.20. 
6. Исследовать на сходимость числовые ряды
6.1.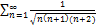 
6.2. 
6.3.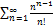 
6.4. 
6.5.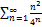 
6.6. 
6.7. 
6.8. 
6.9. 
6.10. 
)n
6.11. 
6.12. 
6.13. 
6.14. 
6.15. 
)n
6.16. 
6.17. 
n
6.18. 
6.19. 
6.20. 
7.Исследуйте на сходимость следующие ряды:
7.1. 
7.2. 
7.3. 
7.4. 
7.5. 
7.6.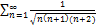
7.7.
7.8. 
7.9. 
7.10. 
7.11. 
7.12. 
7.13. 
7.14. 
7.15. 
7.16. 
7.17. 
7.18.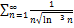 
7.19. 
7.20.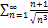 
8.Исследовать на абсолютную и условную сходимость следующие знакочередующиеся ряды:
8.1. 
8.2.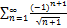 
8.3. 
8.4.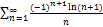 
8.5. 
8.6.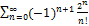 
8.7. 
8.8. 
8.9. 
8.10.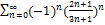 
8.11. 
8.12. 
8.13. 
8.14. 
8.15. 
8.16. 
8.17.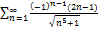 
8.18. 
8.19.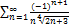 
8.20. 
9.Определить область сходимости функционального ряда и исследовать на сходимость на границе области сходимости следующие функциональные ряды:
9.1. 
9.2. 
9.3.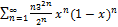 
9.4.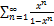 
9.5. 
9.6. 
9.7. 
9.8. 
9.9. 
9.10. 
9.11.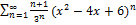 
9.12. 
9.13.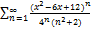 
9.14. 
9.15. 
9.16. 
9.17. 
9.18.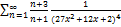 
9.19.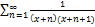 
9.20. 
10. Найти радиус и интервал сходимости. Исследовать на сходимость на концах интервала:
10.1. 
(
10.2.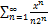 
10.3. 
10.4. 
10.5. 
10.6. 
10.7. 
10.8. 
10.9. 
10.10. 
10.11. 
10.12.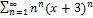 
10.13. 
10.14. 
10.15. 
10.16. 
10.17. 
10.18. 
10.19. 
10.20. 
11. Разложить следующие функции в ряд Маклорена. Найти их интервал сходимости:
11.1. y=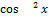 
11.2. y= 
11.3. y= 
x
11.4. y=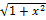 
11.5. y=(x-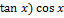 
11.6. y=x 
11.7. y= 
11.8. y= 
11.9. y= 
11.10. y= 
11.11. y= 
11.12. y= (1+X) 
11.13. y= 
11.14. y= (1+ 
11.15. y= 
11.16. y= 
x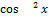
11.17. y= 
11.18. y= 
11.19. y= (3+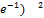 
11.20. y= (
12. Вычислить интеграл с точностью до 0,001:
12.1. 
12.2. 
12.3. 
12.4.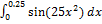 
12.5. 
12.6. 
12.7. 
12.8. 
12.9. 
12.10. 
12.11. 
12.12. 
12.13. 
12.14. 
12.15. 
12.16. 
) 
12.17. 
12.18. 
12.19. 
12.20. 
13. Разложить в ряд Фурье функции с периодом 2π:
13.1. ƒ(x)= π2-x2; x€ 
13.2. ƒ(x)= 
x€
13.3. ƒ(x)= 
x€
13.4. ƒ(x)= 
-π 
0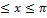 
13.5. ƒ(x)= 
x€
13.6. ƒ(x)= 
x€
13.7. ƒ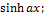(x)= 
x€
13.8. ƒ(x)= 
; x€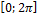 
13.9. ƒ(x)=x 
x€
13.10. ƒ(x)=x 
x€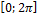
13.11. ƒ(x)= 
x€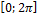
13.12. ƒ(x)= 
-π 
0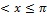 
13.13. ƒ(x)= 
x€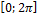
13.14. ƒ(x)= 
x€
13.15. ƒ(x)= 
x€
13.16. ƒ(x)= 
x€
13.17. ƒ(x)= 
x€
13.18. ƒ(x)= x- x€
13.19. ƒ(x)= 
x€
13.20. ƒ(x)= 
x€
Комплексные переменные
Задача 14.Найти модуль и аргумент комплексного числа: 
Задача 15. Вычислить 
Задача 16. Найти все значения
