13.8 F(x)= 
13.9 F(x)= 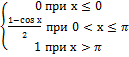
13.10 F(x)= 
13.11 F(x)= 
13.12 F(x)= 
13.13 F(x)= 
13.14 F(x)= 
13.15 F(x)= 
13.16 F(x)= 
13.17 F(x)= 
13.18 F(x)= 
13.19 F(x)= 
13.20 F(x)= 
Задание 14
1) постоянную распределения а;
2) функцию распределения Fx);
3) математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины Х;
4) верочтность попадания случайной величины в интервал (-2;1).
14.1 f(x)= 
14.2 f(x)= 
14.3 f(x)= 
14.4 f(x)= 
14.5 f(x)= 
14.6 f(x)= 
14.7 f(x)= 
14.8 f(x)= 
14.9 f(x)= 
14.10 f(x)= 
14.11 f(x)= 
14.12 f(x)= 
14.13 f(x)= 
14.14 f(x)= 
14.15 f(x)= 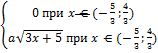
14.16 f(x)= 
14.17 f(x)= 
14.18 f(x)= 
14.19 f(x)= 
14.20 f(x)= 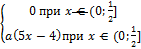
Контрольная работа №7
Задание 1
Даны следующие дискретные распределения: а) проданной мужской обуви по размеру (таблица 1); б) ткачей фабрики по числу обслуживаемых ими станков (таблица 2). Для каждого из их этих распределений: вычислить среднюю арифметическую дисперсию, среднее квадратическое отклонение; найти эмпирическую функцию распределения.
1.1. таблица 1
| Размер обуви | Число пар |
Итого 117
1.2. Таблица 2
| Число станков | Число ткачей |
Итого 446
Даны следующие непрерывные распределения: а) рабочих по времени, затраченному на обработку одной детали (таблица 3); б) нитей пряжи по крепости (таблица 4). Для каждого из этих распределений: вычислить среднюю арифметическую, дисперсию и среднее квадратическое отклонение; найти эмпирическую функцию распределения.
1.3 Таблица 3
| Время на обработку одной детали, мин | Число рабочих | Время на обработку одной детали, мин | Число рабочих |
| 4.0-4.5 | 6.5-7 | ||
| 4.5-5 | 7.0-7.5 | ||
| 5.0-5.5 | 7.5-8.0 | ||
| 5.5-6.0 | 8.0-8.5 | ||
| 6.0-6.5 |
Итого 500
1.4 Таблица 4
| Крепость нити, г | Число нитей | Крепость нити, г | Число нитей, г |
| 200-250 | 350-400 | ||
| 250-300 | 400-450 | ||
| 300-350 |
Итого 250
1.5. Распределение квартир жилого дома по суточному потреблению эл. Энергии (по дням недели) приведено в таблице 5. Вычислить групповые и общие средние и дисперсии этого распределения, затем проверить результаты, применив правила сложения средних арифметических и дисперсий.
| Потребление эл. Энергии, кВт*ч | Количество квартир | |||||||
| Пн. | Вт. | Ср. | Чт. | Пт. | Сб. | Вс. | Итого | |
| 0,75-1,25 | - | - | - | |||||
| 1,25-1,75 | ||||||||
| 1,75-2,25 | ||||||||
| 2,25-2,75 | ||||||||
| 2,75-3,25 | ||||||||
| 3,25-3,75 | ||||||||
| 3,75-4,25 | ||||||||
| 4,25-4,75 | ||||||||
| 4,75-5,25 | ||||||||
| 5,25-5,75 | - | |||||||
| 5,75-6,25 | - | - | - | - | ||||
| 6,25-6,75 | - | - | - | - | - | |||
| Итого |
1.6 В результате выборки получены числа -5,1,-3,-2,0,0,3,-3,-2,0,1,2,0,0. Постройте график эмпирической функции распределения и гистограмму; вычислите среднюю арифметическую и дисперсию.
1.7 Для выборки: 2,-1,2,-1,-4,5,2,2,-1,5 постройте эмпирическую функцию распределения и гистограмму; вычислить среднюю арифметическую, дисперсию.
1.8 В цехе работаю четыре станка, причем вероятность остановки в течении часа для каждого из них равна 0,8. Построить полигон распределения вероятности числа станков, остановившихся в течение данного часа.
1.9 Через каждый час измерялось напряжение тока в электросети. При этом получены следующие значения:
Таблица6
Постройте эмпирическую функцию распределения, гистограмму; вычислите среднюю арифметическую и дисперсию. 1.10 На приемных экзаменах выборка среди абитуриентов дала следующие выбранные ими баллы:
Таблица 7
Постройте эмпирическую функцию распределения, гистограмму; вычислите среднюю арифметическую и дисперсию.
В задачах 1.11-1.20 даны статические ряды. Вычислите те же задания, что и в задаче 1.10
1.11 Таблица 8
| Границы интервалов | 85-105 | 105-125 | 125-145 | 145-165 | 165-185 | 185-205 | 205-225 |
| Частота |
1.12 Таблица 9
| Границы интервалов | 60-64 | 64-68 | 68-72 | 72-76 | 76-80 | 80-84 |
| частота |
1.13 Таблица 10
| Границы интервалов | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 |
| Частота |
1.14 Таблица 11
| Границы интервалов | 10-14 | 14-18 | 18-22 | 22-26 | 26-30 | 30-34 |
| Частота |
1.15 Таблица 12
| Границы интервалов | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 |
| Частота |
1.16 Таблица 13
| Границы интервалов | 60-65 | 65-70 | 70-75 | 75-80 | 80-85 | |
| Частота |
1.17 Таблица 14
| Границы интервалов | 12-16 | 16-20 | 20-24 | 24-28 | 28-32 | 32-36 |
| Частота |
1.18 Таблица 15
| Границы интервалов | 100-110 | 110-120 | 120-130 | 130-140 | 140-150 | 150-160 |
| Частота |
1.19 Таблица 16
| Границы интервалов | 200-220 | 220-240 | 240-260 | 260-280 | 280-320 | 320-340 |
| Частота |
1.20 Таблица 17
| Границы интервалов | 73-75 | 75-77 | 77-79 | 79-81 | 81-83 | 83-85 |
| Частота |
Задание 2
2.1 Для изучения мощности тракторных парков было обследовано 250 парков из 2500, отобранных по схеме собственно- случайной выборки. Их распределение по мощности тракторных парков дано в таблице 18:
Таблица 18
| Мощности, Тыс.л.с | 0,6- 0,1 | 1,0- 1,4 | 1,4-1 | 1,8- 2,2 | 2,2- | 2,6-3,0 | 3,0-3,4 | Итого |
| Число парков | 2,6 |
Найти границы, в которых с вероятностью 0,9876 заключена средняя мощность тракторного парка для всей совокупности парков, если выборка: а) повторная; б) бесповторная
2.2. Испытывалась чувствительность второго канала 100 телевизоров из партии 2000шт., изготовленных одним заводом. Получены следующие данные:
Таблица 19
| Чувствительность канала МТВ | 475-525 | 525-275 | 575-625 | 625-675 | 675-725 | Итого |
| Число телевизоров |
Определить вероятность того, что средняя чувствительность второго канала во всей партии телевизоров отличается от полученной средней чувствительности телевизоров в выборке не более чем на 10 МТВ по абсолютной величине. Задачу решить для повторной и бесповторной выборок.
2.3 Чтобы установить содержание золы на очень большой партии каменного угля, было взято 500 проб. Результаты анализа приведены в таблице 20:
Таблица 20
| Содержание Золы, % | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | Итого |
| Число проб |
2.4 В детском спорткомплексе занимаются 2000 школьников. Для определения их среднего возраста случайным бесповторным отбором взята информация у 100 детей. Результаты выборки показаны в таблице 21:
Таблица 21
| Возраст, Лет | 6-8 | 8-10 | 10-12 | 12-14 | 14-16 | 16-18 | Итого |
| Кол-во Опрош. |
Найти: а) границы, в которых с вероятностью 0,97 заключен средний возраст школьников, посещающих этот спорткомплекс; б) вероятность того, что доля школьников, старше 12 лет, среди всех посетителей отличаются от выборочной доли таких школьников не более чем на 0,12 (по абсолютной величине).
2.5 Для определения средней мощности моторов по схеме бесповторного случайного отбора было обследовано 100 моторов из 1000, имеющихся на заводе, результаты которого приведены в таблице 22:
Таблица 22
| Мощность моторов, кВТ | 3,7-3,8 | 3,8-3,9 | 3,9-4,0 | 4,0-4,1 | 4,1-4,2 | 4,2-4,3 | Итого |
| Кол-во моторов |
Найти: а) вероятность того, что средняя мощность всех моторов отличается от средней выборочной не более чем на 0,01 по абсолютной величине; б) границы, в которых с вероятностью 0,8064 заключена средняя мощность моторов во всей партии.
2.6 Из партии, содержащей 4000 деталей, было отобрано по схеме собственно случайной бесповторной выборки 400 деталей. Распределение этих деталей по длине дано в таблице 23:
Таблица 23
| Длина, мм | 3,2-3,3 | 3,3-3,4 | 3,4-3,5 | 3,5-3,6 | 3,6-3,7 | Итого |
| Число деталей |
Требуется найти: а) границы, в которых с вероятностью 0,9973 заключена средняя длина деталей во всей партии; б) вероятность того, что доля деталей во всей партии, длина которых составляет от 3,4 до 3,6 мм, отличается от доли таких деталей в выборке не более чем на 0,01 по абсолютной величине.
2.7 Данные о продолжительности 150 телефонных разговоров, отобранных по схеме собственно случайной повторной выборки, представлены в таблице 24:
| Продол- жительность разговора,мин | 1,5-2,5 | 2,5-3,5 | 3,5-4,5 | 4,5-5,5 | 5,5-6,5 | 6,5-7,5 | 7,5-8,5 | 8,5-9,5 | 9,5-10,5 | Итого |
| Число разговоров |
Таблица 24
Необходимо: а) найти границы, в которых с вероятностью 0,9973 заключена средняя продолжительность телефонного разговора в генеральной совокупности; б) найти вероятность того, что доля телефонных разговоров, продолжительность которых превышает 8,5 мин. По данным выборки, отличается от доли таких разговоров в генеральной совокупности не более чем на 0,05 по абсолютной величине.
2.8 Для анализа выполнения плана реализации услуг в 5000 предприятиях бытового обслуживания в регионе было проверено по схеме случайной бесповторной выборки 200 предприятий. Результаты проверки даны в таблице 25:
Таблица 25
| Выполнение плана,% | 90-93 | 93-96 | 96-99 | 99-102 | 102-105 | 105-108 | Итого |
| Число предприятий |
Найти: а) вероятность того, что средний процент выполнения плана всеми предприятиями отличается от среднего выборочного не более чем на 0,5% по абсолютной величине; б) границы доли предприятий, которые выполнили план не более чем на 99% с вероятностью 0,9973.
2.9 Для определения средней стоимости пошива одной вещи в ателье из 10000 заказов по схеме собственно случайной бесповторной выборки было отобрано 500 квитанций, распределение суммы заказа на которых дано в таблице 26:
Таблица 26
| Стоимость заказа, руб | 0-100 | 100-200 | 200-300 | 300-400 | 400-500 | 500-600 | Более 600 | Итого |
| Число квитанций |
Найти: а) границы, в которых с вероятностью 0,899 заключена средняя стоимость заказа во всей партии; б) вероятность того, что доля всех заказов стоимостью от 200 до 500 руб. отличается от доли их в выборке не более чем на 0,05 (по абсолютной величине).
2.10 По схеме собственной случайной бесповторной выборки было отобрано 100 студенток из 1500 и получены следующие данные о их росте:
Таблица 27
| Рост, см | 154-158 | 158-162 | 162-166 | 166-167 | 170-174 | 174-178 | Итого |
| Число студенток |
Найти: а) граница, в которых с вероятность 0,95 заключен средний рост студенток во всей совокупности; б) вероятность того, что доля студенток, рост которых не менее 170 см во всей совокупности, отличается от выборочной доли таких студенток не более чем на 0,05.
2.11 В художественной школе занимаются 2000 школьников. Для определения их среднего возраста случайным бесповторным отбором взята информация у 80 детей. Результаты выборки показаны в таблице 28:
Таблица 28
| Возраст, Лет | 6-8 | 8-10 | 10-12 | 12-14 | 14-16 | 16-18 | Итого |
| Кол-во Опрош. |
Найти: а) границы, в которых с вероятностью 0,97 заключен средний возраст школьников, посещающих этот спорткомплекс; б) вероятность того, что доля школьников, старше 12 лет, среди всех посетителей отличаются от выборочной доли таких школьников не более чем на 0,12 (по абсолютной величине).
2.12 Испытывалась чувствительность первого канала 100 телевизоров из партии 2500шт., изготовленных одним заводом. Получены следующие данные:
Таблица 29
| Чувствительность канала МТВ | 475-525 | 525-275 | 575-625 | 625-675 | 675-725 | Итого |
| Число телевизоров |
Определить вероятность того, что средняя чувствительность первого канала во всей партии телевизоров отличается от полученной средней чувствительности телевизоров в выборке не более чем на 10 МТВ по абсолютной величине. Задачу решить для повторной и бесповторной выборок.
2.13 По схеме собственной случайной бесповторной выборки было отобрано 100 девочек из 1500 и получены следующие данные о их росте:
Таблица 30
| Рост, см | 160-163 | 163-166 | 166-169 | 169-172 | 172-175 | 175-178 | Итого |
| Число студенток |
Найти: а) граница, в которых с вероятность 0,95 заключен средний рост студенток во всей совокупности; б) вероятность того, что доля студенток, рост которых не менее 172 см во всей совокупности, отличается от выборочной доли таких студенток не более чем на 0,05.
2.14 Для определения средней мощности компьютера по схеме бесповторного случайного отбора было обследовано 100 моторов из 1000, имеющихся на заводе, результаты которого приведены в таблице 31:
Таблица 31
| Мощность компьютеров, кВТ | 3,7-3,8 | 3,8-3,9 | 3,9-4,0 | 4,0-4,1 | 4,1-4,2 | 4,2-4,3 | Итого |
| Кол-во моторов |
Найти: а) вероятность того, что средняя мощность всех моторов отличается от средней выборочной не более чем на 0,01 по абсолютной величине; б) границы, в которых с вероятностью 0,8064 заключена средняя мощность компьютеров во всей партии.
2.15 Из партии, содержащей 4000 линеек, было отобрано по схеме собственно случайной бесповторной выборки 400 линеек. Распределение этих деталей по длине дано в таблице 32:
Таблица 32
| Длина, мм | 3,2-3,3 | 3,3-3,4 | 3,4-3,5 | 3,5-3,6 | 3,6-3,7 | Итого |
| Число линеек |
Требуется найти: а) границы, в которых с вероятностью 0,9973 заключена средняя длина линеек во всей партии; б) вероятность того, что доля линеек во всей партии, длина которых составляет от 3,4 до 3,6 мм, отличается от доли таких линеек в выборке не более чем на 0,01 по абсолютной величине.
2.16 Чтобы установить содержание соли в очень большом количестве воды, было взято 500 проб. Результаты анализа приведены в таблице 33:
Таблица 33
| Содержание соли, % | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | Итого |
| Число проб |
2.17 Чтобы установить содержание витамина в очень большой партии продуктов, было взято
500 проб. Результаты анализа приведены в таблице 34:
Таблица 34
| Содержание Витамина В, % | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | Итого |
| Число проб |
2.18. По схеме собственной случайной бесповторной выборки было отобрано 100 детей из 1500 и получены следующие данные о их росте:
Таблица 35
| Рост, см | 110-115 | 115-120 | 120-125 | 125-130 | 130-135 | 135-140 | Итого |
| Число Детей |
Найти: а) граница, в которых с вероятность 0,95 заключен средний рост студенток во всей совокупности; б) вероятность того, что доля детей, рост которых не менее 135 см во всей совокупности, отличается от выборочной доли таких студенток не более чем на 0,05.
2.19. По схеме собственной случайной бесповторной выборки было отобрано 100 людей из 1500 и получены следующие данные о их возрасте:
Таблица 36
| Возраст, лет | 35-45 | 45-55 | 55-65 | 65-75 | 75-85 | 85-95 | Итого |
| Число людей |
Найти: а) граница, в которых с вероятность 0,95 заключен средний возраст людей во всей совокупности; б) вероятность того, что доля людей, возраст которых не менее 65 лет во всей совокупности, отличается от выборочной доли таких студенток не более чем на 0,05.
2.20 Таблица 37
| Мощности, Тыс.л.с | 0,6- 0,1 | 1,0- 1,4 | 1,4-1 | 1,8- 2,2 | 2,2- | 2,6-3,0 | 3,0-3,4 | Итого |
| Число парков | 2,6 |
Для изучения мощности машинных парков было обследовано 250 парков из 2500, отобранных по схеме собственно- случайной выборки. Их распределение по мощности машинных парков дано в таблице 37:
Найти границы, в которых с вероятностью 0,9876 заключена средняя мощность машинного парка для всей совокупности парков, если выборка: а) повторная; б) бесповторная
Задание 3
3.1 Используя χ2 – критерий Пирсона на основе выборочных данных задачи № 2 при уровне значимости α=0,05, проверить гипотезу о том, что случайная Х – мощность тракторного парка – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.






