Как известно из теории вероятностей, функция распределения вероятностей случайной величины «X», определяемая соотношением 
является универсальной формой задания закона распределения, как для дискретных, так и для случайных непрерывных величин.
Поэтому, используя теорему сложения вероятностей и заменяя теоретические вероятности pi на их оценки 
, мы получаем следующую эмпирическую функцию распределения Fn(x) для случая дискретной исследуемой случайной величины:
при 
| ||
| 1 | при 
| |
| 1+2 | при 
| |
| ……… | ||
| при 
|
В случае непрерывной исследуемой величины Х при извлечении выборки 
для случайного события 
мы опять имеем классическую схему Бернулли, поэтому теоретическая вероятность события «Аi», определяемая в теории вероятностей как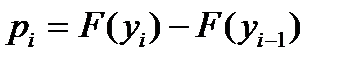 
, оценивается относительной частотой 
попадания точки выборки в i -й класс. Припишем эту вероятность середине i -го класса, т.е значению 
,
далее строим эмпирическую функцию так же, как и для случая дискретной случайной величины, в результате мы получим:
при 
| ||
| 1 | при 
| |
| 1+2 | при 
| |
| ……… | ||
|
| при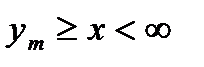 
|
Полученные таким образом функции являются оценкой теоретической функции распределения F(x); из теоремы Бернулли следует, что Fn(x) сходится по вероятности при объеме выборки n к F(x), т.е. для любого положительного числа и любого числа -<x<+ 
.
при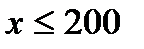 
| ||
| 1/10 | при 
| |
| 3/10 | при 
| |
| 5/10 | при 
| |
| 7/10 | при 
| |
| 8/10 | при 
| |
| 9/10 | при 
| |
при 
|
Пример 6.6.1 Результаты проверки 10 ти однотипных приборов на длительность работы представлены следующей таблицей.
Таблица 6.6.2
| i(номер прибора) | ||||||||||
| x1(время работы в часах) |
Статическое распределение частот
Таблица 6.6.3
| x1 | |||||||
| n1 | |||||||
| 1 | 1/10 | 2/10 | 2/10 | 2/10 | 1/10 | 1/10 | 1/10 |
Эмпирическая функция F*(x).
Чтобы найти значение F*(x), нужно подсчитать число вариант, меньших х и разделить на общее число вариант:
График функций F*(x)
| 0,9 | ||||||||
| 0,8 | ||||||||
| 0,7 | ||||||||
| 0,6 | ||||||||
| 0,5 | ||||||||
| 0,4 | ||||||||
| 0,3 | ||||||||
| 0,2 | ||||||||
| 0,1 | ||||||||
0 100 200 300 400 500 600 700 800
Рис. 6.6.1.
Гистограмма
На практике имеет распространение и другое графическое представление выборки, известное под названием гистограммы выборки.
Предварительно выборка подвергается группировке. Для этого весь интервал числовой оси, в который попадают значения выборки 
, разбивают на несколько частичных интервалов (обычно 10-20) длиною h и находят для каждого частичного интервала ni-сумму частот вариант, попавших в i -тый интервал. Над каждым из интервалов, как на основании, строится прямоугольник высотой ni/h (плотность частоты).
