В этих темах условные обозначения Х, а, P будем понимать точно так, как они были использованы и разъяснены в предыдущей теме, а 
-общее обозначение для средних квадратических ошибок x, `x, , `, которые вычисляются по формулам (6.6.1).
Доверительная вероятность P для заданных предельной ошибке и средней квадратической ошибке (в зависимости от вида и цели выборки это будет x, `x, , `) вычисляется по формуле (6.6.1)
(6.6.1)
Средняя квадратическая ошибка (т.е. x, или `x, или , или `) вычисляется по одной из следующих формул:
| Выборка Приказ | Повторная | Бесповторная |
| для средней | (а)
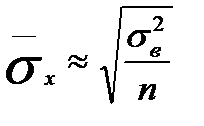
| (б)
 (6.6.3)
|
| для доли | (в)
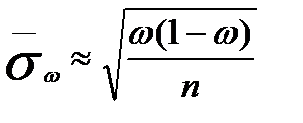
| (г)
|
Иногда для удобства вычислений выражение 
обозначается одной буквой t.
. (6.6.2)
Откуда 
.
Объем выборки n при фиксированных предельной ошибке и доверительной вероятности P вычисляется в зависимости от вида и цели выборки по одной из следующих четырех формул:
таблица 6.6.4
| Выборка Приказ | Повторная | Бесповторная |
| Для Средней | (а)
| (б)
 (6.6.4)
|
| Для Доли | (в)
| (г)
|
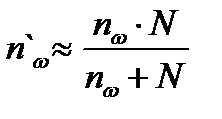
Рассмотрим решение трех типов задач.
I.Даны P, n и X; требуется определить предельную ошибку выборки или доверительные границы 
и 
.
Решение: 1.По заданной величине P с помощью таблицы значений функции Ф(t) находим аргумент t (выполняя, если требуется, интерполирование).
2.Вычисляем среднюю квадратическую ошибку выборки по одной из формул (6.6.1).
3.Из выражения (6.6.2) находим предельную ошибку выборки
.
4.Определяем доверительные границы и .
II.Дана предельная ошибка выборки , n и X; требуется определить доверительную вероятность P.
Решение: 1.Вычисляем среднюю квадратическую ошибку выборки по одной из формул (6.6.1).
2.Вычисляем аргумент t по формуле (6.6.2);
3.Для найденного значения t определяем по таблице значение функции Лапласа Ф(t)=P.
III.Даны P, и X. Требуется определить необходимый объем выборки n.
Решение: 1.По заданному значению доверительной вероятности P= Ф(t) определяем по таблице приложений значение t.
2.Вычисляем требуемый объем выборки n
Пример 6.6.2 По схеме собственно случайной бесповоротной выборки из общего числа 400 стальных проволок были отобраны 100 проволок и проведены испытания их на прочность.
Результаты испытаний приведены в следующей таблице:
таблица 6.6.4
| Разрывное усилие, Н/м | 40-42 | 42-44 | 44-46 | 46-48 | 48-50 | Итого |
| Количество проволок |
Найти: 1) вероятность того, что среднее разрывное усилие всех 400 проволок отличается от среднего разрывного усилия проволок в выборке не более чем на 0,31 (по абсолютной величине); 2) границы, в которых с вероятностью 0,9975 заключено среднее разрывное усилие проволок всей партии; 3) объем выборки, для которой доверительные границы с предельной ошибкой =0,42 имели бы место с доверительной вероятностью P=0,9961.
Решение. 1.Прежде всего нужно подсчитать выборочную среднюю и выборочную дисперсию данной выборки. Согласно этим вычислениям 
подсчитаем теперь среднюю квадратическую ошибку выборочной средней, учитывая, что по условию выборка бесповоротная, а оценивает-
ся генеральная средняя:
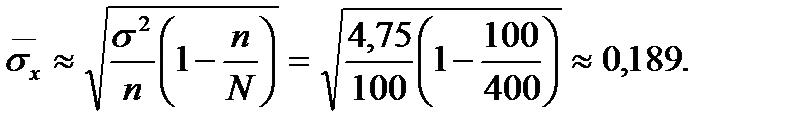
Чтобы получить ответ на первый вопрос условия, подставляем найденные значения в формулу (6.6.1):
2.Сначала по таблице значений функции Ф(x) найдем такое значение аргумента t, для которого Ф(t)=0,9975. Это t3,02. Тогда предельная ошибка выборки:
3,020,1890,57 (Н/мм2).
Поэтому доверительные границы будут
3.Для получения ответа на третий вопрос условия, нужно применить формулы (6.6.3). Предварительно по таблице значений функции Ф(x) найдем значение аргумента t, при котором Ф(t)=0,9961. Получаем t=2,89. По условию выборка бесповоротная, а оценивается генеральная средняя. Подсчитаем сначала по формуле (4) объем повторной выборке при тех же значениях t, 2 и :
а затем по формуле (6.6.3) в тех же условиях необходимый объем бесповоротной выборки:
Ответ. 1.Вероятность того, что среднее разрывное усилие проволок во всей партии отличается от среднего разрывного усилия проволок в выборке не более чем на 0,31 (по абсолютной величине) равна 0,8990. 2.С вероятностью 0,9975 можно утверждать, что среднее разрывное усилие проволок всей партии находится в границах от 44,53 до 45,67 (Н/мм2). 3.Для того, чтобы с доверительной вероятностью P=0,9961 гарантировать доверительные границы с предельной ошибкой =0,42, нужно образовать бесповторную выборку из 144 проволок.
Пример 6.6.3 По данным задачи 1 найти: 1) доверительные границы, в которых с вероятностью P=0,9545 во всей партии находится доля проволок с разрывным усилием, не меньшим 0,46; 2) каким должен быть объем выборки, чтобы с той же вероятностью 0,9545 можно было гарантировать доверительные границы с предельной ошибкой 0,05?
Решение. Находим выборочную долю
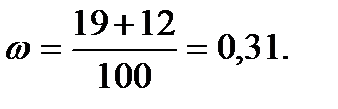
Так как оценивается генеральная доля, а выборка бесповоротная, то по формуле (1-г) подсчитаем среднюю квадратическую ошибку выборочную доли:
Теперь по таблице находим значение аргумента t из соотношения Ф(t)=0,9545. Получаем t=2. Из формулы (6.6.2) следует, что
а доверительные границы равны:
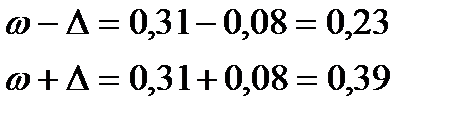
Для ответа на второй вопрос применим формулу (6.6.4-а), но сначала по формуле (6.6.4-в) находим объем повторной выборки при заданных значениях , t и , учитывая, что оценивается генеральная доля:
а затем по формуле (3-г) необходимый объем бесповоротной выборки:
Ответ. 1.С вероятностью 0,9545 можно утверждать, что во всей партии доля проволок с разрывным усилием не меньшим 46 Н/мм2 заключена в границах от 0,23 до 0,39.
2.Для того, чтобы с доверительную вероятностью P=0,9545 гарантировать доверительные границы с предельной ошибкой 0,05, нужно образовать бесповоротную выборку из 185 проволок.
Пример 6.6.4 Из числа отобранных по схеме собственно случайной бесповоротной выборки 500 зерен 20 зерен не взошли. Необходимо:
1.Определить с доверительной вероятностью 0,9545 границы процента всхожести во всей партии семян.
2.Найти доверительную вероятность, с которой можно гарантировать втрое меньшую предельную ошибку, чем найденную в п.1.
3.Найти такой объем выборки, что указанную в п.2 предельную ошибку гарантировать с вероятностью 0,99. Значение выборочной доли принять по данным предварительной выборки в 500 зерен.
Решение. Исходя из условия задачи, находим выборочную долю взошедших семян:
или 96%.
1.По величине P=0,9545 определяем по таблице приложений значение t=2.
2.Вычисляем по формуле (3-в) среднюю квадратическую ошибку выборки
Расчет производим по формулам повторной выборки, так как число семян N во всей партии можно считать значительно превосходящим объем выборки n=500 зерен.
3.Вычисляем предельную ошибку повторной выборки:
или 
Отсюда получаем доверительные границы:
и 
.
Ответ: С доверительной вероятностью P=0,9545 можно гарантировать следующие доверительные границы для процента всхожести семян во всей партии: от 94,25% до 97,75%.
II.Дано n=500, =0,96, 1= 
Определить значение P.
Решение: 1.Вычисляем среднюю квадратическую ошибку выборки (она была найдена в задаче I типа: 
).
2.Определить аргумент t по формуле (6.6.2)
3.По таблице приложений находим
Ответ. С вероятностью P=0,4971 можно гарантировать предельную ошибку выборки 
, или приблизительно 0,6%.
III.Дано P=0,99, 1=0,00583 и =0,99. Определить n.
Решение. 1.По значению P=Ф(t)=0,99 находим из таблицы t=2,577 (здесь используется интерполирование между значениями Ф(2,57)=0,9898 и Ф(2,58)=0,9901). 2.Вычисляем необходимый объем повторной выборки 
(округляем до целого числа).
Ответ. Для того, чтобы гарантировать с вероятностью P=0,99 доверительные границы для процента всхожести семян 96%0,6%, необходимо объем выборки увеличить до 7502 зерен.
