Решение дифференциальных уравнений без использования встроенных функций

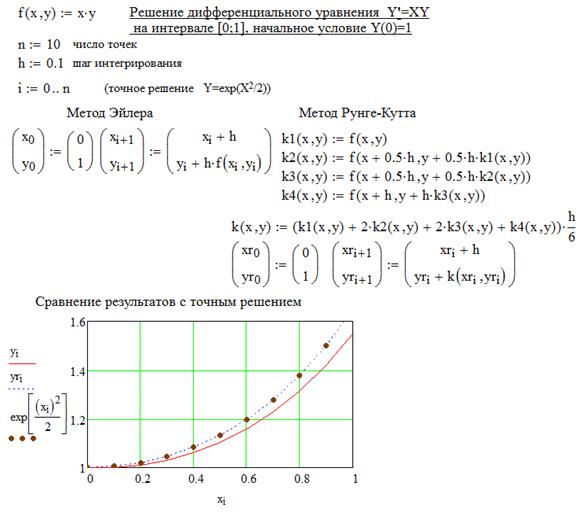
Может возникнуть вопрос: а нужно ли создавать свои документы для реализации таких методов? Ответ на него не однозначен. Если ваша цель — решение конкретной задачи, то проще воспользоваться готовыми функциями, которые будут описаны ниже. Однако реализация известных численных методов в системе MathCAD легка и наглядна. Более того, она позволяет вмешиваться в алгоритмическую реализацию методов решения, что способствует созданию новых или улучшенных методов решения дифференциальных уравнений, ориентированных на решение интересующих пользователя задач. По существу приведенные уравнения повторяют известные формулы часто встречающиеся в учебной литературе по численным методам решения дифференциальных уравнений. Кроме этого, «ручная» реализация процесса решения задачи очень полезна студентам как с точки зрения закрепления знаний по вычислительной математике, так и для более глубокого освоения системы MathCAD. На рисунке 5.1 показан пример решения дифференциального уравнения 1-го порядка методами Эйлера и Рунге-Кутта.

Рисунок 5.1 - Решение дифференциального уравнения
методами Эйлера и Рунге-Кутта

Функция rkfixed

Наиболее часто для нахождения решений дифференциальных уравнений используется встроенная функция MathCad rkfixed.

Для решения уравнения с помощью этой функции необходимо ввести в MathCad:

§ дифференциальное уравнение, записанное в виде:

y^’ = f (x, y) (5.1)

или систему n уравнений, представленную в форме:

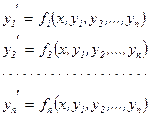(5.2)

§ начальные условия;

§ набор точек, в которых нужно найти решение.

Общий вид функции:

rkfixed (y, x1, xk, k, D),

где y - вектор начальных условий размера n, где n - число уравнений в системе. Для дифференциального уравнения первого порядка этот вектор вырождается в одну точку y₀ (эта точка должна быть записана именно как нулевой элемент вектора y');

x1, xk - граничные точки интервала, на котором ищется решение. Начальные условия, заданные в векторе y, - это значение решения в точке x1;

k - число точек (не считая начальной), в которых ищется решение. При помощи этого аргумента определяется число строк (k + 1) в матрице, возвращаемой функцией rkfixed;

D (x, y) - функция-вектор, представляющая собой вектор из n элементов, содержащих первые производные неизвестных функций (правые части системы (5.2) или уравнения (5.1)).

Функция rkfixed использует для решения метод Рунге-Кутта четвертого порядка с фиксированным шагом. В результате решения получается матрица, имеющая n +1 столбцов:

§ первый столбец содержит точки, в которых ищется решение дифференциального уравнения (значения x);

§ второй столбец содержит y₁(x), третий - y₂(x) и т.д.

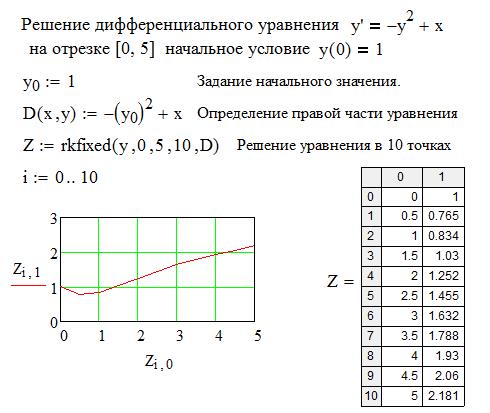
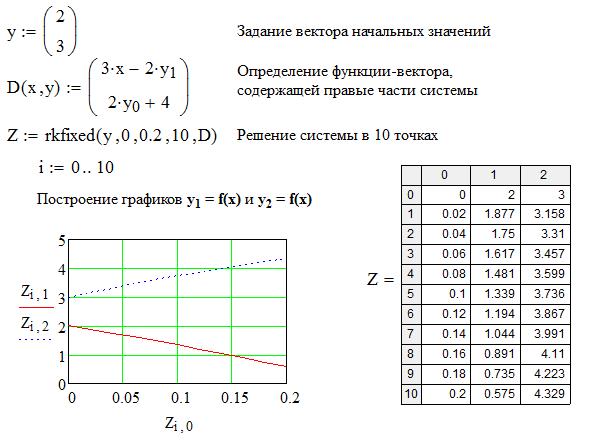
На рисунке 5.2 показаны примеры решения уравнения первого порядка, на рисунке 5.3 - системы двух уравнений.

Рисунок 5.2 - Решение дифференциального уравнения первого порядка

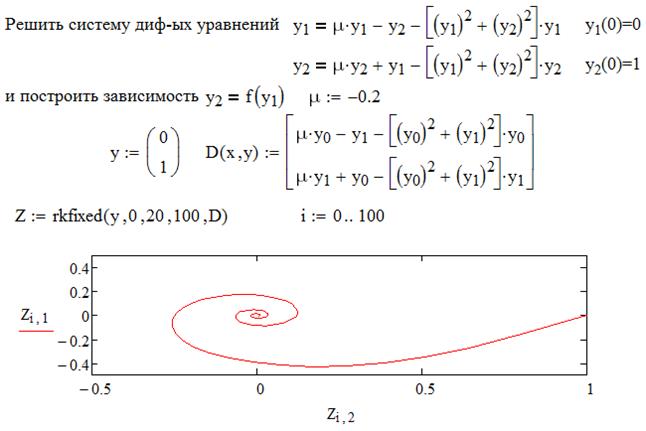
Рисунок 5.3 - Решение системы двух дифференциальных уравнений первого порядка

Для решения или систем уравнений более высоких порядков, их нужно сначала преобразовать к виду (5.2). Заметим, что любое уравнение вида

y⁽ⁿ⁾= f(x,y^(n-1),y^(n-2),…,y)

посредством замены

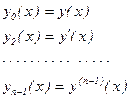
может быть сведено к виду (5.2):

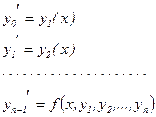
На рисунке 5.4 показан пример решения уравнения четвертого порядка, на рисунке 5.5 - системы двух дифференциальных уравнений второго порядка, сведенных к виду (5.2), по рассмотренной выше методике.

Пример 1. Решить ДУ на отрезке [ 0, 2 ]:

Показать решение на графике.

1. Введем обозначения: y → y₀, y' → y₁, y'' → y₂, y''' → y₃

2. Посредством замены, сводим ДУ к системе:

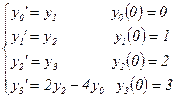
Рисунок 5.4 - Решение дифференциального уравнения четвертого порядка

Пример 2. Решить систему ДУ на отрезке [ 0, 0.4 ]:

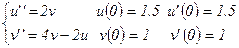Построить зависимости u(x), v(x).

1. Введем обозначения: u → y₀, u' → y₁, v → y₂, v' → y₃

2. Посредством замены, сводим данную систему ДУ к системе:

Рисунок 5.5 - Решение системы дифференциальных уравнений второго порядка

Функция odesolve

В системе MathCad 2000 появилась новая, чрезвычайно удобная функция для решения дифференциальных уравнений, которая используется совместно с ключевым словом Given и имеет вид:

odesolve(x,b,[step])

Аргументы функции:

x – переменная интегрирования;

b – конечная точка отрезка интегрирования;

step - необязательный параметр, число шагов интегрирования.

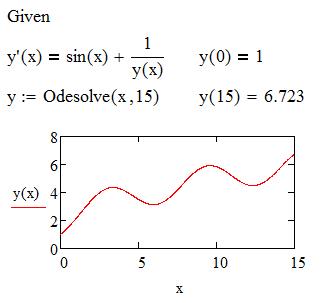
Теперь запись решения задачи Коши вполне естественна: пишется ключевое слово Given, затем дифференциальное уравнение и начальные условия. Функция odesolve, завершающая эту конструкцию, возвращает функцию – решение задачи. У этой функции нельзя просмотреть ее аналитический вид, но тем не менее это полноценная MathCad-функция пользователя, которую можно протабулировать, построить график, найти у нее особые точки – корни, минимум, максимум. На рисунке 5.6 показан пример использования данной функции для решения дифференциального уравнения первого порядка.

Рисунок 5.6 - Решение дифференциального уравнения
первого порядка с помощью odesolve

Дифференциальное выражение может быть записано с использованием операторов дифференцирования d/dx, d²/dx² или с помощью знака производной y¢(x), который вводится с помощью клавиатурной комбинации Ctrl/F7.

Условия, которые задаются в блоке решения, могут быть вида y(a)=b или y¢(a)=b, но нельзя задавать ограничения вида y¢(a)+y(a)=b.

Функция odesolve предназначена для решения уравнений, но не систем, поэтому при необходимости решить систему с помощью этой функции, ее сначала нужно преобразовать к одному уравнению по изложенной выше методике.

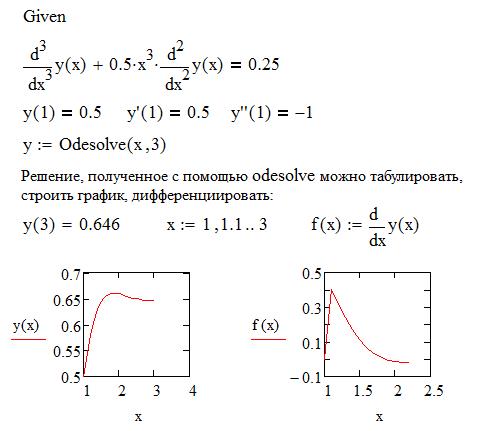
На рисунке 5.7 показан пример решения уравнения 3-го порядка с помощью функции odesolve.

Рисунок 5.7 - Решение дифференциального уравнения
третьего порядка с помощью odesolve

Функции Bulstoer, Rkadapt

Когда известно, что решение системы является гладкой функцией, то для решения дифференциальных уравнений лучше использовать функцию

Bulstoer (y, x1, xk, k, D),

куда заложен метод Булириш-Штера, а не Рунге-Кутта, используемый функцией rkfixed. В этом случае решение будет точнее.

Решение дифференциального уравнения удобнее использовать, если вычислять его достаточно часто на интервале, где искомая функция меняется быстро, и не очень часто - где функция меняется медленно. Для этого можно использовать функцию

Rkadapt (y, x1, xk, k, D).

В отличие от функции rkfixed, которая ищет решение с постоянным шагом, функция Rkadapt проверяет, как быстро изменяется приближенное решение, и, соответственно, адаптирует размер шага. Этот адаптивный контроль дает возможность данной функции вычислять решение на более мелкой сетке в тех областях, где оно меняется быстро, и на более крупной - в тех областях, где оно меняется медленно. Это позволяет повысить точность и сократить время, требуемое для решения уравнения.

Обратите внимание, что, хотя функция Rkadapt при решении использует во внутренних расчетах переменный шаг, возвращает решение она на равномерной сетке.

Список аргументов, матрица решения и порядок использования этих функции те же самые, что и для rkfixed.

Функции bulstoer, rkadapt

Функции, описанные выше, искали решение y(x) в равноотстоящих точках на отрезке [x1, xk]. Однако, иногда возникает задача, когда необходимо найти приближенное решение только в одной конечной точке интервала. Хотя функции, описанные выше, позволяют вычислить y (xk), но при этом они будут делать дополнительную работу, возвращая промежуточные значения y(x). Если необходимо вычислить только значение y (xk), лучше использовать функции, перечисленные ниже. Каждая из них соответствует одной из функций, описанной в предыдущих разделах и обладает аналогичными свойствами.

Функции имеют вид:

bulstoer (y, x1, xk, e, D, kmax, save)

rkadapt (y, x1, xk, e, D, kmax, save),

где y - вектор начальных условий;

x1, xk - граничные точки интервала, на котором ищется решение;

D - функция-вектор, описывающая исходную систему;

e - параметр, контролирующий точность решения. Малое значение e определяет меньшие шаги вдоль траектории, что увеличивает точность решения. Значение e, равное 10 ^-3 - 10 ^-5 обычно дает хороший результат;

kmax - максимальное число промежуточных точек, в которых ищется промежуточное решение. Значение kmax содержит ограничение сверху на число строк матрицы, возвращаемой этими функциями;

save - минимально допустимый интервал между точками, в которых ищется решение. Он определяет нижнюю границу различия между любыми двумя числами в первом столбце матрицы, возвращаемой функцией.

На рисунке 5.8 показан пример решения уравнения в одной точке.

Рисунок 5.8 - Решение дифференциального уравнения с помощью rkadapt