MathCad использует несколько функций для работы с распространенными законами распределения случайных величин. Эти функции распадаются на три класса:
§ плотность распределения вероятности f(x). Эта функция показывают отношение вероятности того, что случайная величина попадает в малый диапазон значений dx, к величине этого интервала;
Плотность распределения вероятности - производная от соответствующей функции распределения
f(x) = F¢ (x);
§ функция распределения F(x) определяет вероятность того, что случайная величина X будет принимать значение, меньшее фиксированного числа x, т.е.
F(x) = P(X < x)
§ обращение функций распределения позволяет по заданной вероятности p вычислить такое значение x, что P (Х < x) = p.
В таблице 6.2 приведены эти три класса функций для наиболее часто используемых законов распределения случайных величин. На рисунке 6.1 изображена связь между плотностью вероятности и функцией распределения случайной величины.

|
Рисунок 6.1 - Пример использования функций для работы
с законами распределения случайных величин
Таблица 6.2 - Функции для работы с различными
законами распределения случайных величин.
| Вид распределения | Плотность распределения | Функция распределения | Обращение функции распределения |
| Биноминальное | dbinom (k, n, p)
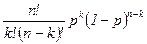
| pbinom (k, n, p) | qbinom (p, n, r)r - вероятность успеха в одиночном испытании |
| ХИ - квадрат | dchisq (x, d)

| pchisq (x, d) | qchisq (p, d) |
| Нормальное | dnorm (x, m, s)
 s > 0
s > 0
| pnorm (x, m, s) | qnorm (p, m, s) |
| Пуассона | dpois (k, l)
 l > 0 l > 0
| ppois (k,l) | qpois (p,l) |
| t - распределение Стьюдента | dt (x, d)
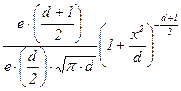 d > 0
d > 0
| pt (x, d) | qt (p, d) |
| Равномерное | dunif (x, a, b)
 
| punif (x, a, b) | qunif (p, a, b) |
Функция hist
Для вычисления частотного распределения, применяемого при построении гистограмм в MathCad существует функция
hist (int, A),
которая возвращает вектор, представляющий частоты, с которыми величины, содержащиеся в векторе А, попадает в интервалы, определяемые вектором int. Элементы в А и int должны быть вещественными. Элементы вектора int должны быть расположены в порядке возрастания. Возвращаемый результат - вектор, содержащий на один элемент меньше, чем int.
MathCad интерпретирует int как набор точек, определяющих последовательность интервалов в гистограмме. В возвращаемом функцией hist векторе f, f i - есть число значений val из A, удовлетворяющих условию:
inti ≤ val < inti+1
Данные, меньшие чем первое значение в int и большие, чем последнее значение - игнорируются. На рисунке 6.2 показан пример использования гистограммы в MathCad.

|
Рисунок 6.2 - Пример использования гистограмм в MathCad
Случайные числа
В MathCad существует набор функций для генерирования случайных чисел, имеющих разнообразные распределения вероятностей. Во всех этих функциях, представленных в таблице 6.3, первый аргумент m есть число случайных точек, содержащихся в векторе, который возвращает соответствующая функция, остальные аргументы - параметры распределения.
Таблица 6.3 - Функции для генерирования случайных чисел
| Вид распределения | Функция |
| Биноминальное | rbinom (m, n, p) |
| ХИ - квадрат | rchisq (m, d) |
| Нормальное | rnorm (m, µ, σ) |
| Пуассона | rpois (m, l) |
| Стьюдента | rt (m, d) |
| Равномерное | runif (m, a, b) rnd (x) эквивалентно runif (0, 1, x) |
Каждый раз, когда повторно вычисляется выражение, содержащее одну из этих функций, MathCad генерирует новые случайные числа. Чтобы заставить MathCad получить новые случайные числа в уже использованном выражении, нужно щелкнуть мышью на этом выражении и нажать клавишу [ F9 ].
Любая последовательность случайных чисел всегда связана с некоторым начальным значением. Каждое нажатие [ F9 ] заставляет функцию выдать новое значение из этой последовательности. Одно и то же начальное значение производит одинаковые последовательности чисел. Изменение начального значения приводит к смене последовательности случайных чисел, выдаваемых функцией.
Чтобы изменить это значение, нужно выбрать команду Математика/Параметры/Переменные и изменить начальное значение в диалоговом окне.
Чтобы перезапустить генератор случайных чисел MathCad, не изменяя стартового значения, нужно выбрать команду Математика/Параметры/Переменные и нажать “ОК”, чтобы принять текущее значение. Затем необходимо выделить щелчком мыши выражение с функцией, генерирующей случайное число и нажать [ F9 ].
Так как генератор случайных чисел был сброшен, MathCad будет производить те же самые случайные числа, которые генерировались бы после перезапуска MathCad.
Если нужно несколько раз использовать одну и ту же последовательность случайных чисел, необходимо сбрасывать генератор случайных чисел между вычислениями, как это было описано выше.
На рисунке 6.3 показан пример использования генератора случайных чисел, на рисунке 6.4 - как создать вектор случайных чисел, имеющих заданное распределение.

|
Рисунок. 6.3 - Равномерно распределенные случайные числа

|
Рисунок 6.4 - Вектор случайных чисел, распределенных по нормальному закону
СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ
Кроме численного решения задач, MathCad может производить некоторые вычисления в аналитическом виде. Выражения можно аналитически разлагать на множители, производить дифференцирование и интегрирование, разлагать функции в ряд и т.д.
Есть два основных способа выполнить символьное преобразование выражений:
§ использование символьного знака равенства;
§ выполнение преобразований с помощью меню Symbolic (Символы).
Имеется весьма существенное различие между этими двумя способами преобразований. При использовании символьного знака равенства полученные результаты вычисляются заново всякий раз при внесении любых изменений в рабочий документ, точно так же как и для численных выражений. Результат, полученный с использованием меню, автоматически модифицироваться не будет. Чтобы получить новый ответ в этом случае, нужно снова выделить исходное выражение, которое только что изменили, и снова выбрать соответствующий пункт из меню Symbolic (Символы).
Не следует ожидать очень многого от работы с аналитическими выражениями, т.к. при работе с символьными вычислениями обнаружится, что, во-первых, многие вычисления могут быть выполнены только численно, а во-вторых еще больше вычислений возвращают такие длинные ответы, что оказывается удобнее выполнять их численно (попробуйте, например, аналитически решить уравнение x 3 + a x + 1 = 0).




