Для решения одного уравнения с одним неизвестным f (z) = 0 используется функция root(f(z), z), которая возвращает значение z, при котором выражение или функция f (z) обращается в ноль.
Первый аргумент есть функция или выражение скалярного типа.
Второй аргумент - имя переменной, которая используется в выражении. Это та переменная, варьируя которой MathCad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить начальное числовое значение, которое используется как начальное приближение при поиске корня.
Задача решения уравнения в системе Mathcad разбивается на два основных этапа:
1. отделение корней и нахождение начального значения,
2. непосредственное решение уравнения с помощью функции root.
Рассмотрим на примере 1.1 выполнение этих этапов.
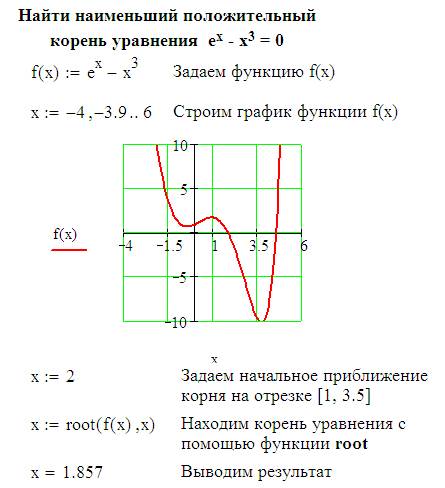
|
Рисунок 1.1 – Пример использования функции root
При использовании функции root необходимо иметь в виду следующее:
§ переменной должно быть присвоено начальное значение до начала использования функции root;
§ для выражения с несколькими корнями, начальное значение определяет корень, который будет найден MathCad. На рисунке 1.2(а) приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения;

|
Рисунок 1.2 - Использование функции root для нахождения корней уравнения
§ функция позволяет находить как вещественные, так и комплексные корни. Для поиска комплексного корня следует в качестве начального приближения взять комплексное число.
§ задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) - g(x) = 0. Для этого функция root может быть использована следующим образом: root(f(x) - g(x), x).
§ функция root предназначена только для решения одного уравнения с одним неизвестным.
MathCad при использовании функции root ищет корень методом секущих и начальное значение становится первым приближением к искомому корню. Когда значение выражения при очередной итерации становится меньше TOL, корень считается найденным, и функция root возвращает результат.
Если подходящее приближение не достигается, то появляется сообщение об ошибке, которое может быть вызвана следующими причинами:
§ уравнение не имеет корней;
§ корни уравнения расположены далеко от начального приближения;
§ выражение имеет локальные экстремумы или разрывы между начальным приближением и корнями.
Чтобы установить причину ошибки, нужно исследовать график f (x). Он поможет выяснить наличие корней уравнения f (x) = 0 и определить приблизительно их значения.
Для изменения точности нахождения корня можно изменить значение встроенной переменной TOL. При уменьшении TOL функция root будет сходиться медленнее, но ответ будет более точен.
В среде MathCad 11 появилась вторая форма функции root – с четырьмя аргументами – root(f(z),z,a,b). Первая форма (два аргумента) означает прежнее содержание этой функции – поиск корня уравнения с опорой на начальное приближение, а вторая форма (четыре аргумента) – поиск корня в заданном интервале [ a,b ]. Пример использования второй формы функции root показан на рис 1.2(б).






