Преобразования с использование меню Symbolic

Команды из меню Symbolic (Символы) обеспечивают несколько более широкое управление видами преобразований, чем использование символьного знака равенства.

Основные шаги для использования меню Symbolic (Символы) - те же самые, что и для всех команд меню:

§ заключите все, что требуется преобразовать в выделяющую рамку;

§ выберите команду из меню Symbolic (Символы);

§ MathCad поместит преобразованное выражение в рабочий документ.

Таким способом преобразовать можно не только целиком выражение, как в предыдущем случае, но и отдельные его части, заключив их в выделяющую рамку.

Ниже в этом разделе будут рассмотрены основные команды меню Символы.

Evaluate/Symbolically (Расчеты/Символические) - вычислить символьно.

Данная команда по своему действию эквивалентна символьному знаку равенства, использованному без ключевых слов.

Simplify (Упростить) - упростить выражение.

Результат этой команды - то же самое действие, которое производит символьный знак равенства совместно с ключевым словом Simplify, т.е. выполнение арифметических преобразований, сокращение общих множителей, использование основных тригонометрических тождеств, упрощение квадратных корней и степеней.

На рисунке 7.4 показаны примеры использования этого пункта меню.

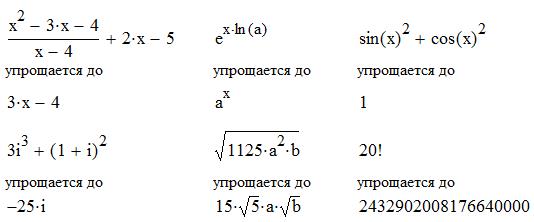
Рисунок 7.4 - Примеры использования пункта меню Simplify.

Expand (Расширить) - разложить выражение по степеням.

Данная команда аналогична по действию символьному знаку равенства, использованному совместно с ключевым словом Expand и разлагает все степени и произведения сумм в выделенном выражении. Если выражение - дробь, числитель будет разложен и выражение будет представлено как сумма дробей. Синусы, косинусы и тангенсы сумм и произведений будут разложены по мере возможности в выражения, включающие только синусы и косинусы одиночных переменных.

Так, например, cos(5 x) после разложения по степеням дает

16 cos (x)⁵- 20 cos (x)³+ 5 cos(x).

Factor (Фактор) - разложить выражение на множители.

Если выражение представляет целое число, MathCad разложит его на множители по степеням простых чисел, в остальных случаях будет сделана попытка преобразовать выражение в произведение. Так, в результате применения этого действия к числу 3546738466 будет получен ответ 2²· 3² ·7·13· 509· 709, разложение на множители выражения

(-5·x·z·y + 2·x·z² - x²·y - 2·x²·z + 3·y²·z + 6·y ·z² - 3·x·y)

дает

(x + 3·y)·(2·z + y)·(z - x).

При выборе этой команды нужно стараться выделить такую часть выражения, разложение на множители которой дает заметный результат. Так, если выделить все выражение a · b + a · c + x, то MathCad вернет это выражение неизмененным, но если выбрать только первые два члена, то будет возвращено a ·(b + c) + x.

Collect (Подобные) - приведение подобных членов.

Данная команда объединяет члены, содержащие одинаковые степени выделенного подвыражения. Выбираемое подвыражение должно быть простой переменной либо встроенной функцией вместе с аргументом. Результатом является полином от подвыражения.

Так, если выделить переменную x в любом месте выражения

x² - a·y·x² + 2·y²·x-x

и выбрать команду Collect, то в результате получим

(1 - a·y) ·x²+ (2·y² -1) ·x.

Polinomial Coefficients (Коэффициенты полинома) - коэффициенты полинома.

Многие выражения могут быть представлены в виде полиномов от выделенной переменной. Данная команда позволяет выделить коэффициенты этого полинома. Так, например, выделив переменную x в выражении

3× b× x³ - p× x + 2/3

и выполнив данную команду, получим вектор

Следующая группа команд, объединенная общим заголовком Variable (Переменные) требуетуказания (выделения) переменной, по которой выполняется соответствующее действие.

Variable/Solve (Переменные/Вычислить) – решить относительно переменной.

Чтобы решить уравнение относительно переменной, нужно:

§ напечатать уравнение или выражение. Если MathCad не находит знака равенства (введено выражение), то предполагается, что выражение требуется приравнять нулю. Не забудьте, что знак равенства вводится комбинацией “ Ctrl/= “;

§ выделить переменную, относительно которой нужно решить уравнение;

§ выбрать команду Variable/Solve.

MathCad решит уравнение относительно выделенной переменной и вставит результат в рабочий документ. Если решений получается несколько, то они представляются в виде вектора.

Можно также решить неравенство, использующее знаки >, ≥, <, ≤. Решения для неравенств отображаются в виде булевских выражений. Несколько решений также помещаются в вектор.

На рисунке 7.5 показаны примеры решения уравнений и неравенств.

Рисунок 7.5 - Примеры решения уравнений и неравенств

Variable/Substitute (Переменные/Замена) –замена переменных.

Эта команда заменяет выделенным выражением заданную переменную.

Чтобы использовать эту команду:

§ выделите выражение, которое будет заменять переменную;

§ скопируйте его в буфер обмена;

§ выделите переменную, которую нужно заменить, и выполните рассматриваемую команду.

Так, например, если в буфер обмена помещено выражение x + 3· a, а в выражении z ² + 2/ z выделена переменная z, то в результате действия команды получится: .

Variable/ Differentiate (Переменные/Дифференциалы) – дифференцировать по переменной.

Данная команда позволяет найти производную по выделенной переменной. Например, чтобы продифференцировать 2× x ² по x, нужно выделить x и выбрать из меню рассматриваемую команду, после чего MathCad отобразит результат 4× x.

Если выделить переменную y вместо x, то результат будет 1, MathCad рассматривает все переменные, кроме выделенной, как константы.

Если не выделить ни x, ни y, команда меню будет недоступна для выбора.

Variable/Integrate (Переменные/Интеграция) – интегрировать по переменной.

Ранее был рассмотрен способ аналитического вычисления неопределенных и определенных интегралов с использование знака интеграла и символьного знака равенства, как это было показано на рисунке 7.1;

Пункт меню Variable/Integrate позволяет использовать еще один способ нахождения неопределенного интеграла, при этом знак интеграла не используется, а необходимо только записать подинтегральное выражение, выделить в нем переменную, по которой нужно выполнить интегрирование, и выполнить рассматриваемую команду.

На рисунке 7.6 показан пример вычисления интегралов различными способами.

Если MathCad не может найти неопределенный интеграл, он возвращает выражение неизмененным.

При вычислении неопределенного интеграла следует помнить, что если f(x) - интеграл данной функции, то для любой константы С интегралом будет также f(x) + C.

Рисунок 7.6 - Символьное вычисление интегралов

Variable/Expand to Series (Переменные/Разложить на составляющие) -разложить в ряд

По назначению эта команда аналогична действию символьного знака равенства совместно с ключевым словом Expand, но имеются следующие отличия:

§ для задания степени разложения используется диалоговое окно, которое появляется при выборе команды;

§ команда применяется для разложения в ряд только по одной переменной;

§ разложение в ряд производится только в окрестности точки 0.

Convert to Partial Fraction (Переменные/Преобразовать в частичные доли) - разложить на элементарные дроби

Чтобы преобразовать выражение в сумму элементарных дробей, нужно выделить переменную в знаменателе выражения и выбрать команду из меню. Все константы в выражении должны быть целыми числами или дробями, но не константами с десятичной точкой.

Например, выделив переменную x в знаменателе выражения:

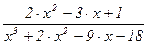
и выполнив команду, получим ответ

.

Matrix (Матрицы)- матричные операции

В эту группу команд входят три подкоманды, позволяющие выполнять символьным образом транспонирование, обращение и вычисление детерминанта матрицы.

Перед использованием этих команд необходимо заключить в выделяющую рамку всю матрицу целиком.

Примеры выполнения матричных операций приведен на рисунке 7.7

Рисунок 7.7 - Примеры выполнения матричных операций

ПРОГРАММИРОВАНИЕ

MathCad позволяет писать программы на своем собственном встроенном языке. Хотя язык программирования MathCad весьма значительно отличается от таких языков, как Бейсик, Паскаль и т.п., он содержит конструкции, во многом подобные конструкциям других языков программирования: условные операторы, операторы цикла, подпрограммы.

Написание программ в MathCad позволяет решить такие задачи, которые трудно решить другим способом.

Создание программ

Программа есть частный случай выражения MathCad. Главным отличием программы от выражения является способ задания вычислений. При использовании выражения алгоритм нахождения ответа задается одним оператором, в программе их может быть любое количество.

Алгоритмические конструкции в MathCad вводятся не традиционным набором на клавиатуре ключевых слов if, then, else, while и др., а нажатием одной из кнопок панели программирования, показанной на рисунке 8.1.

Рисунок 8.1 - Панель программирования MathCad

Щелчок по одной из этих кнопок создает на экране заготовку соответствующей программной конструкции.

Следующий пример показывает, как написать программу вычисления функции .

Конечно, эту задачу можно решить и без использования программы, но на этом примере будет показано, как создаются программы в MathCad.

§ введите левую часть определения функции и знак присваивания;
§ откройте панель программирования и нажмите на ней кнопку “Add Line”. Появится вертикальный столбец с двумя полями ввода для занесения операторов;
§ перейдите в верхнее поле, щелкнув по нему мышью или нажав клавишу “Tab”. Напечатайте Z и нажмите кнопку ““ на панели программирования;
§ в поле ввода справа от ““ введите x/y;
§ нижнее поле ввода предназначено для задания возвращаемого функцией значения log(Z);

Символ ““ в MathCad соответствует оператору присваивания, а выражение Z x/y означает, что переменной Z нужно присвоить значение, равное x/y.

Теперь рассмотренную программу можно использовать точно так же, как и любую другую функцию. На рисунке 8.2 показано два примера записи программы MathCad. Обратите внимание, что переменная Z является локальной и определена только внутри программы.

Программа может содержать любое числа операторов (второй пример рисунке 8.2). Для добавления оператора служит кнопка “ Add Line ” на панели программирования. Чтобы удалить позицию ввода, ее нужно выделить и нажать клавишу “ Del ”.

Рисунок 8.2 - Примеры простейших программ MathCad

Возвращаемым программой значением является значение последнего выражения программы. Возвращаться может число, как на рисунке 8.2, или массив чисел, как это будет показано ниже.

Условный оператор

Ниже приводится пример определения функции, задаваемой различными аналитическими выражениями на разных участках области определения:

 

§ введите левую часть определения функции и знак присваивания;
§ нажмите кнопку “Add Line” на панели программирования;
§ перейдите в верхнее поле ввода и щелкните по кнопке “ if “ на панели программирования;
§ сейчас активировано поле для ввода логического выражения. Левое поле предназначено для значения, которое будет иметь выражение, если логическое выражение справа истинно;
§ перейдите в нижнее поле ввода и нажмите кнопку “otherwise” на панели программирования;
§ введите значение, которое программа должна возвратить, если логическое выражение ложно.

На рисунке 8.3 показан график этой функции, на рисунке 8.4 - более сложная программа, использующая условный оператор, в сравнении с использованием встроенной функции if.

Рисунок 8.3 - Пример программы с использованием условного оператора

Рисунок 8.4 - Сравнение программного оператора “if” и встроенной функции “if”

8.3 Оператор цикла “while”

Структура оператора while в MathCad аналогична структуре такого же оператора Паскаля. Методика ввода операторов достаточно подробно рассмотрена в предыдущих разделах. Если программа зациклилась, то ее можно остановить нажатием клавиши “ Esc ”.

На рисунке 8.5 показан пример использования оператора “while”.

Рисунок 8.5 - Пример использования оператора “while”

8.4 Операторы “break”, “return”

Часто бывает необходимо выйти из цикла при выполнении некоторого условия. Для этого, можно использовать оператор “break”, который, так же как соответствующий оператор в Паскале, обеспечивает немедленный выход из любого оператора цикла.

Иногда требуется немедленный выход не только из цикла, но и из всей программы. Для этого служит оператор “return”, который прерывает выполнение программы-функции и возвращает значение операнда, стоящего за ним. Следующий пример поясняет работу этого оператора. Например, программа на рисунке 8.5 будет зациклена, если каждый элемент вектора v меньше, чем t. В этом случае, записанное после “while” условие никогда не станет ложным и поиск выйдет за границы вектора, что приведет к сообщению о выходе индекса за допустимые пределы.

Программа на рисунке 8.6 возвратит ноль в том случае, если все элементы вектора v меньше заданного t. В противном случае она возвращает индекс и значение первого элемента, превосходящего t.

Рисунок 8.6 - Пример использования оператора “return”

8.5 Оператор цикла “for”

Оператор цикла “for”, как и в Паскале, задает заранее определенное число повторений. Для создания цикла for:

§ щелкните по кнопке “for” на панели программирования;
§ в поле слева от знака Î введите имя переменной цикла, а в поле справа - диапазон значений, в котором должна изменяться переменная цикла. Диапазон может вводиться точно так же, как и дискретный аргумент;
§ в поле внизу введите оператор или группу операторов, представляющих тело цикла.

В верхней части рисунка 8.7 показан цикл “for”, используемый для вычисления факториала числа N.

В нижней части рисунка приведен пример, в котором переменная цикла определена не с помощью диапазона, а через элементы вектора. Необходимо отметить, что хотя выражение, справа от знака Î обычно является диапазоном, оно может быть также вектором или списком скаляров, диапазонов и векторов, разделенных запятыми.

Рисунок 8.7 - Примеры использования оператора “for”

Примеры программ

Одной из характеристик, определяющих гибкость методов программирования, является возможность использовать одни программные структуры внутри других. В MathCad это можно сделать следующими путями:

§ один из операторов можно сделать, в свою очередь, программой;

§ можно определить функцию рекурсивным методом.

В данном разделе рассмотрены три примера более сложных программ, которые трудно было бы решить без возможностей программирования.

На рисунке 8.8 показан пример программы, реализующей метод Ньютона решения нелинейного уравнения, операторы которой сами являются программой, на рисунке 8.9 - программы с вложенными циклами.

Рисунок 8.8 - Программа решения нелинейного уравнения методом Ньютона

Рисунок 8.9 - Программа нахождения простых чисел

Рекурсия является одним из мощных методов программирования и заключается в определении функции через саму себя, как это показано на рисунке 8.10.

 

Рекурсивные определения функции всегда состоят по меньшей мере из двух частей:

§ начального определения, предотвращающего бесконечную рекурсию;

§ определения функции в терминах предыдущего значения функции. Основная идея подобна идее математической функции: если можно получить значение f (n +1) из f (n) и известно f (0), то известна и вся функция f.

 

Рисунок 8.10 - Примеры рекурсивных определений функции