С помощью кубических сплайнов в MathCad можно также построить интерполяционную поверхность для экспериментальных зависимостей, редставленных в виде функции двух переменных. Для этого служат уже знакомые функции lspline, pspline, cspline и interp.
Конечно, в отличие от одномерной интерполяции, в данном случае экспериментальные значения не могут быть заданы в произвольных точках на плоскости. Интерполяционная поверхность может быть построена только в том случае, когда значения заданы в узлах прямоугольной сетки n×n. Для построения такой поверхности нужно выполнить следующую последовательность действий:
§ задать экспериментальные значения в виде квадратной матрицы Z размерности n;
§ задать матрицу M для описания сетки. Эта матрица должна состоять из двух столбцов и n строк. Каждый столбец матрицы M задает положение линий сетки по одной из координат;
§ для вычисления двумерного сплайна следует воспользоваться функцией cspline(M, Z) (также можно lspline или pspline). Результатом данной функции будет вектор, который далее нужно использовать как аргумент функции interp.
На рисунке 3.4 показан пример двумерной кубической сплайн-интерполяции.

|
Рисунок 3.4 - Пример двумерной интерполяции кубическим сплайном
Линейное предсказание
Функции интерполяции, описанные в этом разделе до сих пор, позволяют по заданным значениям некоторой функции в ряде точек оценить ее значение в промежуточных точках. Иногда бывает необходимо оценить значения функции в точках, расположенных вне области расположения сетки, на которой заданы значения функции. В MathCad есть функция predict, которая позволяет это сделать. Эта функция использует линейный алгоритм предсказания, который уверенно работает, когда экстраполируемая функция является гладкой и осциллирующей, хотя и не обязательно периодической.
Линейное предсказание можно рассматривать как разновидность экстраполяции, но оно не имеет ничего общего с линейной или полиномиальной экстраполяцией. Функция линейного предсказания имеет вид:
predict (v, m, n),
где v - вектор, содержащий значения, подлежащие обработке с целью предсказания дальнейших значений. Элементы этого вектора должны представлять собой значений, взятые для равноотстоящих узлов;
m - число последних точек в векторе v, используемых для предсказания
(m + 1)- -ой точки;
n - число предсказанных значений, возвращаемых функцией predict.
Пример использования функции predict показан на рисунке 3.5.

|
Рисунок 3.5 - Использование функции предсказания для экстраполяции данных
АППРОКСИМАЦИЯ
MathCad включает несколько функций для аппроксимации экспериментальных данных теоретической кривой, параметры которой определяются из условия минимума суммы квадратов отклонений.
В отличие от функций интерполяции, обсужденных в предыдущем разделе, эти функции не требуют, чтобы аппроксимирующая кривая или поверхность проходили в точности через точки данных, поэтому они гораздо менее чувствительны к ошибкам данных, чем функции интерполяции.
Конечный результат аппроксимации - вычисление параметров аппроксимирующей функции, с помощью которой можно, например, оценить значения в промежутках между заданными точками.
Линейная зависимость
Если известно, что зависимость между величинами x и y определяется выражением y = a x + b, то угловой коэффициент a и свободный член b могут быть найдены с помощью функций MathCad:
a: = slope (x, y);
b: = intercept (x, y),
где x - вектор значений независимой переменной;
y - вектор значений зависимой переменной.
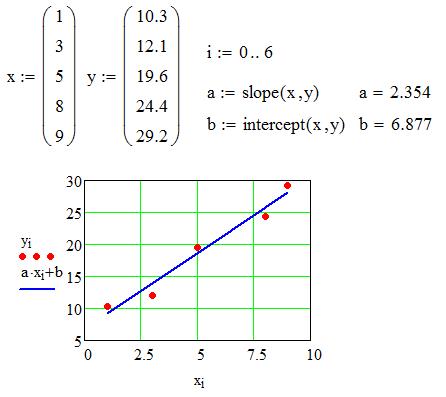
На рисунке 4.1 показан пример аппроксимации данных линейной зависимостью.
|
Рисунок 4.1 - Пример аппроксимации данных линейной зависимостью






