Любая, произвольно взятая в пространстве, плоскость может занимать общее или частное положение. Плоскостью общего положения называется плоскость, которая не перпендикулярна ни к одной из плоскостей проекций (см. рис. 5.2). Все остальные плоскости (кроме плоскостей проекций) относятся к плоскостям частного положения подразделяются на проецирующие плоскости и плоскости уровня. |Проецирующей называется плоскость, перпендикулярная к одной
из плоскостей проекций. Например, горизонтально-проецирующая плоскость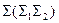 
перпендикулярна к горизонтальной плоскости проекции П1 (рис. 5.3).
Горизонтальные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с горизонтальным следом 
1. Угол 
, который образуется между плоскостями и П2, проецируется на П1 без искажения. Фронтальный след 2 перпендикулярен к оси x. Фронтально-проецирующая плоскость 
(
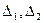) перпендикулярна к фронтальной плоскости П2 (рис. 5.4).
Фронтальные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с фронтальным следом плоскости 2. Угол 
, который образуется между заданной плоскостью и П1, проецируется на П2 без искажения. Горизонтальный след плоскости 1 перпендикулярен к оси x.
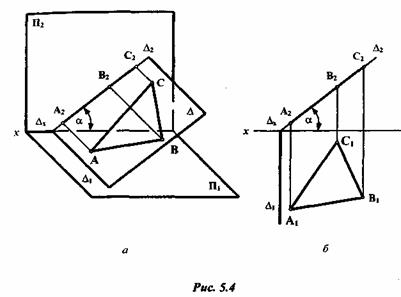
Профильно-проецирующая плоскость Т (T1, T2) перпендикулярна к профильной плоскости проекции П3 (рис. 5.5).
Профильные проекции всех геометрических образов (точек, прямых, фигур), лежащих в этой плоскости, совпадают с профильным
следом плоскости Т3. Углы и , которые образуются между заданной плоскостью и плоскостями проекций П1 П2 (
= T^П1;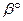 
= Т^П2), проецируются на плоскость П3 без искажений. Горизонтальный и фронтальный следы плоскости параллельны оси х.
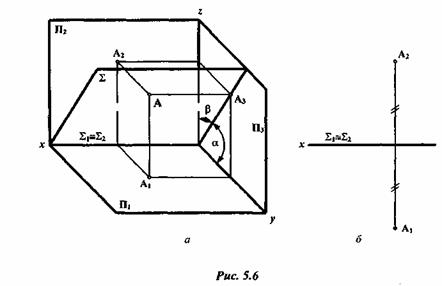
Профильно-проецирующая плоскость может проходить через ось x: (рис. 5.6).
Следы этой плоскости 1 = 2 совпадают друг с другом и с осью x, поэтому не определяют положение плоскости. Необходимо кроме следов задать в плоскости точку (рис. 5.6). В частном случае эта плоскость может быть биссекторной плоскостью. Угол ° = °, а точка А равноудалена от плоскостей проекций П1 П2.
Плоскостью уровня называется плоскость, перпендикулярная одновременно к двум плоскостям проекций и параллельная третьей. Таких плоскостей три разновидности (рис. 5.7):
· горизонтальная плоскость уровня перпендикулярна к П2, П3 и параллельна П1 (рис. 5.7, а);
· фронтальная плоскость уровня перпендикулярна к П1 П3 и параллельна П2 (рис. 5.7, б);
· профильная плоскость уровня перпендикулярна к П1 П2 и параллельна П3 (рис. 5.7 в).
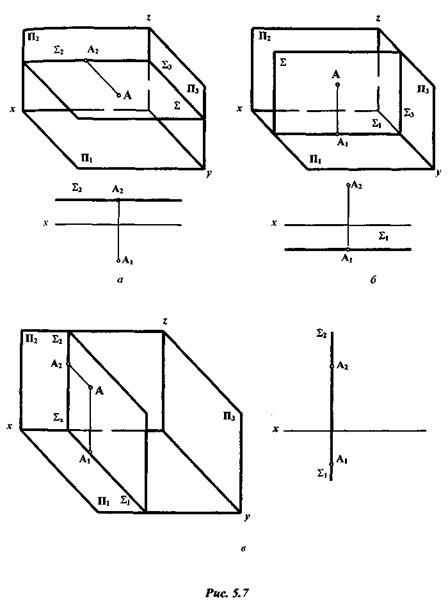
Из определения плоскостей уровня следует, что одна из проекций точки, линии, фигуры, принадлежащих этим плоскостям, будет совпадать с одноименным следом плоскости уровня, а другая проекция будет натуральной величиной этих геометрических образов.
