Основні формули
1. Диполь – це система двох однакових за модулем і протилежних за знаком зарядів, які розміщені на деякій відстані один від одного.
Електричний момент р диполя це вектор, який напрямлений від негативного заряду до позитивного і який дорівнює добутку заряду | q| на вектор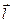 
, що проведений від негативного заряду до позитивного та називається плечем диполя, тобто
.
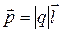Диполь має назву точкового, якщо плече l диполя значно менше відстані r від центра диполя до точки, у якій визначається дія диполя (l << r).
2. Напруженість поля точкового диполя визначається за формулою
,
де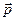 
– електричний момент диполя;
r – абсолютне значення радіуса вектора, який проведений від центра диполя до точки, напруженість поля в якій визначається;
– кут між радіусом-вектором r та плечем l диполя.
Напруженість поля точкового диполя у точці, яка лежить на осі диполя ( = 0)
,
і в точці, яка лежить на перпендикулярі до плеча диполя, що проведений із його середини (а = 
/2)
.
3. Потенціал поля точкового диполя на відстані r від диполя
.
4. Потенціал поля точкового диполя у точці, яка лежить на осі диполя ( = 0)
,
і в точці, яка лежить на перпендикулярі до плеча диполя, який проведений із його середини ( = / 2)
.
Напруженість і потенціал неточкового диполя визначаються як для системи зарядів.
Механічний момент, який діє на диполь з електричним моментом 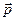, розміщеним в однорідному електричному полі з напруженістю Е
або 
,
де а – кут між напрямками векторів 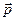та 
.
У неоднорідному електричному полі, окрім механічного моменту (пари сил), на диполь діє ще деяка сила. У випадку поля, яке має симетрію відносно осі х, ця сила виражається співвідношенням
,
де 
– частинна похідна напруженості поля, яка характеризує ступінь неоднорідності поля у напрямку осі х.
При а > 
сила Fх позитивна. Це означає, що під її дією диполь втягується в область сильного поля.
5. Електричне зміщення D пов'язане з напруженістю Е електричного поля таким співвідношенням
.
Це співвідношення може бути застосованим лише для ізотропних діелектриків.
6. Потік вектора електричного зміщення визначається аналогічно потоку вектора напруженості електричного поля:
– у випадку однорідного поля
;
– у випадку неоднорідного поля
,
де Dn – проекція вектора 
на напрямок нормалі до елемента поверхні, площа якої дорівнює dS.
7. Теорема Гаусса для поля в діелектриках. Потік вектора електричного зміщення через будь-яку замкнену поверхню дорівнює алгебраїчній сумі сторонніх зарядів, які охоплені цією поверхнею:
,
де п – кількість сторонніх зарядів, які охоплені замкнутою поверхнею.
