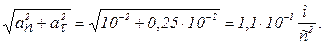С. Г. Авдєєв, Т. І. Бабюк
О. С. Камінський
ЗБІРНИК ЗАДАЧ З ФІЗИКИ
Частина 1
(механіка, електрика, електромагнетизм)
Міністерство освіти і науки України
Вінницький національний технічний університет
С. Г. Авдєєв, Т. І. Бабюк
О. С. Камінський
ЗБІРНИК ЗАДАЧ З ФІЗИКИ
Частина 1
(механіка, електрика, електромагнетизм)
Вінниця
ВНТУ
УДК 530(078)
ББК 22.3я77
А18
Рекомендовано до друку Вченою радою Вінницького національного технічного університету Міністерства освіти і науки України (протокол № 5 від 24.12.09 р.)
Рецензенти:
І. О. Сівак, доктор технічних наук, професор
О. В. Осадчук, доктор технічних наук, професор
В. Г. Дзісь, кандидат фізико-математичних наук, доцент
Авдєєв, С. Г.
А18Збірник задач з фізики. Ч.1 (механіка, електрика, електромагнетизм): навчальний посібник / С. Г. Авдєєв, Т. І. Бабюк, О. С. Камінський. – Вінниця: ВНТУ, 2010. – 123 с.
Збірник задач складається з розділів “Механіка, електрика і електромагнетизм”, які традиційно викладаються в одному триместрі. Кожен окремий розділ супроводжується короткими теоретичними викладками і прикладами розв’язування задач.
В першу чергу збірник задач призначений для організації та проведення практичних занять з курсу загальної фізики студентами вищих технічних навчальних закладів. Велика кількість і різноманітність задач, які ввійшли до збірника задач, дозволяє широко організовувати самостійну та індивідуальну роботу студентів.
УДК 53(078)
ББК 22.3я77
© С. Авдєєв, Т. Бабюк, О. Камінський, 2010
ЗМІСТ
Частина 1
Кінематика. Основні формули............................................................................................ 4
Приклади розв’язування задач............................................................................................. 7
Динаміка прямолінійного руху. Основні формули....................................................... 9
Закони збереження. Робота й енергія. Основні формули........................................... 10
Приклади розв’язування задач.......................................................................................... 11
Динаміка твердого тіла. Основні формули................................................................... 14
Приклади розв’язування задач.......................................................................................... 18
Гідростатика. Основні формули...................................................................................... 25
Задачі...................................................................................................................................... 27
Електричне поле у вакуумі. Основні формули............................................................. 46
Електричне поле у діелектриках. Основні формули.................................................... 51
Провідники в електричному полі. Основні формули.................................................. 53
Енергія електричного поля. Основні формули............................................................. 55
Приклади розв’язування задач........................................................................................... 56
Електричний струм. Основні формули........................................................................... 67
Приклади розв’язування задач........................................................................................... 71
Задачі................................................................................................................................. 75
Магнетне поле у вакуумі і середовищі. Основні формули......................................... 89
Приклади розв’язування задач........................................................................................... 95
Електромагнетна індукція. Основні формули............................................................. 100
Приклади розв’язування задач........................................................................................ 102
Рух заряджених частинок в електромагнетному полі. Основні формули............ 105
Задачі.................................................................................................................................... 105
Література........................................................................................................................... 116
Додаток А........................................................................................................................... 117
Частина 1
Кінематика
Основні формули
1. Положення матеріальної точки у просторі задається радіусом-вектором 
:
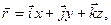
де 
, 
, 
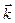– орти (одиничні вектори в напрямі координатних осей x,y,z);
x, y, z – координати точки.
Кінематичні рівняння руху в координатній формі мають вигляд
, 
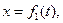
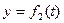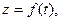
де t – час.
2. Середня швидкість
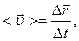
де ∆ –переміщення матеріальної точки за інтервал часу ∆ t.
Середня швидкість на шляху ∆s:
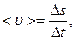
де ∆s – шлях, що пройшла точка за інтервал часу ∆ t. Миттєва швидкість
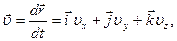
де 
– проекції швидкості υ на осі координат.
Абсолютне значення швидкості
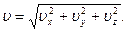
3. Прискорення
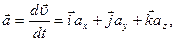
де ax, ay, az – проекції прискорення a на осі координат або
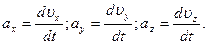
Абсолютне значення прискорення
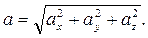
При криволінійному русі прискорення можна подати як суму нормальної і тангенціальної складових
,
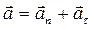де an і aτ – відповідно нормальне і тангенціальне прискорення. Вони дорівнюють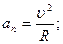 
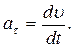
Тоді можна записати, що
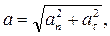
де R – радіус кривини у даній точці траєкторії.
4. Кінематичне рівняння рівномірного руху матеріальної точки вздовж осі x
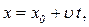
де x0 – початкова координата.
При рівномірному русі υ= const, a = 0.
5. Кінематичне рівняння рівнозмінного руху (a = const) вздовж осі x
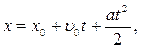
де υ0 – початкова швидкість.
Швидкість точки при рівнозмінному русі
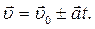
6. При обертанні положення твердого тіла визначається кутом повороту радіуса-вектора . Кінематичне рівняння обертального руху має вигляд
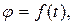
де φ – кут повороту (або кутове переміщення).
7. Середня кутова швидкість
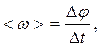
де Δφ –зміна кута повороту за час Δ t.
Миттєва кутова швидкість
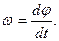
8. Кутове прискорення
9. Кінематичне рівняння рівномірного обертання
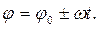
При рівномірному обертанні ω= const,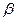 
= 0. Частота обертання
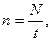або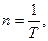 
де N – число обертів, що здійснюється за час t;
Т – період обертання (час одного повного оберту).
10. Кінематичне рівняння рівнозмінного обертання ( 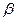= const)
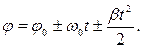
Кутова швидкість тіла при рівнозмінному русі
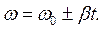
11. Зв’язок між лінійними та кутовими величинами, що характеризують обертання матеріальної точки, задається такими співвідношеннями:
а) довжина дуги кола радіусом R визначається формулою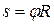 
(
– центральний кут);
б) лінійна швидкість точки
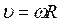або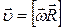 
.
Прискорення точки:
а) тангенціальне
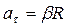або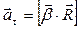 
;
б) нормальне
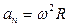або 
.
Приклади розв’язання задач
Приклад 1. Рівняння руху матеріальної точки вздовж осі х має вигляд х = A + Bt + Ct3, де A = 2 м; В = 1 м/с; С = - 0,5 м/с3. Знайти координату швидкість і прискорення точки в момент часу 2с.
Дано:
x = A + Bt + Ct3
A = 2 м
В = 1 м/с
С = - 0,5 м/с3
t = 2 c
__________
x –?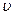 
–? a –?
Розв’язання. Координату точки знайдемо, підставивши в рівняння руху числові значення коефіцієнтів А, В, С і часу t:
x = (2+1×2 - 0,5×23) м = 0.
Оскільки потрібно знайти швидкість і прискорення в певний момент часу (t = 2 c), то це означає, що потрібно визначити миттєві величини 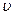x і ах.
Миттєва швидкість є першою похідною від координати за часом
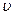x =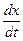 
= B + 3Ct2 .
Прискорення точки знайдемо, взявши першу похідну від швидкості за часом,
ax =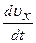 
= 6Ct.
Виконавши необхідні обчислення для моменту часу t = 2 c, одержимо
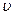x = (1 - 3 × 0,5 × 22) м/с = - 5 м/с,
аx = 6 (- 0,5) × 2 м/с2 = - 6 м/с2.
Приклад 2. Диск радіусом 0,1 м, що перебував у стані спокою, почав обертатися з постійним кутовим прискорення 0,5рад/с2. Знайти тангенціальне, нормальне й повне прискорення точок на ободі диска через дві секунди після початку обертання.
Дано:
R = 0,1 м
w(0) = 0
b = 0,5 рад/с2
t = 2с
_________ ______
аt –? an –? a –?
Розв’язання. Тангенціальні й нормальні прискорення точок тіла, яке здійснює обертальний рух, виражаються формулами
at = 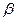R, (1)
an = w2R, (2)
де 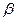– кутова прискорення тіла;
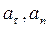– відповідні прискорення точок на ободі диска;
R – радіус диска.
В умові задачі задане кутове прискорення, яке визначається формулою
b =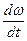 
. (3)
Отже, кутова швидкість точок через час t дорівнює
w = w(0) + b t, (4)
причому за умовою задачі початкова кутова швидкість w(0) = 0.
Виходячи із співвідношень (2) і (4), одержуємо формулу для нормального прискорення
an = w2 R = b2 t2 R.
У момент часу t = 2 с нормальне прискорення дорівнює
an = b2 t2 R = 0,52×22×0,12 = 0,1 м/с2,
тангенціальне прискорення
аt = bR = 0,5×0,1 = 0,05 м/с2,
повне прискорення
а = 
