»ндекс рентабельности (–≤) показывает, сколько единиц современной величины денежного потока приходитс€ на единицу предполагаемых первоначальных затрат, т. е.
 . [8.20]
. [8.20]
≈сли –≤ > 1, то современна€ стоимость денежного потока превышает первоначальные инвестиции, обеспечива€ тем самым наличие положительной величины NPV. ѕри этом норма рентабельности превышает заданную, и проект следует прин€ть.
≈сли –≤ = 1, то величина NPV = 0, и инвестиции не принос€т дохода.
≈сли –≤ < 1, то проект не обеспечивает заданного уровн€ рентабельности, и его следует отклонить.
ќбщим во всех случа€х прин€ти€ решени€ по реализации проекта €вл€етс€ уравнение –≤ > 1.
—ледует объ€снить, что этот метод €вл€етс€ продолжением первого, а следовательно, индекс рентабельности можно рассчитать как отношение:
 .
.
“аким образом, проект по внедрению нового оборудовани€ следует при-н€ть, так как при этом норма рентабельности превышает заданную (–≤ > 1).
ѕроект, по которому обеспечиваетс€ наибольша€ рентабельность инвестиций, €вл€етс€ предпочтительным из всех возможных.
ћетод оценки эффективности проектов с использованием внутренней нормы доходности (IRR). Ёто наиболее широко используемый критерий эффективности инвестиций.
¬нутренн€€ норма доходности Ц это процентна€ ставка, при которой чиста€ современна€ стоимость инвестиционного проекта равна нулю.
–асчЄт внутренней нормы доходности проводитс€ по формуле:
IRR = r, при котором NPV = f (r) = 0,
(внутренн€€ норма доходности (IRR) соответствует дисконту (r), при котором чиста€ современна€ стоимость инвестиционного проекта (NPV), представл€юща€ собой функцию от дисконта ( ), равна нулю).
), равна нулю).
“о есть внутренн€€ норма доходности определ€етс€ решением уравнени€:
 . [8.21]
. [8.21]
Ќетрудно заметить, что при NPV = 0 современна€ стоимость проекта (PV) равна по абсолютной величине первоначальным инвестици€м (I«) и, следовательно, они окупаютс€. ¬ общем случае чем выше величина IRR, тем больше эффективность инвестиций. ¬ практике инвестиционного анализа величина IRR сравниваетс€ с заданной нормой дисконта r. ѕри этом, если IRR > r, то проект обеспечивает положительную NPV и доходность, равную IRR Ц r.
≈сли IRR < r, затраты на проект превышают доходы, и проект €вл€етс€ убыточным. ќбщим правилом выбора проекта дл€ реализации €вл€етс€ превышение внутренней нормы доходности (IRR) над заданной нормой дисконта (r), т. е. IRR > r.
¬ финансовых расчЄтах при анализе эффективности планируемых инвестиций IRR показывает максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом. примеру, если проект полностью финансируетс€ за счЄт ссуды коммерческого банка, то значение IRR показывает верхнюю границу допустимого уровн€ банковской процентной ставки, превышение которой делает проект убыточным.
–ешение этого уравнени€ относительно IRR проводитс€ итерационным методом с использованием табулированных значений дисконтирующих множителей. ƒл€ этого с помощью таблиц выбирают два значени€ коэффициента дисконтировани€ (r1 > r2) таким образом, чтобы в интервалах r1 и r2 функци€ NPV = f (r) мен€ла своЄ значение с Ђ+ї на ЂЦї или с ЂЦї на Ђ+ї. ƒалее примен€ют формулу:
|
|
|
 , [8.22]
, [8.22]
где r1 Ц значение табулированного коэффициента дисконтировани€, при котором f (r1) > 0 (f (r1) < 0);
r2 Ц значение табулированного коэффициента дисконтировани€, при котором f (r2) < 0 (f (r2) > 0).
Ќаилучша€ аппроксимаци€ вычислений с использованием табулированных значений достигаетс€ в случае, когда длина интервала (r1, r2) минимальна (равна 1 %), т. е. в этом случае r1 и r2 €вл€ютс€ ближайшими друг к другу значени€ми коэффициента дисконтировани€, удовлетвор€ющими услови€м (в случае изменени€ знака с Ђ+ї на ЂЦї функции NPV = f (r)). ¬ этом случае значение r1Ц значение табулированного коэффициента дисконтировани€, минимизирующее положительное значение показател€ NPV, т.е.
 ;
;
r2 Ц значение табулированного коэффициента дисконтировани€, максимизирующее отрицательное значение показател€ NPV, т.е.
 .
.
¬заимной заменой коэффициентов дисконтировани€ r1 и r2 аналогичное условие можно сформулировать дл€ ситуации, когда функци€ мен€ет знак с ЂЦї на Ђ+ї.
примеру, предпри€тие рассматривает возможность реализации инвестиционного проекта, генерирующего следующий денежный поток в размере 200 тыс. грн., 400 тыс. грн., 700 тыс. грн. на прот€жении 3 лет его реализации. Ќачальна€ сумма инвестиции 900 тыс. грн. “ребуетс€ определить значение показател€ IRR дл€ проекта.
ѕоследовательность рассуждений дл€ решени€ задачи следующа€:
выбираетс€ два произвольных значени€ коэффициента дисконтирова-ни€, к примеру, r1 = 10 % и r2 = 20 %;
рассчитаетс€ NPV дл€ генерируемых денежных потоков (см. табл. 31).
ѕутЄм нескольких итераций мы определим ближайшие целые значени€ коэффициента дисконтировани€, при которых NPV мен€ет знак: это при r = 17 % NPV = + 0,20; при r = 18 % NPV = Ц 17,1. “огда уточнЄнное значение IRR будет равно
 .
.
“аким образом, истинное значение IRR = 17,01 %.
“аблица 31 –асчЄт NPV дл€ генерируемого потока
| √од | ѕоток

|  Ц дл€ r = 10 % Ц
табулированы Ц дл€ r = 10 % Ц
табулированы
| 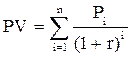 ;
(гр.2 x гр.3) ;
(гр.2 x гр.3)
| ||
| Ц900 | 1,000 | Ц900,0 | |||
 1 1
| +200 | 0,909 | +181,8 | ||
| +400 | 0,826 | +330,4 | |||
| +700 | 0,751 | +525,7 | |||
 (»того)
(»того)
| Ц | Ц | +137,9 | ||
| Ц900 | 1,00 | Ц900,0 | ||
| +200 | 0,833 | +166,6 | |||
 2 2
| +400 | 0,694 | +277,6 | ||
| +700 | 0,579 | +405,3 | |||
| NPV | Ц | Ц | Ц50,5 | ||
| Ц900 | 1,00 | Ц900,0 | |||
 1 1
| +200 | 0,862 | +172,4 | ||
| +400 | 0,743 | +297,2 | ||
| +700 | 0,641 | +448,7 | |||
| NPV | Ц | Ц | +18,3 | ||
| Ц900 | 1,00 | Ц900,0 | |||
| +200 | 0,855 | +171,0 | ||
 2 2
| +400 | 0,731 | +292,4 | ||
| +700 | 0,624 | +436,8 | |||
| NPV | Ц | Ц | +0,20 | ||
| Ц900 | 1,00 | Ц900,0 | |||
 1 1
| +200 | 0,847 | +169,4 | ||
 2 2
| +400 | 0,718 | +287,2 | ||
| +700 | 0,609 | +426,3 | |||
| NPV | Ц | Ц | Ц17,1 | ||
| Ц900 | 1,00 | Ц900,0 | |||
| +200 | 0,840 | +168,0 | ||
| +400 | 0,706 | +282,4 | |||
| +700 | 0,593 | +415,1 | |||
| NPV | Ц | Ц | Ц34,5 |
ќпределение срока окупаемости инвестиций как метод оценки их эффективности. “акой метод не предполагает временной упор€доченности денежных поступлений и €вл€етс€ самым простым и наиболее используемым в практике инвестиционного анализа. јлгоритм расчЄта срока окупаемости (––) зависит от равномерности распределени€ прогнозируемых доходов от инвестиции. ≈сли доход распределЄн по годам равномерно, то срок окупаемости рассчитываетс€ делением единовременных затрат на величину годового дохода, обусловленного ими. ѕри получении дробного числа оно округл€етс€ до ближайшего целого в сторону увеличени€. ≈сли прибыль распределена неравномерно, то срок окупаемости рассчитываетс€ пр€мым подсчЄтом числа лет, в течение которых инвестици€ будет погашена кумул€тивным доходом. ‘ормула дл€ расчета срока окупаемости проекта в общем виде имеет вид:
|
|
|
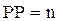 , при котором
, при котором 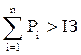 ,
,
(срок окупаемости проекта равен количеству лет (n), на прот€жении которых сумма денежных потоков (–≥) будет выше начальной инвестиции (I«)).
–асчЄт коэффициента эффективности инвестиции как метод оценки эффективности инвестиционного проекта. ’арактерными чертами такого метода €вл€ютс€:
во-первых, то, что он не предполагает дисконтировани€ показателей дохода;
во-вторых, доход характеризуетс€ показателем чистой прибыли (PN) (балансова€ прибыль за минусом отчислений в бюджет).
Ўирокое использование метода определ€етс€ простотой алгоритма расчета показател€. ќн рассчитываетс€ делением среднегодовой прибыли (PN) на среднюю величину инвестиции и умножаетс€ на 100 (коэффициент берЄтс€ в процентах). —редн€€ величина инвестиции находитс€ делением исходной суммы капитальных вложений на два, если предполагаетс€, что по истечении срока реализации анализируемого проекта все капитальные затраты будут списаны. ≈сли допускаетс€ наличие остаточной или ликвидационной стоимости (RV), то еЄ оценка должна быть исключена.
оэффициент эффективности инвестиции (ARR) рассчитываетс€ по формуле:
 .
.
ƒанный показатель сравниваетс€ с коэффициентом рентабельности авансированного капитала, рассчитываемого делением общей суммы чистой прибыли предпри€ти€ на общую сумму средств, авансированных в его де€тельность (итог среднего баланса).
Ќедостатком метода €вл€етс€ полное отсутствие учЄта временной составл€ющей денежных потоков.
јнализ ценных бумаг
јкци€ Ц это ценна€ бумага, свидетельствующа€ о внесении средств на развитие акционерного общества или предпри€ти€ и дающа€ право еЄ владельцу на получение части прибыли акционерного обще≠ства (предпри€ти€) в виде дивидендов. јкции выпускаютс€ без уста≠новленного срока их обращени€ и бывают именные и на предъ€вител€. ‘изические лица могут быть владельцами только именной акции. “ака€ акци€, переданна€ другому лицу, тер€ет свою силу (дивиденды на неЄ не начисл€ютс€, и обратно она не принимаетс€). »менна€ ценна€ бу≠мага может быть передана другому владельцу путЄм нотариального оформлени€ или через брокерские конторы, банки, имеющие лицензию на операции с ценными бумагами.
–азличают акции трудового коллектива, предпри€ти€, акционер≠ного общества. јкции трудового коллектива распростран€ютс€ только среди работников данного предпри€ти€; акции предпри€ти€ Ц среди других юридических лиц; акци€ акционерного общества Ц это эмисси≠онна€ ценна€ бумага, закрепл€юща€ право еЄ владельца (акционера) на получение части прибыли в виде дивидендов, на участие в управлении акционерным обществом и на часть имущества, остающегос€ после его ликвидации.
јкции акционерного общества бывают двух категорий: обыкно≠венные и привилегированные. —умма привилегированной акции не должна превысить установленную законодательством долю от устав≠ного капитала общества (в процентах).
ќбыкновенна€ акци€ даЄт право на участие в управлении акцио≠нерным обществом (одна акци€ Ц один голос) и участвуют в распреде≠лении чистой прибыли общества после пополнени€ резервов и выплаты дивидендов по привилегированным акци€м.
ѕривилегированные акции не дают право не участие в управле≠нии, но принос€т посто€нный (фиксированный) дивиденд и имеют преимущество перед обыкновенными акци€ми при распределении при≠были и ликвидации общества.
|
|
|
јкционеру на все принадлежащие ему акции выдел€етс€ сертифи≠кат. —ертификат акции Ц это ценна€ бумага, котора€ €вл€етс€ свиде≠тельством владени€ поименованного в нЄм лица определенным числом акций. јкционеру бесплатно выдел€етс€ один сертификат на все при≠надлежащие ему акции в случае их полной оплаты. ƒополнительные сертификаты выдаютс€ за дополнительную плату. ”тер€нный сертифи≠кат возобновл€етс€ за плату. ѕередача сертификата от одного лица к другому означает совершение сделки и переход права собственности на акции только в случае регистрации операции в установленном пор€дке.
јкци€ имеет номинальную и рыночную стоимость. ÷ена акции, обозначенна€ на ней, €вл€етс€ номинальной стоимостью акции. ÷ена, по которой реально покупаетс€ акци€, называетс€ рыночной ценой, или курсовой стоимостью (курс акции). урс акций находитс€ в пр€мой зависимости от размера получаемого по ним дивиденда и в обратной зависимости от уровн€ банковского процента за кредит.
 .
.
примеру, дивиденд по акци€м Ц 60 %, банковский процент по вкладам Ц 30 %, номинальна€ стоимость акции 1 грн. “огда:
 .
.
–ыночна€ стоимость акции рассчитываетс€ по формуле:
 .
.
ѕо данному примеру значение показател€ составит:
 .
.
ѕроцесс установлени€ цены акции в зависимости от реально при≠носимого ею дохода называетс€ капитализацией дохода и осуществл€≠етс€ через фондовые биржи, рынок ценных бумаг.
урсова€ цена акции закрытого акционерного общества, по кото≠рой она продаЄтс€ внутри общества, определ€етс€ стоимостью чистых активов общества, приход€щихс€ на одну оплаченную акцию, и назы≠ваетс€ балансовой стоимостью акций:
 ,
,
где ¬ Ц балансова€ стоимость акции, грн;
„ Ц чистые активы акционерного общества, грн;
ј Ц количество оплаченных акций, ед.
„истые активы представл€ют собой его активы за вычетом долгов (расчЄты с кредиторами, заЄмные средства, доходы будущих периодов и др.). ƒл€ кредитной организации чистые активы соответствуют пон€≠тию собственные средства (капитал). Ѕалансова€ стоимость акции примен€етс€ и при листинге акций. ¬ отдельных случа€х (дл€ финан≠сового и инвестиционного анализа, дл€ расчЄта цены акции при про≠даже еЄ внутри общества) стоимость акции можно рассчитать исход€ из величины чистой прибыли: 
 ,
,
где р Ц расчЄтна€ курсова€ стоимость акции, грн.;
ѕ Ц сумма чистой прибыли общества за последние12 мес€цев, грн.;
ј Ц количество оплаченных акций, ед.;
— Ц средн€€ ставка Ќационального банка ”краины за 12 мес€≠цев по централизованным кредитам, %.
примеру, чиста€ прибыль акционерного общества закрытого типа за год Ц 200 000 грн. оличество оплаченных акций Ц 5 тыс. шт. —редн€€ ставка Ќационального банка ”краины по централизованным кредитам Ц 25 % годовых. “огда расчЄтна€ курсова€ стоимость акции ( р) составит:
 грн.
грн.
–азница между курсами ценных бумаг, ценой продавца и ценой покупател€ носит название Ђмаржаї.
торгам на фондовой бирже допускаютс€ только проверенные ак≠ции. ѕроверка качества ценных бумаг и допуск их к биржевым торгам производитс€ с помощью процедуры листинга. Ћистинг Ц это допуск ценных бумаг эмитента к торгам на фондовой бирже путЄм включени€ их в котировочный лист и контроль финансово-хоз€йственной де€≠тельности и положени€ эмитента на предмет его соответстви€ требова≠ни€м, предъ€вленным фондовой биржей.
ќн состоит из процедуры включени€ ценных бумаг эмитентов в листинг организации торгов ценными бумагами, проведени€ их коти≠ровки, контрол€ за состо€нием листинговых ценных бумаг. ¬ключение ценных бумаг эмитента в листинг даЄт преимущество как эмитентам, так и инвесторам.
|
|
|
Ёмитентам листинг позвол€ет:
подн€ть их престиж вследствие того, что им удалось доказать устойчивое финансовое состо€ние и пройти процедуру листинга;
осуществл€ть дополнительную рекламу через биржевые каналы, а также в ведущих экономических издани€х, публикующих ко≠тировку ценных бумаг, включенных в листинг;
успешно размещать последующие выпуски ценных бумаг.
ѕреимущества инвестора заключаетс€ в следующем:
прохождение процедуры листинга даЄт гарантию надЄжности ценных бумаг;
организаци€ торгов листинговыми ценными бумагами на бирже позвол€ет определить их объективную рыночную стоимость.
ачество акции как любой другой ценной бумаги, характеризуетс€ еЄ ликвидностью. Ћиквидность ценной бумаги представл€ет еЄ способ≠ность быстро и без потерь в цене превращатьс€ в наличные деньги. ÷енные бумаги Ц это легко реализуемые активы. ”ровень ликвидности ценных бумаг определ€етс€ в процессе анализа финансового состо€ни€ эмитента. ќперативную оценку ликвидности ценной бумаги можно произвести по коэффициенту немедленной ликвидности:
 ,
,
где л Ц коэффициент немедленной ликвидности ценных бумаг;
Ѕ Ц ценные бумаги, грн.;
« Ц обща€ сумма задолженности предпри€ти€ (краткосрочные ссуды, срок оплаты которых наступил, и кредиторска€ за≠долженность) грн.
„ем выше данный коэффициент, тем выше ликвидность, т.е. воз≠можность погасить долги.
ачество ценных бумаг характеризуетс€ также адекватностью покрыти€ процентов по облигаци€м и дивидендов по акци€м чистой прибылью акционерного общества.
ѕри анализе спроса и предложени€ на акции можно использовать также такие показатели, как абсолютна€ величина спрэда, его уровень в процентах к максимальной цене спроса, соотношение объЄмов, средне≠взвешенные цены спроса и предложени€ на акции.
—прэд Ц это разрыв между минимальной ценой предложени€ и максимальной ценой спроса.
примеру, минимальна€ цена предложени€ на акцию 20,5 грн., максимальна€ цена спроса 19,5 грн. тогда величина спрэда составит (20,5 Ц 19,5) = 1,0 грн., а его уровень в процентах к максимальной цене спроса составит (1,0 / 19,5) Ј 100 = = 5,1282 %. Ќаиболее ликвидными €вл€ютс€ ценные бумаги, у которых отношение спрэда к максимальной цене спроса наименьшее (например от 0 до 3 %).
ѕри анализе спроса и предложени€ на акцию можно использовать также показатель рендит. –ендит Ц это относительный показатель до≠ходности ценной бумаги. –ендит акции рассчитываетс€ как процентное отношение выплаченного дивиденда к рыночному курсу акции. „ем выше размер рендита, тем доходнее акци€.
примеру, акци€ номиналом 1 грн. продаЄтс€ за 50 грн. ƒивиденды по ней составили в прошлом году 250 % годовых, или 250Ј1 = 2,5 грн. –ендит акции равен (2,5 / 50) x 100 = 5%.
ѕокупка акций всегда св€зана с риском. ѕри покупке акций инве≠стору целесообразно рассчитать еЄ реальную стоимость. –еальна€ стоимость акции может рассматриватьс€ как стоимость будущих де≠нежных поступлений по ней. Ёти ожидаемые денежные поступлени€ состо€т из двух элементов: из суммы ежегодно ожидаемых дивидендов и из цены, за которую инвестор предполагает продать эту акцию в бу≠дущем.
“аким образом, цена продажи акции сегодн€ зависит от размера дивидендов и цены продажи акции, котора€ будет завтра.
÷ена продажи акции рассчитываетс€ по формуле:
 ,
,
где –0 Ц рыночна€ цена акции в текущем году, т.е. сразу же после получени€ по ней дивидендов, грн;
ƒ Ц дивиденды, которые инвестор рассчитывает получить по акции в ≥-ом году, грн.;
n Ц общее число лет;
≥ Ц текущий номер года;
r Ц минимально необходима€, по мнению инвестора, нома при≠были, которую он может получить по другим инвести≠ци€м (дисконт, в дол€х единицы);
–1 Ц рыночна€ цена акции в следующем году после текущего, грн.
примеру, акци€ имеет номинальную стоимость 1 грн. ÷ена еЄ продажи Ц 5 грн. »нвестор предполагает, что рыночна€ цена акции в следующем году после текущего года может составить 8 грн. ƒиви≠денды по ней будут несколько выше дивидендов текущего года, а именно 250 % годовых, что при номинале в 1 грн. обеспечит сумму ди≠видендов (250 Ј 1) / 100 = 2,5 грн. ћинимально необходима€ норма при≠были по другим инвестици€м составл€ет r = 0,25 (т.е. 25 %).
“огда реальна€ рыночна€ цена акции в текущем году составит:
 .
.
“аким образом, реальна€ цена акции выше предполагаемой цены продажи на 8,72 / 5 = 74,4 %, поэтому покупать акцию за 5 грн. целесо≠образно.
–ыночна€ цена акции, дивиденды по которой имеют посто€нную тенденцию к росту, определ€етс€ по формуле:
 ,
,
где  Ц рыночна€ цена акции в текущем году, грн.;
Ц рыночна€ цена акции в текущем году, грн.;
 Ц последние выплаченные дивиденды, грн.;
Ц последние выплаченные дивиденды, грн.;
|
|
|
d Ц ожидаемый темп роста дивидендов, в дол€х ед.;
r Ц минимально необходима€, по мнению инвестора, норма прибыли, которую он может получить по другим инвестици€м (дисконт), в дол€х единицы.
примеру, инвестор владеет акцией, номинал которой 1 грн., по которой он получил в прошлом году дивиденды в размере 180 % годовых, или (180 Ј 1) / 100 = = 1,8 грн. на одну акцию в 1 гривню. јнализ данных за последние два года показал, что среднегодовой темп роста дивидендов составл€ет 40 %. ћинимально необходима€ норма прибыли по другим инвестици€м Ц 0,65.
–ыночна€ цена данной акции составит:
 .
.
ѕоэтому инвестор может продать акцию не менее чем за 10,08 грн.
ќпределение рыночной цены привилегированной акции, котора€ выпускаетс€ с фиксированным размером дивидендов, привилегированной акции, котора€ выпускаетс€ с фиксированным размером дивидендов, производитс€ по формуле:
 ,
,
где  Ц рыночна€ цена привилегированной акции в текущем году, грн.;
Ц рыночна€ цена привилегированной акции в текущем году, грн.;
r Ц минимально необходима€, по мнению инвестора, норма прибыли, которую он может получить по другим инвестици€м, в дол€х единицы%
ƒ Ц установленный размер дивиденда по привилегированной акции, грн.
примеру, инвестор купит привилегированную акцию за 3,5 грн., номинал которой Ц 1 грн. ”становленный размер дивиденда по ней Ц 250 % годовых, т. е. (250 Ј 1) / 100 = 2,5 грн. ћинимально необходима€ норма прибыли по другим инвестици€м Ц 0,65. “огда рыночна€ цена данной акции составл€ет 2,5 / 0,65 = 3,85 грн., т.е. инвестор купил еЄ с выгодой дл€ себ€ по цене ниже реальной рыночной стоимости на 3,5 Ц 3,85 = 0,35грн. или на (3,5 / 3,85) Ј 100 Ц Ц100 = Ц 29,87 %.






