“ема 10. „исельн≥ методи оптим≥зац≥њ
ѕостановка задач≥
«адача оптим≥зац≥њ - одна ≥з найважлив≥ших задач, що зустр≥чаютьс€ в практиц≥ наукових, ≥нженерних та економ≥чних досл≥джень теоретичного та прикладного характеру.
ѕроблеми оптим≥зац≥њ виникають:
- п≥д час керуванн€ р≥зними технолог≥чними процесами, агрегатами, установками, де потр≥бно дос€гти максимальноњ продуктивност≥ прац≥ за умови найкращоњ €кост≥ та м≥н≥мальних затрат;
- п≥д час проектуванн€ р≥зних ≥нженерних конструкц≥й, пристроњв, схем, коли потр≥бно п≥д≥брати таку комб≥нац≥ю њх параметр≥в, €ка б за м≥н≥мальноњ матер≥алом≥сткост≥ в≥дпов≥дала б найкращим експлуатац≥йним характеристикам проектованого обТЇкта;
- п≥д час створенн€ нових зразк≥в продукц≥њ, коли синтезуютьс€ х≥м≥чн≥ сполуки з найкращими заданими €кост€ми тощо.
ѕри постановц≥ задач≥ оптим≥зац≥њ, система оптим≥зац≥њ зам≥нюЇтьс€ њњ моделлю (рисунок 34).
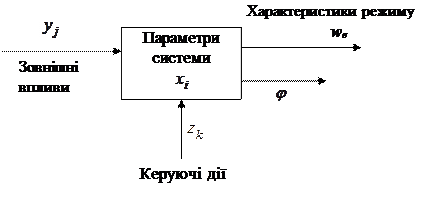 |
–исунок 34 Ц ћодель техн≥чноњ системи
“ака модель маЇ параметри 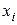 , зазнаЇ зовн≥шн≥х вплив≥в
, зазнаЇ зовн≥шн≥х вплив≥в 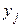 , п≥дкор€Їтьс€ керуючим д≥€м
, п≥дкор€Їтьс€ керуючим д≥€м 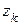 та маЇ характеристики режима
та маЇ характеристики режима 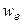 , €к≥ залежать в≥д
, €к≥ залежать в≥д 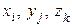 . ќдна ≥з характеристик режима j називаЇтьс€ критер≥Їм оптимальност≥. «адача оптим≥зац≥њ заключаЇтьс€ в тому, щоб вибрати так≥ керуючи д≥њ
. ќдна ≥з характеристик режима j називаЇтьс€ критер≥Їм оптимальност≥. «адача оптим≥зац≥њ заключаЇтьс€ в тому, щоб вибрати так≥ керуючи д≥њ 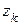 , при €ких критер≥й оптимальност≥ давав би екстремальн≥ значенн€ (max або min). ’арактеристику j ще називають ц≥льовою функц≥Їю.
, при €ких критер≥й оптимальност≥ давав би екстремальн≥ значенн€ (max або min). ’арактеристику j ще називають ц≥льовою функц≥Їю.
¬ задачах конструюванн€ оптим≥зуютьс€ параметри системи 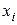 , а в д≥ючих обТЇктах ≥ процесах оптим≥зуютс€ характеристики режиму
, а в д≥ючих обТЇктах ≥ процесах оптим≥зуютс€ характеристики режиму 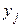 .
.
¬ багатьох прикладних задачах виб≥р параметр≥в системи 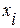 не може бути дов≥льним. ¬ звТ€зку з цим задач≥ оптим≥зац≥њ под≥л€ютьс€ на 2 типи: безумовн≥ та умовн≥.
не може бути дов≥льним. ¬ звТ€зку з цим задач≥ оптим≥зац≥њ под≥л€ютьс€ на 2 типи: безумовн≥ та умовн≥.
Ѕезумовн≥ задач≥ Ц це задач≥ без обмежень на зм≥нн≥ 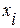 . –озвТ€занн€ њх пол€гаЇ в знаходженн≥ екстремуму ц≥льовоњ функц≥њ
. –озвТ€занн€ њх пол€гаЇ в знаходженн≥ екстремуму ц≥льовоњ функц≥њ 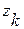 , що найчаст≥ше реал≥зуЇьс€ класичними методами математичного анал≥зу (спуск, по антиград≥Їнту, найшвидший спуск, випадковий спуск, спуск по антиград≥Їнту з оптим≥зац≥Їю кроку та ≥нш≥).
, що найчаст≥ше реал≥зуЇьс€ класичними методами математичного анал≥зу (спуск, по антиград≥Їнту, найшвидший спуск, випадковий спуск, спуск по антиград≥Їнту з оптим≥зац≥Їю кроку та ≥нш≥).
¬ умовних задачах оптим≥зац≥њ на зм≥нн≥ 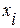 накладаЇтьс€ обмеженн€ в вигл€д≥ р≥вностей або ер≥вностей, що встановлюютьс€ ≥з ф≥зичних м≥ркувань. ожне обмеженн€ д≥лить прост≥р на допустим≥ ≥ недопустим≥ п≥дпростори. “а множина точок n -вим≥рного простору, €ка задовольн€Ї обмеженн€ задач≥, називаЇтьс€ областю допустимих розвТ€зк≥в.
накладаЇтьс€ обмеженн€ в вигл€д≥ р≥вностей або ер≥вностей, що встановлюютьс€ ≥з ф≥зичних м≥ркувань. ожне обмеженн€ д≥лить прост≥р на допустим≥ ≥ недопустим≥ п≥дпростори. “а множина точок n -вим≥рного простору, €ка задовольн€Ї обмеженн€ задач≥, називаЇтьс€ областю допустимих розвТ€зк≥в.
«алежно в≥д виду ц≥льовоњ функц≥њ та функц≥њ обмежень розр≥зн€ють задач≥ л≥н≥йного, нел≥н≥йного, динам≥чного, стохастичного програмуванн€.
ласична задача отриманн€ оптимальних план≥в зводитьс€ до такого:
1) задана де€ка функц≥€ 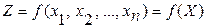 (10.1)
(10.1)
дл€ €коњ потр≥бно знайти максимум (м≥н≥мум);
2) множина параметр≥в системи ’ задаЇтьс€ з допомогою системи р≥вн€нь та нер≥вностей; 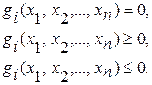 (10.2)
(10.2)
“ак≥ задач≥ або не розвТ€зуютьс€ класичними методами взагал≥, або застосуванн€ њх приводить до дуже великоњ трудоЇмкост≥. ѓх розв€зок зд≥йснюЇтьс€ методами математичного програмуванн€. якщо (10.1) Ц л≥н≥йна функц≥€, то це робитьс€ засобами л≥н≥йного програмуванн€. якщо (10.1) або (10.2) мають нел≥н≥йност≥, то так≥ задач≥ розвТ€зуютьс€ методами динам≥чного програмуванн€.
|
|
|
якщо розвТ€зок такоњ задач≥ потребуЇ ц≥лих значень ’, дл€ њх отриманн€ застосовують дискретне програмуванн€.
≤нколи при створенн≥ математичноњ модел≥ необх≥дно врахувати р€д невизначених фактор≥в. ¬ цьому випадку застосовують методи стохастичного програмуванн€.
ѕостановка задач≥ л≥н≥йного програмуванн€
«адача л≥н≥йного програмуванн€ («Ћѕ) формулюЇтьс€ так:
«найти вектор 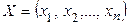 , що м≥н≥м≥зуЇ функц≥ю
, що м≥н≥м≥зуЇ функц≥ю
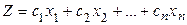
при таких обмеженн€х:
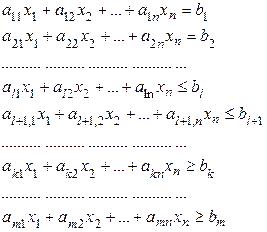 (10.3)
(10.3)
якщо вс≥ обмеженн€ позначаютьс€ знаком дор≥внюЇ, вс≥ значенн€  , а дл€
, а дл€  знаход€ть м≥н≥мум, то така модель називаЇтьс€ канон≥чною. ¬она маЇ вигл€д:
знаход€ть м≥н≥мум, то така модель називаЇтьс€ канон≥чною. ¬она маЇ вигл€д:
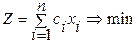
при обмеженн€х:
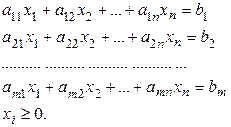 (10.4)
(10.4)
ћодель (10.3) можна привести до канон≥чноњ форми (10.4), скориставшись твердженн€ми:
a) 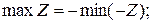
b) 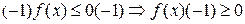 ;
;
c) розвТ€зок системи (10.3) з в≥дТЇмними значенн€ми 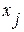 можна звести до системи (10.4) з нев≥дТЇмними
можна звести до системи (10.4) з нев≥дТЇмними 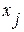 , €кщо в≥дТЇмн≥ компоненти вектора ’ зам≥нити р≥зницею двох додатн≥х:
, €кщо в≥дТЇмн≥ компоненти вектора ’ зам≥нити р≥зницею двох додатн≥х: 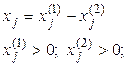
d) €кщо 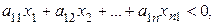 то його можна зам≥нити на р≥вн≥сть шл€хом додаванн€ в л≥ву частину нев≥дТЇмноњ зм≥нноњ
то його можна зам≥нити на р≥вн≥сть шл€хом додаванн€ в л≥ву частину нев≥дТЇмноњ зм≥нноњ 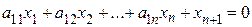 .
.
анон≥чна модель в матричн≥й форм≥ маЇ вигл€д: 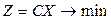 при обмеженн€х
при обмеженн€х 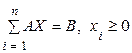 .
.






