«адача прикладу розвТ€зувалась в двовим≥рному простор≥. ќбласть обмежень представл€ла собою пТ€тикутник, в одному ≥з кут≥в €кого одержали точку максимума.
якщо розвТ€зувати задачу з трьома нев≥домими, область розвТ€зку буде многогранником, в одному ≥з кут≥в €кого буде знаходитись оптимальне р≥шенн€. якщо ж задача розвТ€зуЇтьс€ в  вим≥рному простор≥, областю обмежень Ї г≥пермногогранник Ц симплекс. «в≥дси походить назва методу.
вим≥рному простор≥, областю обмежень Ї г≥пермногогранник Ц симплекс. «в≥дси походить назва методу.
¬ибравши де€кий базис перетворимо систему обмежень ≥ ц≥льову функц≥ю в канон≥чну форму


≤з ц≥Їњ системи створюЇмо таблицю:
| Ѕазис | 
| 
| Е | 
| 
| Е | b |

| 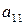
| 
| Е | Е | b1 | ||

| 
| 
| Е | Е | b2 | ||
| Е | Е | Е | Е | Е | Е | Е | |

| 
| 
| Е | Е | bm+n | ||
| Z | 
| 
| Е | Е | b0 | ||

| 
|
Ѕазис в≥дпов≥даЇ кожному куту симплекса. ѕерша таблиц€ в≥дпов≥даЇ початку координат. ќстанн≥й р€док таблиц≥ (без b0) в≥дпов≥даЇ значенню базисних зм≥нних дл€ в≥дпов≥дного кута симплекса. ¬ ком≥рц≥ b0 знаходитьс€ значенн€ ц≥льовоњ функц≥њ при базисному розвТ€зку.
≤де€ розвТ€зку «Ћѕ Ц перевести незалежн≥ зм≥нн≥ в базис, користуючись наступними критер≥€ми.
ритер≥й допустимост≥ базиса:
€кщо в останньому стовпц≥ симплекс-таблиц≥ немаЇ в≥дТЇмних елемент≥в кр≥м, можливо, останнього, то в≥дпов≥дний ц≥й таблиц≥ базис допустимий ( ).
).
ритер≥й оптимальност≥ таблиц≥:
€кщо в останньому р€дку немаЇ додатн≥х елемент≥в, кр≥м, можливо, останнього, то в≥дпов≥дний ц≥й таблиц≥ базис оптимальний ( ). ѕри цьому
). ѕри цьому  .
.
ритер≥й в≥дсутност≥ розвТ€зку:
€кщо в симплекс-таблиц≥ маЇмо такий стовпець, останн≥й елемент €кого додатн≥й, а вс≥ ≥нш≥ недодатн≥, то в≥дпов≥дна «Ћѕ не маЇ оптимального розвТ€зку ( )
)  .
.

ритер≥й ≥снуванн€ ведучого елемента:
€кщо дл€ даноњ симплекс-таблиц≥ не задовольн€Їтьс€ критер≥й оптимальност≥ базиса та в≥дсутност≥ оптимального розвТ€зку, то в ц≥й симплекс-таблиц≥ ≥снуЇ ведучий елемент. …ого знаход€ть в стовпц≥ з найб≥льшим  серед множини
серед множини  по умов≥
по умов≥  .
.
“епер сформулюЇмо алгоритм правил перетворенн€ симплекс-таблиц≥;
1) вс≥ елементи р€дка, на €кому розм≥щений ведучий елемент, д≥лимо на нього (на м≥сц≥ ведучого елемента зТ€вл€Їтьс€ 1);
2) вс≥ ≥нш≥ елементи ведучого стовпц€ зам≥н€Їмо нул€ми;
3) вс≥ ≥нш≥ елементи симплекс-таблиц≥ перетворюЇмо по правилу пр€мокутника:



“епер метод посл≥довного покращенн€ плану або симплекс-метод можна представити так:
1) знаходимо будь-€ке базисне р≥шенн€ ≥ складаЇмо симплекс-таблицю, в≥дпов≥дну цьому базису;
2) перегл€даЇмо останн≥й р€док таблиц≥, €кщо в ньому немаЇ додатн≥х елемент≥в (кр≥м, можливо  ) то оптимальне р≥шенн€ знайдено Ц
) то оптимальне р≥шенн€ знайдено Ц  буде м≥н≥мальним значенн€м
буде м≥н≥мальним значенн€м  ;
;
3) €кщо ж серед елемент≥в останнього р€дка Ї додатн≥ елементи, але хоча б над одним ≥з них Ї стовпець, що не вм≥щуЇ ≥нших додатн≥х елемент≥в, то система немаЇ розвТ€зку;
4) €кщо обидва критер≥њ (пункти 2, 3) не виконан≥, то вибирають ведучий елемент ≥ перетворюють симплекс-таблицю.
|
|
|
ѕерейдемо до розрахунку попереднього прикладу.

—кладемо першу симплекс-таблицю:
| Ѕазис | 
| 
| 
| 
| 
| 
|

| ||||||

| ||||||

| ||||||

|
«находимо ведучий елемент в стовпц≥ 

«начить, ведучий елемент  . ѕо в≥дношенню до нього перетворюЇмо таблицю:
. ѕо в≥дношенню до нього перетворюЇмо таблицю:
| Ѕазис | 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
|
÷€ ж таблиц€ п≥сл€ виконанн€ арифметичних д≥й:
| Ѕазис | 
| 
| 
| 
| 
| 
|

| 3,75 | -0,25 | ||||

| 0,625 | 0,125 | ||||

| 2,875 | -0,625 | ||||

| 8,75 | -6,25 | -2500 |
¬ нов≥й таблиц≥ в останньому р€дку Ї додатн≥й елемент  .
.
Ќад ним знаходимо ведучий елемент таблиц≥ 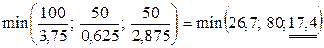 .
.
«начить, ведучим елементом Ї  .
.
ѕовторюЇмо перетворенн€ таблиц≥:
| Ѕазис | 
| 
| 
| 
| 
| 
|

| 1,105 | -1,304 | 34,78 | |||

| 0,261 | 0,217 | 39,13 | |||

| -0,217 | 0,348 | 17,39 | |||

| -7,438 | -3,043 | -2640 |
“аблиц€ оптимальна. ¬ н≥й в≥дпов≥дь:  .
.






