Показники варіації, техніка їх обчислення та економічний зміст

 

Абсолютні показники варіації

 

Назва показника варіації	Формули показників варіації
для незгрупованих даних	для згрупованих даних
Розмах варіації: це різниця між найбільшим і найменшим значеннями варіюючої ознаки	R = χmax - χmin
Середнє лінійне відхилення: це середня з абсолютних відхилень усіх варіантів від середнього значення варіюючої ознаки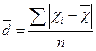
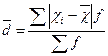
Середній квадрат відхилень (дисперсія): – це середній квадрат відхилень всіх значень ознаки від її середньої величини.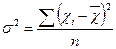
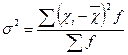
Середнє квадратичне відхилення): це показник, що характеризує середнє коливання ознаки в сукупності, зумовлене індивідуальними особливостями одиниць сукупності.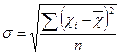

 

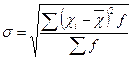
Коефіцієнти варіації

 

лінійний	квадратичний	осциляції

 

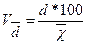
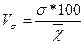
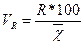
Розрізняють такі значення квадратичних коливань:

V < 10% - незначне коливання

V = від 10% до 30% - середнє коливання

V > 30% - велике коливання

 

Приклад.(для незгрупованих даних) Наведені дані про обсяг виготовленої продукції робітниками за зміну:

Порядковий номер робітника	Обсяг виготовленої продукції за зміну, шт.
Бригада № 1	Бригада № 2
1 2 3 4 5	2 3 12 15 18	8 9 10 11 12
Разом	50	50

Необхідно за допомогою показників варіації дати оцінку продуктивності праці робітників двох бригад.

Розв’язок:

Перш за все визначимо середній випуск продукції робітниками цеху № 1 та № 2.

Середній обсяг виготовленої продукції за зміну	Бригада № 1	Бригада № 2

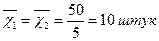
Середній рівень продуктивності праці в обох бригадах однаковий, проте відхилення виробітку окремих членів бригади від середнього показника – різне.

Для характеристики розмірів коливань ознаки по відношенню до середньої величини обчислимо показники варіації. Для здійснення обчислень побудуємо робочу таблицю:

Порядковий номер робітника	Обсяг виготовленої продукції за зміну, шт	Відхилення
Бригада 1	Бригада 2
Бригада 1	Бригада 2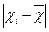
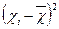
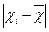
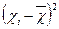
1 2 3 4 5	2 3 12 15 18	8 9 10 11 12
Разом	50	50

Назва показника варіації	Бригада 1	Бригада 2
Розмах варіації: R = χmax - χmin	R=18-2= 16 шт.	R=12-8= 4 шт.
Середнє лінійне відхилення: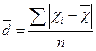
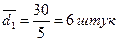
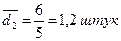
Таким чином, індивідуальні значення виробітку продукції окремих робітників мають такі відхилення від середнього виробітку: у першій бригаді 6 штук, у другій – 1,2 штук. Отже, за показником виробітку продукції за зміну, друга бригада однорідніша за першу.
Середній квадрат відхилень (дисперсія):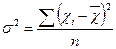
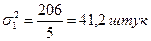
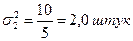
Середнє квадратичне відхилення):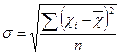

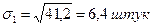
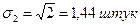
Середнє квадратичне відхилення є «мірилом» надійності середньої. Чим менше середнє квадратичне відхилення, тим об'єктивніше середня арифметична відображує всю сукупність.

Як видно з розрахованих показників, у другій бригаді дисперсія і середнє квадратичне відхилення набагато менші, ніж у першій, що свідчить про високу надійність середньої у другій бригаді.

Обчислюємо відносні показники варіації у наведеному прикладі:

Коефіцієнти варіації	1 бригада	2 бригада
квадратичний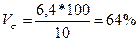

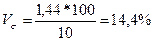
Квадратичний коефіцієнт варіації у першій бригаді дорівнює 64%, що свідчить про досить значні коливання індивідуальних значень змінного виробітку робітників відносно середнього виробітку в цілому по бригаді, тобто сукупність робітників першої бригади за рівнем продуктивності праці якісно неоднорідна, і відповідно, типовість середньої величини виробітку у цій бригаді невелика. У другій бригаді цей показник становить 14,4%, що свідчить про середні коливання середнього виробітку і сукупність робітників цієї бригади за рівнем продуктивності праці досить однорідна.

 

Приклад (для згрупованих даних) В таблиці наведені дані про стаж роботи робітників підприємства:

Стаж роботи, роки	до 5	5-10	10-15	15-20	20 і більше	Разом
Кількість робітників, осіб	18	46	20	10	6	100

Розрахувати показники варіації, на підставі отриманих показників зробити висновки.

Розв’язок:

Вихідні дані є згрупованими. Оскільки відомі значення варіанти (стаж роботи) і частоти (чисельність робітників), то для обчислення середнього стажу роботи використовуємо формулу середньої арифметичної зваженої.

Для обчислення середньої арифметичної в інтервальному ряді розподілу спочатку визначаємо центри заданих інтервалів стажу роботи.

Оскільки у невідома нижня межа першого інтервалу і верхня межа п’ятого інтервалу, то ми їх умовно вважаємо за розміром сусіднього інтервалу. За розрахунковими даними обчислюємо середній стаж.

 

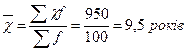
Середній стаж роботи робітників підприємства становить 9,5років.

Для здійснення обчислень показників варіації побудуємо робочу таблицю:

Стаж роботи	Кількість робітників, f	Розрахункові показники
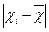
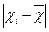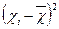
хі	хіf		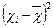f		f
До 5	18	2,5	45	7	126	79	1422
5-10	46	7,5	345	2	92	4	184
10-15	20	12,5	250	3	60	9	180
15-20	10	17,5	175	8	80	64	640
20 і більше	6	22,5	135	13	78	169	1014
Разом	100	-	950	-	436	-	3440

 

Для визначення міри коливань стажу роботи окремих робітників відносно середнього стажу роботи в цілому по підприємству обчислюємо за формулами показники варіації:

Назва показника варіації
Розмах варіації: R = χmax - χmin	R = χmax - χmin = 22,5 – 2,5 = 20 років
Середнє лінійне відхилення: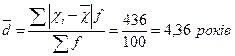
Середній квадрат відхилень (дисперсія):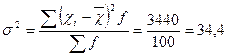
Середнє квадратичне відхилення):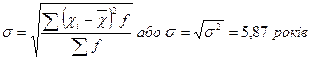
Квадратичний коефіцієнт варіації: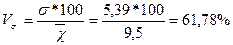

Висновок: таким чином, середній стаж роботи робітників даного підприємства становить 9,5 років. Стаж роботи окремих робітників відрізняється від середнього показника на 4,36 років за середнім лінійним відхиленням і на 5,39 років за середнім квадратичним відхиленням. Коефіцієнт варіації 56,7% свідчить про значні коливання стажу роботи окремих робітників по відношенню до середнього стажу роботи на підприємстві, а це означає, що сукупність робітників підприємства за стажем роботи не можна вважати якісно однорідною. Відповідно, обчислений показник середнього стажу роботи не буде типовим для робітників цього підприємства, оскільки індивідуальні значення стажу роботи мають значні коливання і суттєво відрізняються від середнього стажу роботи.

 

Види дисперсій

 

 

Назва показників варіації	Формули
для незгрупованих даних	для згрупованих даних
Загальна дисперсія характеризує варіацію ознаки під впливом усіх умов і причин, що зумовили цю варіацію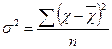
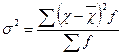
Групова дисперсія дорівнює середньому квадрату відхилень окремих значень ознаки всередині групи від середньої арифметичної відповідної групи.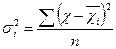
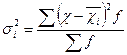
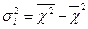
Середня з групових дисперсій: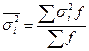
Міжгрупова дисперсія це середній квадрат відхилень групових середніх від загальної середньої.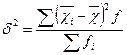
Між наведеними видами дисперсій існує певне співвідношення: загальна дисперсія дорівнює сумі середньої з групових дисперсій та міжгрупової дисперсії.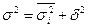

Питання для самоконтролю:

1. Що таке варіація ознак? Наведіть приклади.

2. Які показники використовують для вимірювання варіації? Назвіть їх і наведіть формули.

3. Які недоліки притаманні розмаху варіації і середньому лінійному відхиленню?

4. Розкажіть про дисперсію і середнє квадратичне відхилення та їх місце у системі показників варіації.

5. Назвіть основні математичні властивості дисперсії. Назвіть формули спрощених розрахунків дисперсії і поясніть їх суть.

6. Як вимірюють варіацію альтернативної ознаки?

7. Які види дисперсій ви знаєте? Розкрийте їх суть.

8. Розкажіть про правило додавання (розкладання) варіації. Де воно застосовується?

9. Що таке структурні середні?

10. Дайте визначення моди і медіани. Наведіть їх формули.

11. Як визначають моду і медіану в дискретних та інтервальних рядах розподілу?

12. Як визначають квартилі та децилі?