| Мода | значення ознаки (варіанти) котра частіше за все зустрічається в досліджуваній сукупності (тобто варіанта яка має найбільшу частоту) |
| Медіана | значення варіанти, розташованої в середні упорядкованого ряду розподілу і розділяє цей ряд на дві рівні частини (центр розподілу). |
Способи розрахунку моди залежать від характеру вихідних даних.
| В дискретному ряді розподілу | модою є варіанта, яка має найбільшу частоту | |
| В інтервальному ряді розподілу |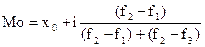 
Примітка: Модальний інтервал визначається за графою частот: інтервал, що відповідає найбільшій частоті, і є модальним.
| x0 – нижня межа модального інтервалу. i – величина інтервалу. f2 – частота модального інтервалу, f1 – частота інтервалу, що передує модальному; f3 – частота позамодального інтервалу (того, що йде після модального інтервалу) |
Приклад (в дискретному ряді розподілу): припустимо, що 9 робітників бригади мають наступні тарифні розряди: 4 3 4 5 3 3 6 2 6.
Приклад (в інтервальному ряді розподілу)
РОЗПОДІЛ ДОМОГОСПОДАРСТВ МІСТА ЗА РІВНЕМ ЗАБЕЗПЕЧЕНОСТІ ЖИТЛОМ
| Житлова площа на одного члена домогосподарства, м2 | Кількість домогосподарств fj | Кумулятивна частка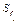 
|
| До 5 | 17 | 17 |
| 5 — 7 | 39 | 56 |
| 7 — 9 | 51 | 107 |
| 9 — 11 | 42 | 149 |
| 11 — 13 | 29 | 178 |
| 13 — 15 | 15 | 193 |
| 15 і більше | 7 | 200 |
| Разом | 200 | ´ |
За даними таблиці модальним є інтервал 7 — 9, що має найбільшу частоту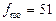 
; ширина модального інтервалу i = 2; нижня межа х0 = 7; передмодальна частота 
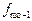= 39, післямодальна — 
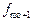= 42. За такого співвідношення частот модальне значення забезпеченості населення житлом:
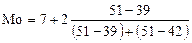= 8,1 м2.
Способи розрахунку медіани залежать від характеру вихідних даних
| В дискретному ряді розподілу | 1. розташувати всі варіанти в зростаючому або спадаючому порядку.
2. медіана знаходиться за її порядковим номером.
| |||
| В інтервальному ряді розподілу |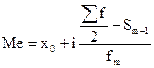 
Примітка: Медіанний інтервал визначається за графою частот: інтервал, що відповідає1/2 кумулятивних частот.
| x0 – це нижня межа медіанного інтервалу; i – величина інтервалу; Sm-1 – сума накопичених частот до медіанного інтервалу; fm – частота медіанного інтервалу. |
Приклад(в дискретному ряді розподілу). Маємо дані про розподіл дев’яти деталей за їх масою.
| Номер деталі | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Маса, г. | 2,6 | 3,4 | 3,3 | 2,7 | 3,0 | 2,9 | 2,8 | 3,1 | 3,2 |
Перегрупуємо деталі за їх масою в зростаючому порядку.
| Номер деталі | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Маса, г. | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 |
Визначаємо номер медіани:
 |
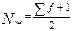Тобто під п’ятим номером від початку або від кінця ряду маса деталі буде
медіаною. Ме = 3,0 г.
Приклад (в інтервальному ряді розподілу)
За даними табл. «РОЗПОДІЛ ДОМОГОСПОДАРСТВ МІСТА ЗА РІВНЕМ ЗАБЕЗПЕЧЕНОСТІ ЖИТЛОМ» половина обсягу сукупності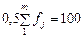 
припадає на інтервал 7 — 9 з частотою
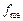= 51; передмедіанна кумулятивна частота 
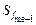= 56. Отже, медіана забезпеченості населення житлом:
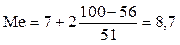м2.
