Час виймання письмової кореспонденції з поштових скриньок в обласних центрах суттєво впливає на значення часу затримки її відправлення, а разом з цим і на строки пересилання.
Можливість оптимізації часу виймання випливає з того, що раннє виймання підвищує ймовірність відправлення письмової кореспонденції в день виймання, але містить малу частину кореспонденції поточного дня, а пізнє – зменшує значення зазначеної ймовірності, але містить велику частину такої кореспонденції.
Задача ставиться так.
В обласному центрі провадиться m виймань письмової кореспонденції В1, В2, … В m, які містять частини q 1, q 2, …, qm добового обміну (q 1+ q 2+ …+ qm = 1).
Відправлення письмової кореспонденції здійснюються n поштовими маршрутами М1, М2, …, М n, які забирають частини Q 1, Q 2, …, Qn добового обміну (Q 1+ Q 2+ …+ Qn = 1).
Задані моменти часу відправлення поштових маршрутів T 1, T 2, …, Tn.
Задані інтервали часу, що витрачається на проведення виймань Δ t в і на оброблення кореспонденції в обласному центрі Δ t о.
Відома статистика заповнення поштових скриньок по годинах доби.
Знайти значення моментів виймання письмової кореспонденції з поштових скриньок t 1, t 2, …, tm, при яких середня затримка відправки письмової кореспонденції з обласного центра набуває мінімального значення.
При розв’язаннізадачі слід враховувати, що виймання кореспонденції з поштових скриньок не може бути виконане одночасно: на проходження маршруту виймання за діючими нормативами виділяється 1,5 год., з яких близько 1,0 год. припадає на проходження частини маршруту від першої до останньої скриньки і близько 0,5 год. – від поштамту до першої скриньки, від останньої скриньки до поштамту та на додаткові операції.
Таким чином, можна вважати, що моменти виймання кореспонденції з поштових скриньок укладаються в інтервал часу, що дорівнює одній годині.
Якщо умовним моментом одночасного виймання з усіх поштових скриньок вважати момент виймання з першої скриньки, то фактичне значення qi буде більше розрахункового; якщо умовним моментом одночасного виймання з усіх поштових скриньок вважати момент виймання з останньої скриньки, то фактичне значення qi буде менше розрахункового.
Для наближення фактичних і розрахункових значень qi доцільно за умовний момент виймання з усіх поштових скриньок узяти середину інтервалу часу проходження маршруту виймання. За такої умови зменшення фактичного значення qi, обумовлене більш раннім вийманням з поштових скриньок на першій частині маршруту виймання, буде компенсуватися збільшенням фактичного значення qi, обумовленим більш пізнім вийманням з поштових скриньок на його другій частині.
Оскільки в складі виймання в загальному випадку присутня кореспонденція поточного і попереднього днів, а з урахуванням інтервалів часу, що витрачається на проведення виймання і оброблення кореспонденції в обласному центрі, її відправлення може здійснюватися поштовими маршрутами поточного або наступного днів, можливі 4 варіанти відправлення кореспонденції:
1. Кореспонденція поточного дня відправляється в день виймання (сьогоднішня кореспонденція – сьогоднішня відправка). Затримка відправлення відсутня.
2. Кореспонденція поточного дня відправляється наступного після виймання дня (сьогоднішня кореспонденція – завтрашня відправка). Затримка відправлення дорівнює одній добі.
3. Кореспонденція попереднього дня відправляється в день виймання (вчорашня кореспонденція – сьогоднішня відправка). Затримка відправлення дорівнює одній добі.
4. Кореспонденція попереднього дня відправляється наступного після виймання дня (вчорашня кореспонденція – завтрашня відправка). Затримка відправлення дорівнює двом добам.
Частки вчорашньої і сьогоднішньої пошти у складі виймань письмової кореспонденції визначаються законом заповнення поштових скриньок і моментами виймань.
Закон заповнення поштових скриньок може бути встановлено експериментально шляхом підрахунку кількості листів, що опускають у поштові скриньки за одиницю часу (звичайно за годину).
На рис.6.5 наведені приклади визначення часток вчорашньої і сьогоднішньої пошти при лінійному законі заповнення поштових скриньок і при наявності одного або двох виймань у різні моменти часу.
D в, D c Виймання о 08.00 
1,0
0,8
0,6
0,4
0,2
D в, D c Виймання о 12.00
1,0
0,8
0,6
0,4
0,2
D в, D c Виймання о 16.00
1,0
0,8
0,6
0,4
0,2
D в, D c Виймання о 18.00
1,0
0,8
0,6
0,4
0,2
D в, D c Виймання о12.00 і о 16.00
1,0
0,8
0,6
0,4
0,2
0 2 4 6 8 10 12 14 16 18 20 22 24 Т
Пошта вчорашнього дня
Пошта сьогоднішнього дня
Рисунок 6.5. Визначення часток вчорашньої і сьогоднішньої пошти
При цьому слід враховувати, що частки пошти вчорашнього і сьогоднішнього днів при вийманнях від 00.00 до 08.00 і при вийманнях від 18.00 до 24.00 співпадають відповідно з частками пошти вчорашнього і сьогоднішнього днів при вийманнях о 08.00 і о 18.00.
Хоча співвідношення значень кількості виймань письмової кореспонденції m і кількості відправлень поштових маршрутів n може бути різним, знаходження оптимального розподілу значень моментів виймання t 1, t 2, …, tm при m ≥ n тривіальне: достатньо вибрати n моментів виймання так, щоб значення часу готовності письмової кореспонденції до відправлення t г1, t г2, …, t г n збігалися зі значеннями моментів часу відправлення поштових маршрутів T 1, T 2, …, Tn, а решту m - n виймань провадити в довільні моменти часу до початку останнього виймання, скажімо так, щоб забезпечити більш-менш рівномірне навантаження сортувальниць письмової кореспонденції.
Отже, розглянемо випадок m < n.
На рис. 6.6 наведено приклад часової діаграми розподілу моментів часу виймання, узгоджених з моментами відправлень поштового транспорту, при m = 3, n = 4. Виймання В1 узгоджене з відправленням М2, виймання В2 – з відправленням М4, виймання В3 – з відправленням М1.
В и й м а н н я
В1 В2 В3
t г3 t 1 t г1 t 2 t г2 t 3
0 Т 1 Т 2 Т 3 Т 4 24
М1 М2 М3 М4
В і д п р а в л е н н я
Рисунок 6.6. Часова діаграма розподілу моментів часу виймання письмової кореспонденції
Час готовності письмової кореспонденції до відправлення t г i визначається значеннями моменту виймання ti та інтервалів часу проведення виймання Δ t в і оброблення кореспонденції Δ t о як
t г i = (ti + Δ t в + Δ t о) mod 24,
тобто,
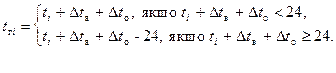
Як випливає з рис.6.6, значення t г1, t г2 визначаються верхнім, а значення t г3 – нижнім рядком виразу t г i .
На рис. 6.7 наведено діаграму розподілу частин q 1, q 2, …, qm добових виймань по частинах Q 1, Q 2, …, Qn добових відправлень.
В1 q 1 Q 1 М1
В i qi Qj М j
В m qm Qn M n
Рисунок 6.7. Діаграма розподілу частин добових виймань письмової кореспонденції
Якщо вважати, що заданий добовий розподіл збігається з розподілом складу кожного виймання, то частина виймання В i, яка відправляється з маршрутом М j, складає qi Qj.
Затримка τ ij відправлення письмової кореспонденції виймання В i поштовим маршрутом М j визначається співвідношенням часу готовності t г i зазначеної кореспонденції до відправлення і часу відправлення Тj зазначеного маршруту
τ 
Отже, при τ ij = 0 кореспонденція виймання В i відправляється маршрутом М j в день виймання, а при τ ij = 1 – наступного після виймання дня.
Маршрути виймання кореспонденції з поштових скриньок в обласних центрах, як правило, не збігаються. Так, в центральних районах, поблизу вокзалів, портів, станцій метрополітену виймання провадяться частіше, ніж в так званих “спальних”, промислових і віддалених районах.
Внаслідок цього, кореспонденція попереднього дня може бути присутня в складі кожного виймання (при співпадінні маршрутів виймання кореспонденція попереднього дня може бути присутня лише в складі першого виймання).
Таким чином, в загальному випадку
qі = q с і + q в і ,
де q с і і q в і – відповідно частини кореспонденції сьогоднішнього і вчорашнього днів у складі виймання В i.
Виходячи з викладеного, значення середньої затримки письмової кореспонденції в обласному центрі складає
.
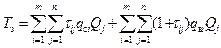Після нескладних перетворень одержимо
.
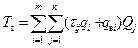За наявності одного виймання
.
Розв’язання задачі оптимізації часу виймання письмової кореспонденції зводиться до мінімізації значення Т з з усіх 
можливих варіантів m виймань, узгоджених з n відправленнями поштових маршрутів
.
У табл. 6.2 наведені результати розв’язання задачі оптимізації часу виймання кореспонденції за такими вихідними даними:
- кількість виймань m = 1,2,3;
- кількість відправлень n = 4;
- час відправлення поштових маршрутів Т 1 = 11.00, Т 2 = 15.00, Т 3 = 20.00, Т 4 = 23.00;
- інтервал часу виймання, год., Δ t в = 1;
- інтервал часу оброблення, год., Δ t 0 = 3;
- частини добового обміну, що відправляються з поштовими маршрутами Q 1 = 0,2; Q 2 = 0,4; Q 3 = 0,1; Q 4 = 0,3;
- закон заповнення поштових скриньок за годинами доби
- маршрути виймання збігаються.
Таблиця 6.2. Результати розв’язання задачі оптимізації часу виймання кореспонденції
| Час виймання | Частини добового обміну в вийманнях | Середня затримка | ||||||||||
| t 1 | t 2 | t 3 | q 1 | q 2 | q 3 | q c1 | q c2 | q c3 | q в 1 | q в 2 | q в 3 | Т з |
| 07.00 | 1,0 | 0,0 | 1,0 | 1,00 | ||||||||
| 11.00 | 1,0 | 0,3 | 0,7 | 0,90 | ||||||||
| 16.00 | 1,0 | 0,8 | 0,2 | 0,80 | ||||||||
| 19.00 | 1,0 | 1,0 | 0,0 | 0,70 | ||||||||
| 07.00 | 11.00 | 0,7 | 0,3 | 0,0 | 0,3 | 0,7 | 0.0 | 0,76 | ||||
| 07.00 | 16.00 | 0,2 | 0,8 | 0,0 | 0,8 | 0,2 | 0,0 | 0,68 | ||||
| 07.00 | 19.00 | 0,0 | 1,0 | 0,0 | 1,0 | 0,0 | 0,0 | 0,70 | ||||
| 11.00 | 16.00 | 0,5 | 0,5 | 0,3 | 0,5 | 0,2 | 0,0 | 0,60 | ||||
| 11.00 | 19.00 | 0,3 | 0,7 | 0,3 | 0,7 | 0,0 | 0,0 | 0,55 | ||||
| 16.00 | 19.00 | 0,8 | 0,2 | 0,8 | 0,2 | 0,0 | 0,0 | 0,62 | ||||
| 07.00 | 11.00 | 16.00 | 0,2 | 0,3 | 0,5 | 0,0 | 0,3 | 0,5 | 0,2 | 0,0 | 0,0 | 0,56 |
| 07.00 | 11.00 | 19.00 | 0,0 | 0,3 | 0,7 | 0,0 | 0,3 | 0,7 | 0,0 | 0,0 | 0,0 | 0,55 |
| 07.00 | 16.00 | 19.00 | 0,0 | 0,8 | 0,2 | 0,0 | 0,8 | 0,2 | 0,0 | 0,0 | 0,0 | 0,62 |
| 11.00 | 16.00 | 19.00 | 0,3 | 0,5 | 0,2 | 0,3 | 0,5 | 0,2 | 0,0 | 0,0 | 0,0 | 0,50 |
Як випливає з табл. 6.2, мінімальні значення середньої затримки письмової кореспонденції мають місце при проведенні виймань:
- однієї – в 19.00 (затримка 0,70);
- двох – в 11.00 і 19.00 (затримка 0,55);
- трьох – в 11.00, 16.00, 19.00 (затримка 0,50).
З табл. 6.2 також видно, що при невдалому виборі моментів виймання, середня затримка при більшій кількості виймань може перевищувати середню затримку при меншій кількості виймань.
