Приклад виконання лабораторної роботи

Задача. Будівельна дільниця має в наявності три групи взаємопов'язаних механізмів (М₁, М₂, М₃). Фонд робочого часу відповідно становить 800, 900 і 600 машино-змін за місяць. Дільниці встановлено план виконання п'яти видів робіт (Р₁, Р₁, Р₃, Р₄, Р₅) в такому обсязі 450,320,640,520 і 280 м³. Норми витрат часу за видами робіт і групами механізмів наведено в табл. 11.4.

Таблиця 11.4

Норми витрат часу на одиницю виконаної роботи

 

Група механізмів	Норми витрат часу на одиницю виконаної роботи відповідним механізмом, машино-змін
Р1	Р2	Р3	Р4	Р5
М1	0,2	0,3	0,5	0,25	0,4
М2	0,4	0,45	0,56	0,6	0,5
М3	0,41	0,65	0,56	0,45	0,3

 

Собівартість одиниці роботи, виконаної відповідною групою механізмів наведено в табл. 11.5.

Таблиця 11.5

Собівартість одиниці виконаної роботи

 

 

Група механізмів	Собівартість одиниці виконаної роботи відповідним механізмом, грн.
Р1	Р2	Р3	Р4	Р5
М1
М2
М3

 

Знайти оптимальний план завантаження будівельних механізмів, який забезпечить мінімальні витрати.

Розв'язок

Для побудови моделі введемо невідому величину х_ij– обсяг і-го виду роботи (j = 1, 2,..., 5), яка виконується і-им механізмом (i = 1, 2, 3).

Цільова функція мінімуму витрат набуде вигляду:

F(х) = 20х₁₁ + 30x₁₂ + 40x₁₃ + 35x₁₄ + 45x₁₅ + 30x₂₁ +... + 55х₃₅ ® min.

За такими обмеженнями:

1) по використанню наявного фонду робочого часу механізмів:

М₁: 0,2х₁₁ + 0,3х₁₂ + 0,5х₁₃ + 0,25х₁₄ + 0,4х₁₅ ≤ 800;

М₂: 0,4х₂₁ + 0,45х₂₂ + 0,56х₂₃ + 0,6х₂₄+ 0,5х₂₅ ≤ 900;

М₃: 0,41х₃₁ + 0,65х₃₂ + 0,56х_ЗЗ + 0,45х₃₄ + 0,Зх₃₅ ≤ 600;

2) по виконанню гарантованого плану відповідних механізованих робіт:

Р₁: х₁₁ + х₂₁ + х₃₁ ≥ 450;

Р₂: х₁₂ + х₂₂ + х₃₂ ≥ 320;

Р₃: х₁₃ + х₂₃ + х_ЗЗ ≥ 640;

Р₄: х₁₄ + х₂₄ + х₃₄ ≥ 520;

Р₅: х₁₅ + х₂₅ + х₃₅ ≥ 280;

3) умова невід'ємності змінних:

х_ij ≥ 0, і=1,2,3; j=1,2,3,4,5.

Розв'язавши дану задачу, бачимо, що всі будівельні роботи будуть виконані в запланованих обсягах.

Висновок. Оптимальний план завантаження механізмів буде такий:

Це свідчить про те, що для того щоб загальна собівартість робіт була мінімальною потрібно:

на першому механізмі виконувати роботу Р₁ в обсязі 450 одиниць і роботу Р₅ в обсязі 280 одиниць;

на другому механізмі – роботу Р₂ – 308,3 одиниць;

на третьому механізмі – роботу Р₂ – 11,7; Р₃ – 640 і Р₄ – 520 одиниць продукції.

 

Лабораторна робота № 12. «Транспортна задача»

 

На практиці при перевезенні вантажів може виникнути одна з трьох ситуацій.

І.

Метою транспортної задачі є таке планування перевезень вантажу від постачальників до споживачів, щоб забезпечити мінімальні транспортні витрати.

Введемо позначення:

х_ij – змінні, які підлягають розшуку та виражають кількість вантажу, який перевозиться від і-го постачальника до j-го споживача (і=1...m, j=1...n);

с_ij – вартість перевезення одиниці вантажу від i -го постачальника до
j -го споживача;

а_i – кількість одиниць вантажу у і-го постачальника;

b_j – кількість одиниць вантажу, яка потрібна j-му споживачу.

Транспортна задача може бути сформульована як частковий випадок задачі лінійного програмування і вирішена симплекс-методом.

Кількість одиниць вантажу у постачальників відповідає попиту з боку споживачів, що відображається в умові балансу

. (12.1)

Така економіко-математична модель транспортної задачі називається закритою та з урахуванням умови (8.1) вона має вид:

; (12.2)

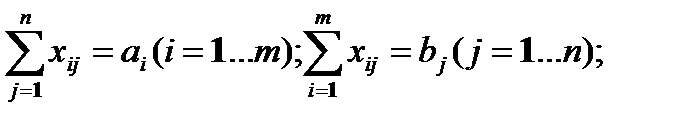(12.3)

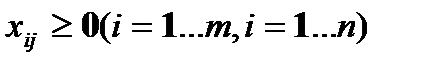. (12.4)

Дана транспортна задача є збалансованою.

У наведених виразах формула (12.2) відповідає цільовій функції з мінімізації транспортних витрат. Формули (12.3) є обмеженнями задачі:

перша формула характеризує те, що весь вантаж від постачальників має бути вивезеним;

друга формула відтворює той факт, що попит споживачів задоволений.

Формула (12.4) є умовою невід'ємності змінних.

ІІ.

Кількість вантажу у постачальників більше попиту у ньому з боку споживачів:

(12.5)

Це означатиме, що частина вантажу у постачальників залишиться, а споживачі отримають весь потрібний їм вантаж. Тому знак у першому обмеженню (12.3) зміниться з "=" на "≥". Інші формули розглянутої моделі (12.2)–(12.4) залишаться такими ж.

ІІІ.

Кількість вантажу у постачальників менше попиту в ньому у споживачів:

(12.6)

Це означатиме, що кожен постачальник увесь свій вантаж вивезе, а частина споживачів отримає вантажу менше відповідної кількості. Тому друге обмеження у формулах (12.3) буде мати знак "≤". Інші формули моделі (12.2)–(12.4) залишаться без зміни.

Економіко-математичні моделі у ситуаціях II і III називаються відкритими, а самі задачі – незбалансованими.

У всіх трьох розглянутих моделях кількість основних змінних складає m´n,
а кількість обмежень – (m+n).

Найбільш простою та часто використовуємою є закрита модель (12.2)–(12.4). З особливостями реалізації відкритих моделей можна познайомитися у спеціальній літературі.