
Ќа баз≥ наведеного математичного опису можна про≥люструвати суть ц≥Їњ модел≥ так: необх≥дно визначити значенн€ n нев≥дТЇмних зм≥нних  , €к≥ задовольн€ють обмеженн€м 3.2та забезпечують екстремальне значенн€ (максимальне або м≥н≥мальне) ц≥льовоњ функц≥њ, €ка виражена р≥вн€нн€м 3.1.
, €к≥ задовольн€ють обмеженн€м 3.2та забезпечують екстремальне значенн€ (максимальне або м≥н≥мальне) ц≥льовоњ функц≥њ, €ка виражена р≥вн€нн€м 3.1.
ƒо метод≥в вир≥шенн€ задач Ћѕ в≥днос€тьс€ граф≥чний метод, симплекс-метод. —имплекс-метод Ї анал≥тичним методом знаходженн€ р≥шенн€ задач Ћѕ.
ѕриклад. √раф≥чним методом розвТ€зати задачу л≥н≥йного програмуванн€:
Z = 3x1+7x2-5 (extr),
4x1 -3х2  12,
12,
10x1 + 13х2 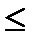 130,
130,
- 6х1 + 8х2 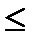 48,
48,
2х1 +5х2  10,
10,
4х1 - х2 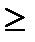 0,
0,
х 1 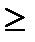 0,
0,
х 2 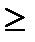 0.
0.
–озв Т€зуванн€.
ЅудуЇмо граничн≥ пр€м≥, €к≥ в≥дпов≥дають нер≥вност€м системи обмежень задач≥ (кожне обмеженн€ розгл€даЇмо €к р≥вн€нн€). ƒл€ побудови дов≥льноњ пр€моњ нам потр≥бно дв≥ точки. якщо права частина р≥вн€нн€ не дор≥внюЇ нулю, то дл€ простоти знаходженн€ координат двох точок, через €к≥ проходить гранична пр€ма (наприклад L1), беремо спочатку x1=0 iзнаходимо х2: 4Ј0Ц3х2=12, зв≥дси Ц 3х2=12, а х2= Ц4. ћи маЇмо координати одн≥Їњ точки (0, -4). ѕот≥м п≥дставл€Їмо х2=0 ≥ визначаЇмо х1: 4х1Ц3 0=12, зв≥дси 4х1=12, а х1=3. ќтже, координати другоњ точки (3,0). јналог≥чно знаходимо координати точок дл€ побудови граничних пр€мих L2, L3 та L4.
¬ прав≥й частин≥ граничноњ пр€моњ, що в≥дпов≥даЇ п'€тому обмеженню - нуль, тому ц€ пр€ма проходить через початок координат, отже координати першоњ точки (0;0). ƒл€ визначенн€ координат другоњ точки беремо дов≥льне значени€ одн≥Їњ з нев≥домих (т≥льки не 0), наприклад, х1=1 ≥ визначаЇмо х 2:  -х2=0, зв≥дси х2= 4
-х2=0, зв≥дси х2= 4
| L1 | 4x1 -3х2 = 12 | (0;-4); | (3;0). |
| L2: | 10x1 + 13х2 = 130 | (0;10); | (13;0). |
| L3 | - 6х1 + 8х2 = 48 | (0;6); | (-8;0). |
| L4: | 2х1 +5х2 = 10, | (0;2); | (5;0). |
| L5 | 4х1 - х2 = 0, | (0;0); | (1;4). |
| L6 | x1 =0, | в≥сь | Ox 2. |
| L7 | х2 =0, | в≥сь | Ox 1. |
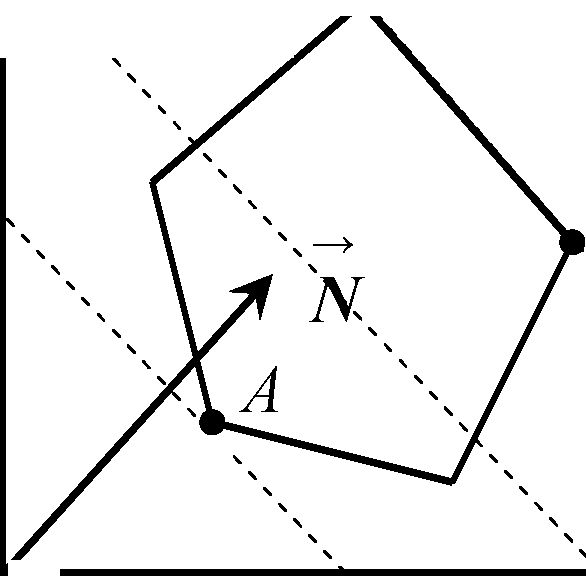
«находимо п≥вплощини розвТ€зк≥в, що в≥дпов≥дають нер≥вност€м системи обмежень. ƒл€ цього беремо дов≥льну точку координатноњ площини, через €ку не проходить гранична пр€ма 4x1 -3х2 = 12 (дл€ простоти розрахунк≥в в≥зьмемо (0,0)) ≥ п≥дставл€Їмо в першу нер≥вн≥сть. ќтримаЇмо 4 0-3 0<12; 0<12, отже, нер≥вн≥сть справджуЇтьс€. ј це значить, що п≥вплощина розвТ€зк≥в, €ка в≥дпов≥даЇ першому обмеженню задач≥, розм≥щена в напр€мку точки (0,0). Ќа рисунку вказуЇмо стр≥лкою, в €кому напр€мку в≥д пр€моњ L1 розм≥щена п≥вплощина розвТ€зк≥в. јналог≥чн≥ розрахунки проводимо з ус≥ма граничними пр€мими. “≥льки дл€ визначенн€ п≥вплощини розвТ€зк≥в, що в≥дпов≥даЇ пТ€тому обмеженню, беремо координати дов≥льноњ точки, що не належить пр€м≥й, т≥льки не точку (0,0), оск≥льки гранична пр€ма L5 проходить через початок системи координат. ЎукаЇмо сп≥льну область, де перетинаютьс€ вс≥ п≥вплощини розвТ€зк≥в. ¬ нашому випадку багатокутником розвТ€зк≥в Ї ф≥гура ABCDE.
ЅудуЇмо вектор нормал≥ 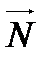 ={(0;0);(3;7)}. ѕерпендикул€рно до нього - л≥н≥ю р≥вн≥в. ѕаралельно переносимо цю л≥н≥ю в напр€мку вектора нормал≥. ќстанньою вершиною багатокутника, €ку перетне л≥н≥€ р≥вн≥в Ї точка — - точка максимуму. “од≥ паралельно переносимо л≥н≥ю р≥вн≥в у напр€мку, протилежному до напр€мку вектора нормал≥. райньою вершиною, €ку перетне л≥н≥€ р≥вн≥в, Ї точка ј - точка м≥н≥муму.
={(0;0);(3;7)}. ѕерпендикул€рно до нього - л≥н≥ю р≥вн≥в. ѕаралельно переносимо цю л≥н≥ю в напр€мку вектора нормал≥. ќстанньою вершиною багатокутника, €ку перетне л≥н≥€ р≥вн≥в Ї точка — - точка максимуму. “од≥ паралельно переносимо л≥н≥ю р≥вн≥в у напр€мку, протилежному до напр€мку вектора нормал≥. райньою вершиною, €ку перетне л≥н≥€ р≥вн≥в, Ї точка ј - точка м≥н≥муму.
|
|
|
C
x 2
D
x1
–исунок 3.1
«найдемо координати оптимальних точок ≥ найб≥льше та найменше значени€ функц≥њ Z. “очка — належить граничним пр€мим L2 та L3, тому њњ координати обчислимо, розвТ€завши систему р≥вн€нь цих граничних пр€мих:
10x1 + 13х2 = 130,
- 6х1 + 8х2 = 48,
–озвТ€зком системи Ї —(2.64; 7.97). ¬изначимо значенн€ ц≥льовоњ функц≥њ в ц≥й екстремальн≥й точц≥ Zmax =Z(C)=58.71.
јналог≥чно визначимо координати точки м≥н≥муму та в≥дпов≥дне значенн€ ц≥льовоњ функц≥њ. “очка ј Ї перетином пр€мих L4 та L5. «апишемо систему в≥дпов≥дних р≥вн€нь та розв'€жемо њњ.
2х1 +5х2 = 10,
4х1 - х2 = 0,
ќтже, ј(0,45; 1,8). Zmm =Z (A) = 8,95.
ѕриклад. —имплексним методом розвТ€зати задачу л≥н≥йного програмуванн€: ƒл€ виготовленн€ двох вид≥в продукц≥њ ѕ1 та ѕ2 використовуютьс€ три види сировини S 1, S 2 та S 3. «апаси сировини, норми витрат сировини на виготовленн€ одиниц≥ продукц≥њ кожного виду та оптова ц≥на одиниц≥ продукц≥њ кожного виду наведен≥ в таблиц≥:
| ¬ид сировини | «апаси сировини | ¬итрати сировини на виготовленн€ одиниц≥ продукц≥њ | |
| ѕ1 | ѕ2 | ||
| S1 | |||
| S2 | |||
| S3 | |||
| ќптова ц≥на одиниц≥ продукц≥њ |
Ќеобх≥дно знайти такий план виробництва, €кий забезпечить найб≥льший сумарний дох≥д.
–озв'€зуванн€. ѕобудуЇмо математичну модель задач≥. Ќехай х1 та х2 - загальна к≥льк≥сть в≥дпов≥дно продукц≥њ ѕ1 та ѕ2; Z - сумарний дох≥д, €кий отримаЇмо в≥д реал≥зац≥њ виробленоњ продукц≥њ. “од≥ математична модель задач≥ матиме вигл€д:
Z = 9х1+ 6х2 (max),
4 x 1 + 5х2 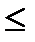 275,
275,
13 x1 + 8х2 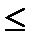 680,
680,
x1 + х2 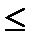 60,
60,
x1 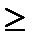 0,
0,
х2  0.
0.
ѕриведемо задачу до канон≥чного виду:
Z = 9х1+ 6х2 (max),
4х1 + 5х2 +х3= 275,
13х1 +8х2 +х4 =680,
х1 + х2 + х5 = 60,
хi 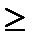 0, i =
0, i = 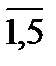 .
.
–озвТ€жемо цю задачу симплекс-методом. «аповнимо початкову таблицю:
“аблиц€ 3.1
| є таблиц≥ | є р€дка | ќпорний план | оеф≥ц≥Їнти при нев≥домих | |||||
| х 1 | х 2 | х 3 | х 4 | х 5 | ||||
| Z | -9 | -6 | ||||||
| х 3 | ||||||||
| x 4 | ||||||||
| х 5 |
≤терац≥€ 1. ¬ нульовий р€док заносимо ≥нформац≥ю про ц≥льову функц≥ю, а в р€дки 1-3 - дан≥ з в≥дпов≥дних р≥вн€нь системи обмежень. ƒл€ заповненн€ нульового р€дка початковоњ симплекс-таблиц≥ ц≥льову функц≥ю запишемо в такому ж вигл€д≥, €к обмеженн€ задач≥, тобто у вигл€д≥ р≥вн€нн€ Z - 9х1 - 6х2 = 0 (вс≥ нев≥дом≥ перенесемо в л≥ву частину), ≥ в подальшому нульовий р€док будемо заповнювати так само, €к ≥ р€дки 1-3, що в≥дпов≥дають обмеженн€м. ¬ стовпчику ЂЅазисї записуЇмо базисн≥ нев≥дом≥ з системи обмежень, а дл€ нульового р€дка базисною нев≥домою Ї Z. ¬ стовпчику Ђќпорний планї записуЇмо значенн€ базисних нев≥домих, коли в≥льн≥ нев≥дом≥ х 1 та х 2 дор≥внюють нулю (прав≥ частини р≥вн€нь-обмежень та ц≥льовоњ функц≥њ). ¬ наступних стовпчиках записуЇмо коеф≥ц≥Їнти при нев≥домих в ц≥льов≥й функц≥њ та систем≥ обмежень.
|
|
|
¬ипишемо з першоњ таблиц≥ початковий опорний план хопорн.= (0; 0; 275; 680; 60). «найдемо значенн€ ц≥льовоњ функц≥њ за цього плану Z (хопорн.) = 9Ј0+6Ј0=0. ѕерев≥римо, чи даний опорний план Ї оптимальним. ƒл€ визначенн€ ступен€ оптимальност≥ опорного плану використовуЇтьс€ нульовий р€док. ÷≥льова функц≥€ досл≥джуЇтьс€ на максимум, значить дл€ оптимальност≥ опорного плану в нульовому р€дку не маЇ бути в≥дТЇмних чисел. ¬ задач≥ в нульовому р€дку Ї два в≥дТЇмних числа ((-9) та (-6)), отже досл≥джуваний опорний план не Ї оптимальним. ¬ибираЇмо найменше з цих чисел (-9). —товпець, в €кому знаходитьс€ це число Ї ключовим, а нев≥дому x 1, €ка в≥дпов≥даЇ цьому стовпцю потр≥бно ввести в базис. —тавимо б≥л€ ц≥Їњ нев≥домоњ стр≥лочку (€кщо ц≥льова функц≥€ м≥н≥м≥зуЇтьс€ ≥ в нульовому р€дку Ї додатн≥ числа, то вибираЇмо найб≥льше з цих чисел ≥ за ним визначаЇмо, €ку нев≥дому потр≥бно ввести в базис). ўоб визначити, €ку з нев≥домих потр≥бно вивести з базису, складаЇмо в≥дношенн€ елемент≥в стовпц€ Ђќпорний планї до в≥дпов≥дних додатних елемент≥в ключового стовпц€ ≥ вибираЇмо найменше з цих в≥дношень:
275: 4 = 68,75;
680:13 = 52,3; (min)
60:l=60.
Ќев≥дому, €ка в≥дпов≥даЇ цьому найменшому в≥дношенню (в нашому випадку х 4) виводимо з базису. ¬≥дм≥чаЇмо цю нев≥дому стр≥лочкою, а р€док, €кому в≥дпов≥даЇ це найменше в≥дношенн€ називаЇтьс€ ключовим. Ќа перетин≥ ключового р€дка ≥ ключового стовпц€ знаходитьс€ ключовий (генеральний) елемент, р≥вний 13.
≤терац≥€ 2. ѕереходимо до другоњ симплекс-таблиц≥. «ам≥сть нев≥домоњ х 4 в базис вводимо нев≥дому x 1. Ќа м≥сц≥ ключового елемента нам потр≥бно отримати 1, а вс≥ ≥нш≥ елементи в стовпц≥ повинн≥ дор≥внювати нулю. ƒл€ цього ключовий р€док д≥лимо на ключовий (генеральний) елемент, тобто на 13, ≥ результат записуЇмо на м≥сц≥ другого р€дка табл. 3.2. ”с≥ ≥нш≥ р€дки табл. 3.2 заповнюЇмо методом ∆ордана-√ауса, посл≥довно виключаючи нев≥дому x 1 з нульового, першого та третього р€дк≥в:
1) множимо вс≥ елементи другого р€дка на 9 ≥ додаЇмо в≥дпов≥дн≥ елементи нульового р€дка табл. 3.1, результат записуЇмо на м≥сц≥ нульового р€дка табл. 3.2;
2) множимо кожен елемент другого р€дка на (Ц4) ≥ додаЇмо в≥дпов≥дн≥ елементи першого р€дка табл. 3.1, результат записуЇмо на м≥сц≥ першого р€дка табл. 3.2;
3) множимо кожен елемент другого р€дка на (Ц1) ≥ додаЇмо в≥дпов≥дн≥ елементи третього р€дка табл. 3.1, результат записуЇмо на м≥сц≥ третього р€дка табл. 3.2.
“аблиц€ 3.2
| є таблиц≥ | є р€дка | ќпорний план | оеф≥ц≥Їнти при нев≥домих | |||||||||
| х 1 | х 2 | х 3 | х 4 | х 5 | ||||||||
| Z | 6120 13 | -6 | 9 13 | |||||||||
| х 3 | 855 13 | 33 13 | -4 13 | |||||||||
| х 1 | 680 13 | 8 13 | 1 13 | |||||||||
| х 5 | 100 13 | 5 | -1 13 | |||||||||
≤з таблиц≥ виписуЇмо новий опорний план:
Xопорн =. 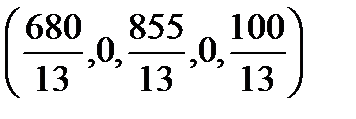
«наченн€ ц≥льовоњ функц≥њ за такого опорного плану
Z(xопорн) = 470.77
ѕерев≥римо цей опорний план на оптимальн≥сть. ¬ нульовому р€дку Ї в≥д'Їмне число (-6/13), тому такий опорний план не Ї оптимальним. Ќев≥дому, €ка в≥дпов≥даЇ цьому стовпцю (х2) вводимо в базис. ¬≥дм≥чаЇмо цю нев≥дому стр≥лочкою. —кладаЇмо в≥дношенн€ елемент≥в стовпц€ Ђќпорний планї до в≥дпов≥дних додатних елемент≥в ключового стовпц€ ≥ вибираЇмо найменше з цих в≥дношень:
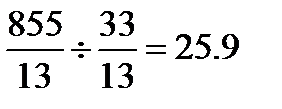
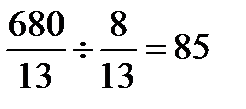
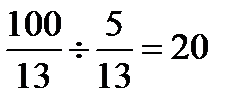 (min).
(min).
Ќев≥дому, €ка в≥дпов≥даЇ цьому найменшому в≥дношенню (в приклад≥ х 5) виводимо з базису. ¬≥дм≥чаЇмо цю нев≥дому стр≥лочкою. лючовий елемент 5/13.
≤терац≥€ 3. ѕереходимо до третьоњ симплекс-таблиц≥. «ам≥сть нев≥домоњ х 5 в базис вводимо нев≥дому х 2. лючовий (трет≥й) р€док д≥лимо на 5/13 ≥ результат записуЇмо на м≥сц≥ третього р€дка табл. 3.3. «нову використаЇмо метод ∆ордана-√ауса, посл≥довно виключаючи нев≥дому х 2з нульового, першого та другого р€дк≥в:
|
|
|
1) множимо вс≥ елементи третього р€дка на 6/13 ≥ додаЇмо в≥дпов≥дн≥ елементи нульового р€дка табл. 3.2, результат записуЇмо на м≥сц≥ нульового р€дка табл. 3.3;
2) множимо кожен елемент третього р€дка на (-33/13) ≥ додаЇмо в≥дпов≥дн≥ елементи першого р€дка табл. 3.2, результат записуЇмо на м≥сц≥ першого р€дка табл. 3.3;
3) кожен елемент третього р€дка множимо на (- 8/13) ≥ додаЇмо в≥дпов≥дн≥ елементи другого р€дка табл. 3.2, результат записуЇмо на м≥сц≥ другого р€дка табл. 3.3.
“аблиц€ 3.3
| є таблиц≥ | є р€дка | Ѕазис | ќпорний план | оеф≥ц≥Їнти при нев≥домих | ||||
| х 1 | х 2 | х 3 | х 4 | х 5 | ||||
| Z | 3 | 6 | ||||||
| х 3 | 1 | -33 | ||||||
| х 1 | 1 | -8 | ||||||
| х 2 | -1 | 13 |
¬ нульовому р€дку останньоњ таблиц≥ немаЇ в≥дТЇмних чисел, це означаЇ на€вн≥сть оптимального розвТ€зку: хопт=(40; 20; 15; 0; 0), Zmax = 480.
ќтже, максимальний дох≥д становитиме Zmax =480, €кщо продукц≥њ ѕ1виготовити 40 одиниць (х1 =40), а продукц≥њ ѕ2 - 20 одиниць (х 2=20).
ѕерев≥рка: Zmax= 9*40 + 6*20 = 360 +120 = 480. Ќев≥дом≥ х 4=0 та х 5=0, а це означаЇ, що сировина S2 та S3 використана повн≥стю, х 3=15, значить сировина S1 Ї в залишку (недовикористана) 15 одиниць.
ѕри розвТ€зуванн≥ задач л≥н≥йного програмуванн€ можлив≥ випадки, коли оптимального плану задач≥ л≥н≥йного програмуванн€ не ≥снуЇ (ц≥льова функц≥€ необмежена) або ≥снуЇ неЇдиний розвТ€зок задач≥
Ћабораторна робота є 6
Ђ«адача оптимального використанн€ ресурс≥вї
«адача. ƒл€ виготовленн€ двох вид≥в продукц≥њ ѕ1 ≥ ѕ2 використовують три види сировини ≤, ≤≤ ≥ ≤≤≤. «апаси сировини, норми њх витрат ≥ прибуток в≥д реал≥зац≥њ одиниц≥ продукц≥њ задано у таблиц≥.
«найти розм≥р максимального прибутку, €кий можна одержати за на€вност≥ даних запас≥в сировини.
¬ар≥анти асортименту обрати з таблиц≥ 6.1.
“аблиц€ 3.4
| N∞ | «атрати ресурс≥в на одиницю продукц≥њ | Ќа€вн≥сть ресурс≥в | ѕрибуток | ||||||||
| ≤ | ≤≤ | ≤≤≤ | |||||||||
| ј1 | ј2 | ј1 | ј2 | ј1 | ј2 | ≤ | ≤≤ | ≤≤≤ | ѕ1 | ѕ2 | |
| 1. | |||||||||||
| 2. | |||||||||||
| 3. | |||||||||||
| 4. | |||||||||||
| 5. | |||||||||||
| 6. | |||||||||||
| 7. | |||||||||||
| 8. | |||||||||||
| 9. | |||||||||||
| 10. | |||||||||||
| 11. | |||||||||||
| 12. | . 80 | ||||||||||
| 13. | |||||||||||
| 14. | |||||||||||
| 15. | |||||||||||
| 16. | |||||||||||
| 17. | |||||||||||
| 18. | |||||||||||
| 19. | |||||||||||
| 20. | |||||||||||
| 21. | |||||||||||
| 22. | |||||||||||
| 23. | |||||||||||
| 24. | |||||||||||
| 25. | |||||||||||
| 26. | |||||||||||
| 27. | |||||||||||
| 28. | |||||||||||
| 29. | |||||||||||
| 30. |
“≈ћј 4. ћќƒ≈Ћ≤ ќѕ“»ћјЋ№Ќќ√ќ ѕЋјЌ”¬јЌЌя Ќј –≤¬Ќ≤ ѕ≤ƒѕ–»™ћ—“¬ј
|
|
|
ќдн≥Їю з основних задач плануванн€ виробництва Ї розрахунок оптимального плану випуску продукц≥њ з урахуванн€м основних фактор≥в, €к≥ впливають на його обс€г.
¬ир≥шенн€ оптим≥зац≥йноњ задач≥ розпод≥л€Їтьс€ на три етапи: побудуванн€ економ≥ко-математичноњ модел≥; находженн€ оптимального р≥шенн€ задач≥; анал≥з результат≥в р≥шенн€.
јсортиментн≥ задач≥ на кондитерських фабриках €вл€ють собою групу задач, в €ких визначають виробничу програму фабрики з урахуванн€м впливу на п≥дприЇмства внутр≥шн≥х фактор≥в (можливостей обладнанн€, л≥м≥т≥в сировини, трудових чинник≥в) та де€ких зовн≥шн≥х вимог (по товарн≥й продукц≥њ в ц≥лому чи окремих њњ асортиментних груп та вид≥в, середньоњ ц≥ни асортименту, €кий випускаЇтьс€).
¬ задач≥ оптим≥зуЇмо виробничу програму п≥дприЇмства по критер≥ю максимального прибутку в≥д реал≥зац≥њ продукц≥њ; в≥дпов≥дно мова п≥де про п≥двищенн€ рентабельност≥ виробництва та зниженн€ соб≥вартост≥.
ƒл€ побудуванн€ абстрактноњ економ≥ко-математичноњ модел≥ асортиментноњ задач≥ введемо наступн≥ умовн≥ позначенн€:
j Ц ≥ндекс виду випускаЇмоњ продукц≥њ;
j = 1, 2,..., n Ц к≥льк≥сть вид≥в випускаЇмоњ продукц≥њ;
xj Ц шукаЇмий випуск продукц≥њ j-того виду;
≥ Ц ≥ндекс виду ведучого обладнанн€;
≥ = 1, 2,..., m Ц к≥льк≥сть одиниць ведучого обладнанн€;
аij Ц звТ€зуючий коеф≥ц≥Їнт обмеженн€ по обладнанню, визначаючий норму витрат часу роботи обладнанн€ ≥ -го виду на випуск одиниц≥ продукц≥њ
j-го виду;
ј≥ Ц потужн≥сть обладнанн€ ≥ -го виду за плановий пер≥од (р≥к);
b Ц соб≥варт≥сть продукц≥њ зв≥тного чи планового року;
Bj Ц питома соб≥варт≥сть j-го виду продукц≥њ;
Dj¢, Dj Ц границ€ попиту на продукц≥ю j-го виду, в≥дпов≥дно верхн≥й ≥ нижн≥й;
pj Ц питомий прибуток в≥д реал≥зац≥њ одиниц≥ продукц≥њ j-го виду;
Sj Ц оптово-в≥дпускна ц≥на одиниц≥ продукц≥њ j-го виду (д≥юча);
S Ц варт≥сть пор≥вн€льноњ товарноњ продукц≥њ зв≥тного чи планового року.
÷≥льова функц≥€ маЇ наступний вигл€д:
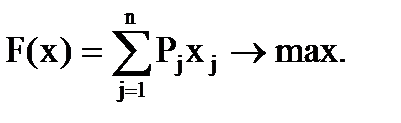
ѕри обмеженн€х:
1. ѕо ведучому обладнанню:
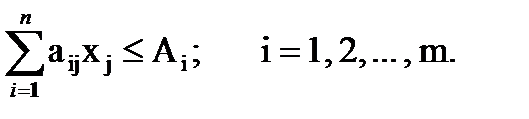
2. ѕо випуску товарноњ продукц≥њ:

3. ѕо попиту на окрем≥ види продукц≥њ:
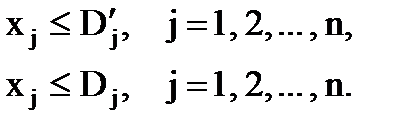
4. ѕо соб≥вартост≥ продукц≥њ:
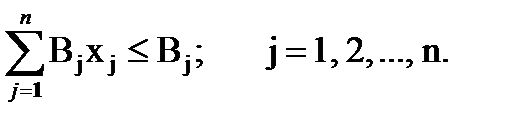
5. ”мова нев≥дТЇмност≥ зм≥нних:
xj ³ 0, j = 1, 2,..., n.
Ћабораторна робота є 7
Ђ–озрахунок оптимальноњ виробничоњ програми карамельного цехуї
«адача. ” карамельному цеху випускають дек≥лька вид≥в продукц≥њ (табл.7.2). ѕродуктивн≥сть л≥н≥й визначаЇтьс€ по варочному апарату. ≥льк≥сть варильних апарат≥в Ц 1.
«адано: оптова ц≥на, соб≥варт≥сть продукц≥њ ≥ попит, р≥чна продуктивн≥сть апарат≥в по карамел≥.
ѕотр≥бно:
1. –озрахувати обс€г ресурс≥в на св≥й асортимент (табл. 7.3).
2. ѕобудувати модель оптимального р≥чного плану п≥дприЇмства у загальному вигл€д≥ по критер≥ю оптим≥зац≥њ Ц максимальний прибуток.
3. «а допомогою отриманих нер≥вностей чи р≥вн€нь побудувати та записати матрицю коеф≥ц≥Їнт≥в ≥ функц≥ю ц≥л≥.
4. ¬ир≥шити задачу за допомогою функц≥њ "ѕоиск решени€" табличного процесора ћicrisoft ≈хсеl.
5. «аповнити вих≥дну таблицю та дати економ≥чний анал≥з.
¬ар≥анти асортименту обрати з таблиц≥ 7.1.
“аблиц€ 7.1
| ’1 | ’2 | ’3 | ’4 | ’5 | |
| ¬ар≥ант 1 | |||||
| ¬ар≥ант 2 | |||||
| ¬ар≥ант 3 | |||||
| ¬ар≥ант 4 | |||||
| ¬ар≥ант 5 | |||||
| ¬ар≥ант 6 | |||||
| ¬ар≥ант 7 | |||||
| ¬ар≥ант 8 | |||||
| ¬ар≥ант 9 | |||||
| ¬ар≥ант 10 |
«г≥дно вар≥анту завданн€ обрати продуктивн≥сть л≥н≥й з таблиц≥ 7.4. ќбрати обмеженн€ по попиту з таблиц≥ 7.5.
|
|
|
“аблиц€ 7.4
| ѕродуктивн≥сть л≥н≥й (т/р≥к) | ||
| Ќепарн≥ вар≥анти | ѕарн≥ вар≥анти: | |
| ¬ар≥ант 1 | ||
| ¬ар≥ант 2 | ||
| ¬ар≥ант 3 | ||
| ¬ар≥ант 4 | ||
| ¬ар≥ант 5 | ||
| ¬ар≥ант 6 | ||
| ¬ар≥ант 7 | ||
| ¬ар≥ант 8 | ||
| ¬ар≥ант 9 | ||
| ¬ар≥ант 10 |
“аблиц€ 7.5
ќбмеженн€ по попиту (т/р≥к)
| ’1 | ’2 | ’3 | ’4 | ’5 | ’6 | ’7 | ’8 | ’9 | |
| max | |||||||||
| min |
“аблиц€ 7.2






