¬заЇмозвТ€зки м≥ж економ≥чними показниками досить часто нос€ть нел≥н≥йний характер ≥ побудована л≥н≥йна модель в такому випадку буде неадекватна реальн≥й д≥йсност≥. Ќел≥н≥йне програмуванн€ використовуЇтьс€ дл€ задач плануванн€ виробництва, управл≥нн€ ресурсами, контролю €кост≥ продукц≥њ.
¬ загальному випадку задача нел≥н≥йного програмуванн€ маЇ вигл€д:
 (4.1)
(4.1)
де  ,
, 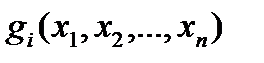 Ц нел≥н≥йн≥ залежност≥ ц≥льовоњ функц≥њ та обмежень.
Ц нел≥н≥йн≥ залежност≥ ц≥льовоњ функц≥њ та обмежень.
ƒл€ розвТ€зуванн€ задач нел≥н≥йного програмуванн€ не ≥снуЇ ун≥версального методу, а тому доводитьс€ застосовувати багато метод≥в та обчислювальних алгоритм≥в, €к≥ в основному ірунтуютьс€ на теор≥њ диференц≥ального численн€, ≥ виб≥р њх залежить в≥д конкретноњ постановки задач≥ та форми економ≥ко-математичноњ модел≥.
ƒо нел≥н≥йних метод≥в знаходженн€ оптим≥зац≥йних р≥шень в≥днос€тьс€: класичний метод оптим≥зац≥њ (за допомогою множник≥в Ћагранжа); метод пр€мого пошуку (град≥Їнтний метод); випукле (квадратичне) програмуванн€; метод уна-“акера, та ≥н.
„асто задачу нел≥н≥йного програмуванн€ намагаютьс€ привести до л≥н≥йного виду, але зам≥на функц≥њ призводить до значних похибок, що зображено на рис. 4.1.

–ис. 4.1. ѕриклад випуклоњ функц≥њ.
¬ точках х1 та х3 значенн€ обох функц≥й сп≥впадають, а в точц≥ х2 в≥др≥зн€ютьс€ значною м≥рою.
ћи бачимо, що л≥неаризац≥€ нел≥н≥йних процес≥в не завжди себе виправдовуЇ ≥ в загальному випадку Ї досить складною математичною задачею.
ѕри розвТ€зуванн≥ нел≥н≥йних задач використовують наближен≥ методи, б≥льш≥сть €ких дають змогу знаходити локальн≥ оптимуми, а вже знайшовши вс≥ локальн≥ оптимуми, методом пор≥вн€нн€ значень ц≥льовоњ функц≥њ у кожн≥й з точок локального оптимуму можна знайти глобальний. Ќаприклад, на рис. 4.2 маЇмо на де€кому в≥др≥зку локальн≥ оптимуми в точках х 1, х 2, х 4, х 5, х 6, х 7, х 9 та х 10, а глобальн≥ Ц в точках х 3 та х 8. ѕроте дл€ практичних розрахунк≥в такий метод не завжди ефективний, тому що часто наближен≥ методи не Ђвловлюютьї глобального оптимуму, особливо коли глобальний оптимум лежить досить близько до локального.

–ис. 4.2. ѕриклад нел≥н≥йноњ функц≥њ.
” задачах л≥н≥йного програмуванн€ точка оптимуму завжди була граничною, а в нел≥н≥йних вона може бути або граничною, або такою, що м≥ститьс€ всередин≥ допустимоњ област≥ розвТ€зк≥в.
ѕитанн€ дл€ п≥дготовки до ≥спиту
1. ќпиш≥ть характерн≥ можливост≥ використанн€ к≥льк≥сних метод≥в в економ≥чних досл≥дженн€х.
2. ƒайте визначенн€ та схематичне зображенн€ к≥льк≥сних метод≥в.
3. ќхарактеризуйте основн≥ складов≥ моделюванн€ соц≥ально-економ≥чних процес≥в.
4. Ќавед≥ть основн≥ визначенн€ деф≥н≥ц≥й Ђмодельї та Ђмоделюванн€ї.
5.ќпиш≥ть основн≥ етапи моделюванн€ та њх характеристики.
6. ≈лементи, €к≥ вход€ть до складу модел≥.
7. ¬изначенн€ основних складових економ≥ко-математичноњ модел≥.
8. ƒисципл≥ни, що складають теоретичну основу математичного моделюванн€. ќпиш≥ть њх структуру.
9. „инники, €кими визначаЇтьс€ вид ≥ характер економ≥ко-математичноњ модел≥.
10.ќзнаки, покладен≥ в основу класиф≥кац≥њ економ≥ко-математичноњ модел≥.
|
|
|
11.ќпиш≥ть €к≥сн≥ характеристики основних економ≥чних моделей.
12.ƒайте схематичну класиф≥кац≥ю математичних моделей.
13.«агальн≥ принципи економ≥ко-математичного моделюванн€.
14.ќхарактеризуйте пон€тт€ концептуальноњ модел≥.
15.ƒл€ €ких ц≥лей будуютьс€ модел≥?
16.ѕредметна область економ≥ко-математичного моделюванн€.
17.–оль функц≥й ≥ граф≥к≥в в економ≥чному моделюванн≥. ѕон€тт€ функц≥ональноњ залежност≥.
18.—пособи завданн€ ≥ досл≥дженн€ функц≥њ. ѕриклади кожного способу.
19.јлгоритм досл≥дженн€ функц≥њ.
20.Ќавед≥ть приклад функц≥њ, €ка описуЇ залеж≥сть величини попиту в≥д доходу.
21.«агальна математична модель задач≥ л≥н≥йного програмуванн€.
22.ƒопустимий розвТ€зок задач≥ л≥н≥йного програмуванн€.
23.ќбласть ≥снуванн€ план≥в.
24.ќпорний план, оптимальний план.
25.≈лементарн≥ модел≥ задач л≥н≥йного програмуванн€.
26.—тандартн≥ форми запису задач л≥н≥йного програмуванн€.
27.як≥ задач≥ л≥н≥йного програмуванн€ можна розвТ€зувати граф≥чним методом?
28.јлгоритм граф≥чного методу розвТ€зуванн€ задач л≥н≥йного програмуванн€.
29.¬изначенн€ опуклоњ множини. ќбмежена множина, необмежена можина.
30.¬изначенн€ внутр≥шньоњ та граничноњ точок множини.
31.—утн≥сть алгоритму граф≥чного методу розвТ€зуванн€ задач л≥н≥йного програмуванн€.
32. анон≥чна форма задач≥ л≥н≥йного програмуванн€.
33.“ипи задач л≥н≥йного програмуванн€, €к≥ можна розвТ€зувати симплексним методом.
34.“еорема про критер≥й оптимальност≥ симплекс-методу.
35.—утн≥сть алгоритму симплексного методу.
36.«адач≥ л≥н≥йного програмуванн€, €к≥ розвТ€зують методом штучного базису. —утн≥сть методу штучного базису.
37.—учасн≥ ≥нформац≥йн≥ технолог≥њ, €к≥ використовуютьс€ дл€ розвТ€зуванн€ задач л≥н≥йного програмуванн€.
38.—формулюйте правила та посл≥довн≥сть побудови двоњстоњ задач≥.
39.ќсновн≥ теореми двоњстост≥.
40.≈коном≥чна ≥нтерпретац≥€ двоњстих оц≥нок.
41.¬изначенн€ деф≥цитност≥ (недеф≥цитност≥) ресурсу ≥з використанн€м двоњстих оц≥нок.
42.¬изначенн€ рентабельн≥сть (нерентабельн≥сть) продукц≥њ ≥з використанн€м двоњстих оц≥нок.
43.¬изначенн€ та постановка транспортноњ задач≥.
44.«акрита та в≥дкрита транспортна задача. «веденн€ в≥дкритоњ транспортноњ задач≥ до транспортноњ задач≥ закритого типу.
45.ћетоди побудови початкового опорного плану транспортноњ задач≥.
46. ритер≥й оптимальност≥ опорного плану транспортноњ задач≥.
47.÷икл перерахунку транспортноњ задач≥. ѕравила перерозпод≥лу продукц≥њ в межах циклу.
48.≈коном≥чн≥ задач≥, що звод€тьс€ до задач транспортного типу. ќднопродуктова задача поточного перспективного плануванн€. ћатематична модель задач≥ оптимального розпод≥лу ф≥нансових ресурс≥в банку. ћатематична модель задач≥ формуванн€ штатного розпису ф≥рми.
49.ѕостановка задач≥ ц≥лочисловою математичного програмуванн€.
50.ѕриклади економ≥чних задач, що належать до класу задач ц≥лочислового л≥н≥йного програмуванн€.
51.ћетоди, що використовують дл€ знаходженн€ оптимального плану ц≥лочисловоњ задач≥. ћетоди в≥дтинанн€. омб≥наторн≥ методи ц≥лочисловоњ оптим≥зац≥њ.
52.—формулюйте постановку та побудуйте математичну модель формуванн€ оптимальноњ ≥нвестиц≥йноњ програми при заданому бюджет≥.
53.«агальна математична модель задач≥ нел≥н≥йного програмуванн€.
54.ѕроблеми, €к≥ виникають при розвТ€зуванн≥ задач нел≥н≥йного програмуванн€.
|
|
|
55.—утн≥сть методу Ћагранжа розвТ€зуванн€ задач нел≥н≥йного програмуванн€. ‘ункц≥€ Ћагранжа.
56.Ќеобх≥дн≥ та достатн≥ умови ≥снуванн€ с≥дловоњ точки дл€ диференц≥йованоњ функц≥њ.
57.ќпукл≥ (ув≥гнут≥) функц≥њ.
58.“еорема уна-“аккера.
59.ћатематична модель задач≥ квадратичного програмуванн€, особливост≥ њњ розвТ€зуванн€.
60.ѕостановка задач≥ динам≥чного програмуванн€.
61.ѕриклади економ≥чних задач, що розвТ€зуютьс€ методами динам≥чного програмуванн€.
62.’арактерн≥ особливост≥ математичноњ модел≥ динам≥чного програмуванн€.
’арактеристика процесу керуванн€ в задачах динам≥чного програмуванн€.
63.’арактерн≥ особливост≥ задач динам≥чного програмуванн€. ѕостановка задач≥ динам≥чного програмуванн€.
64.¬изначенн€ принципу оптимальност≥ Ѕелмана
65.≈коном≥чний зм≥ст рекурентних сп≥вв≥дношень в задачах динам≥чного програмуванн€.
66.ќпиш≥ть економ≥чну ≥ математичну постановку задач≥ оптимального розпод≥лу ф≥нансових ресурс≥в м≥ж ≥нвестиц≥йними проектами.
ƒодаток 1






