‘ункц≥њ в економ≥чному моделюванн≥ використовуютьс€ дл€ визначенн€ ймов≥рних значень результативноњ ознаки при зм≥н≥ керованоњ зм≥нноњ. ƒл€ отриманн€ функц≥њ проводитьс€ статистичне спостереженн€ ≥ збираютьс€ в≥дпов≥дн≥ емп≥ричн≥ значенн€. ƒал≥ висуваЇтьс€ г≥потеза про форму залежност≥ м≥ж досл≥джуваними зм≥нними ≥ використовуЇтьс€ в≥дпов≥дний математичний апарат дл€ визначенн€ параметр≥в р≥вн€нн€ регрес≥њ (модел≥). “еоретичн≥ значенн€, розрахован≥ за моделлю "зам≥нюють" емп≥ричн≥ значенн€. ƒл€ того щоб оц≥нити €к≥сть такоњ зам≥ни необх≥дно розрахувати показники т≥сноти зв€зку (коеф≥ц≥Їнт детерм≥нац≥њ, €кий показуЇ частку залежност≥ вар≥ац≥њ результативноњ ознаки в≥д зм≥ни факторноњ, та коеф≥ц≥Їнт корел€ц≥њ, €кий вказуЇ не т≥льки на т≥сноту, а ≥ на напр€мок зв€зку). ѕ≥сл€ оц≥нки т≥сноти зв€зку необх≥дно переконатис€ в адекватност≥ модел≥ за допомогою статистичних критер≥њв. «наченн€ статистичних критер≥њв розраховують, а пот≥м пор≥внюють ≥з в≥дпов≥дними табличними значенн€ми. «а результатами такого пор≥вн€нн€ робитьс€ висновок про адекватн≥сть модел≥ ≥ величину ймов≥рност≥, з €кою модель може бути застосована дл€ прийн€тт€ управл≥нських р≥шень.
–озгл€немо детальн≥ше пор€док застосуванн€ парноњ л≥н≥йноњ та найб≥льш попул€рних нел≥н≥йних залежностей
ћодель л≥н≥йноњ регрес≥њ (л≥н≥йне р≥вн€нн€) Ї найпоширен≥шим видом залежност≥ м≥ж економ≥чними зм≥нними.
—користаймос€ методом найменших квадрат≥в, суть €кого пол€гаЇ у наступному: сума квадрат≥в в≥дхилень ординат точки, що спостер≥гаЇтьс€ (Xi, Yi) в≥д в≥дпов≥дноњ ординати точки, що належить регрес≥йн≥й пр€м≥й, повинна бути найменшою

¬икористанн€ 1ћЌ дл€ оц≥нки теоретичних параметр≥в модел≥ парноњ регрес≥њ приводить до таких систем нормальних р≥вн€нь:
a) л≥н≥йна залежн≥сть Y = a0 + a1X.

ѕобудоване л≥н≥йне р≥вн€нн€ може слугувати початковою точкою в раз≥ складних (суттЇво нел≥н≥йних) залежностей.
Ќел≥н≥йн≥ зв'€зки, €к правило, певними перетворенн€ми (зам≥ною зм≥нних чи логарифмуванн€м) звод€ть до л≥н≥йного вигл€ду або апроксимують (наближують) л≥н≥йними функц≥€ми.
б) г≥пербол≥чна залежн≥сть  . «ам≥нюЇмо
. «ам≥нюЇмо  ≥ отримаЇмо л≥н≥йну модель Y = a0 + a1х′.
≥ отримаЇмо л≥н≥йну модель Y = a0 + a1х′.
ƒл€ оц≥нки теоретичних параметр≥в модел≥ складаЇмо систему нормальних р≥вн€нь:

в) парабол≥чна залежн≥сть Y = a0 + a1х2. «ам≥нюЇмо х2 = х′ ≥ отримаЇмо л≥н≥йну модель Y = a0 + a1х′.
ƒл€ оц≥нки теоретичних параметр≥в модел≥ складаЇмо систему нормальних р≥вн€нь:

г) степенева залежн≥сть 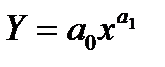 .
.
ЋогарифмуЇмо функц≥ю lnY = ln a0 + a1 · ln ’.
«ам≥нюЇмо логарифми lnY = Y′, ln ’ = ’′, ln a0 = a′.
ќдержуЇмо л≥н≥йну модель Y′ = a′+ a1 · ’′.
—кладаЇмо систему нормальних р≥вн€нь:

 д) експоненц≥альна.
д) експоненц≥альна.
ƒл€ оц≥нки теоретичних параметр≥в зводимо модель до л≥н≥йного вигл€ду:

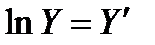 ЋогарифмуЇмо функц≥ю
ЋогарифмуЇмо функц≥ю
 «ам≥нюЇмо логарифм
«ам≥нюЇмо логарифм
ќдержуЇмо л≥н≥йну модель
е) проста модиф≥кована експоненц≥альна 
ћетодом зам≥ни зводимо модель до л≥н≥йного вигл€ду:
|
|
|

ћоделюванн€ зд≥йснюЇтьс€ на основ≥ виб≥рки статистичних даних, €ку студент отримуЇ з в≥дпов≥дних таблиць.
Ћабораторн≥ роботи є 1, 2, 3, 4, 5 студент виконуЇ зг≥дно з завданн€м та вар≥антом вих≥дних даних, €кий отримуЇ у викладача.
ƒќƒј“ ќ¬ќ
ƒл€ спрощенн€ пром≥жних розрахунк≥в використаЇмо вбудовану в електронн≥ таблиц≥ Microsoft Excel статистичну функц≥ю Ћ»Ќ≈…Ќ. ÷€ функц≥€ застосовуЇ метод найменших квадрат≥в, щоб визначити оц≥нки параметр≥вл≥н≥йноњ регрес≥њ.
Ћ»Ќ≈…Ќ (в≥дом≥_значенн€_Y; в≥дом≥_значенн€_’; конст; статистика).
–езультат Ц це оц≥нка параметр≥в л≥н≥йноњ регрес≥њ та регрес≥йна статистика.
ƒл€ цього треба:
1) в≥дм≥тити поле, де буде знаходитись результат розм≥ром (k + 1) ´ 5, або m1 ´ 5; m1 = k + 1
2) ув≥йти у "майстер функц≥й f ". ” категор≥€х вибираЇмо "статистична", а в функц≥€х Ц Ћ»Ќ≈…Ќ. ¬водимо адреси значень Y, ’ та значенн€ константи ≥ статистики;
3) дл€ того, щоб отримати на екран≥ результат, натискаЇмо спершу клав≥шу F2, а пот≥м Ctrl+Shift+≈nter.
‘ункц≥€ може додатково обчислювати регрес≥йну статистику (рис.1.1).
Ђ¬≥дом≥ значенн€ Yї Ч множина значень Y. якщо масив Y маЇ один стовпець, то кожний стовпець масиву Ђв≥дом≥_значенн€_’ї ≥нтерпретуютьс€ €к окрема зм≥нна. якщо масив Ђв≥дом≥_значенн€_Yї маЇ один р€док, то кожний р€док Ђв≥домих значень ’ї ≥нтерпретуЇтьс€ €к окрема зм≥нна.
Ђ¬≥дом≥_значенн€_’ї Ч множина значень ’, що враховуЇ або одну (парна регрес≥€), або к≥лька зм≥нних (множинна регрес≥€). якщо Ђв≥дом≥_значенн€_’ї пропустили, то вважаЇтьс€, що це масив {1; 2; 3;...} такого самого розм≥ру, €к n Ђв≥домих_значень Yї.
Ђ онстї Ч лог≥чне значенн€.
якщо Ђконстї маЇ значенн€ Ђложьї, то a 0 беруть таким, що дор≥внюЇ нулю: значенн€ aдобирають так, щоб виконувалас€ р≥вн≥сть Y = ’ј (модель без в≥льного члена).
якщо Ђконстї маЇ значенн€ Ђистинаї, то a 0 обчислюЇтьс€ традиц≥йно (модель з в≥льним членом).
Ђ—татистикаї Ч лог≥чне значенн€, €ке вказуЇ, чи потр≥бно обчислювати додаткову статистику за регрес≥Їю.
якщо Ђстатистикаї маЇ значенн€ Ђистинаї, то функц≥€ Ћ»Ќ≈…Ќ обчислюЇ додаткову регрес≥йну статистику у вигл€д≥ масиву (див. рис. 1.1).

| 
| Е | 
| 
|

| 
| Е | 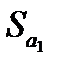
| 
|
| R2 | 
| |||
| F | —туп≥нь свободи nЦm | |||

| 
|
–ис. 1.1. —татистика функц≥њ Ћ»Ќ≈…Ќ
де  Ц оц≥нка параметра
Ц оц≥нка параметра  , j=1..k;
, j=1..k;
 Ц оц≥нка в≥льного члена регрес≥њ;
Ц оц≥нка в≥льного члена регрес≥њ;
 Ц стандартна похибка оц≥нки параметра a≥;
Ц стандартна похибка оц≥нки параметра a≥;
R2 Ц коеф≥ц≥Їнт детерм≥нац≥њ;
 Ц стандартна похибка залишк≥в;
Ц стандартна похибка залишк≥в;
F Ц F-критер≥й.
 Ц середнЇ значенн€ Yфакт.
Ц середнЇ значенн€ Yфакт.
—туп≥нь свободи дор≥внюЇ (n Ц m), де n Ц к≥льк≥сть спостере≠жень, m Ц к≥льк≥сть зм≥нних у модел≥; це значенн€ необх≥дне дл€ визначенн€ табличного значенн€ F-критер≥ю.
 Цсума квадрат≥в в≥дхиленн€, що по€снюЇтьс€ регрес≥Їю;
Цсума квадрат≥в в≥дхиленн€, що по€снюЇтьс€ регрес≥Їю;
 Ц сума квадрат≥в в≥дхиленн€, що по€снюЇтьс€ похибкою u.
Ц сума квадрат≥в в≥дхиленн€, що по€снюЇтьс€ похибкою u.
якщо статистика маЇ значенн€ Ђложьї чи њњ пропустили, то функц≥€ Ћ»Ќ≈…Ќ обчислюЇ лише коеф≥ц≥Їнти aj та константу a0.
Ћабораторна робота є 1. ЂЋ≥н≥йна модельї
«г≥дно з виб≥ркою статистичних даних побудувати л≥н≥йну модель залежност≥ Y в≥д X виду:  .
.
ћета роботи:
визначити анал≥тичну залежн≥сть м≥ж досл≥дними даними ≥з застосуванн€м методу найменших квадрат≥в (знайти параметри модел≥);
представити модель на граф≥ку (граф≥чне в≥дображенн€ модел≥ засновуЇтьс€ на побудов≥ л≥н≥њ тренду в пр€мокутних координатах Y-X).
|
|
|
¬их≥дн≥ дан≥ дл€ розрахунку моделей лабораторноњ роботи є 1
| ¬ар≥ант 1 | ¬ар≥ант 2 | ¬ар≥ант 3 | ¬ар≥ант 4 | ¬ар≥ант 5 | |||||||||
| Y | ’ | Y | ’ | Y | ’ | Y | ’ | Y | ’ | ||||
| 12,3 | 9,6 | 16,1 | 12,2 | 12,7 | 12,4 | 15,8 | 12,3 | 16,9 | 19,3 | ||||
| 14,7 | 8,1 | 16,3 | 12,9 | 10,3 | 19,4 | 17,7 | 18,7 | ||||||
| 15,8 | 6,3 | 17,8 | 8,1 | 13,3 | 10,1 | 20,3 | 6,1 | 18,3 | 8,9 | ||||
| 16,3 | 5,5 | 17,6 | 14,7 | 8,4 | 27,8 | 6,2 | 18,4 | 6,3 | |||||
| 17,1 | 4,1 | 18,5 | 7,6 | 16,9 | 6,3 | 29,3 | 5,1 | 19,7 | |||||
| 20,9 | 2,8 | 18,9 | 7,4 | 20,1 | 6,2 | 24,4 | 4,3 | 20,8 | 5,5 | ||||
| 21,4 | 1,6 | 20,1 | 6,1 | 23,4 | 5,4 | 31,3 | 3,8 | 21,3 | |||||
| 22,8 | 0,9 | 24,3 | 5,3 | 24,5 | 5,3 | 32,8 | 22,9 | 2,9 | |||||
| 23,9 | 0,8 | 25,8 | 2,7 | 28,4 | 32,9 | 2,7 | 25,4 | 1,3 | |||||
| 24,1 | 0,4 | 26,7 | 2,6 | 30,7 | 4,8 | 34,7 | 2,5 | 26,9 | 0,7 | ||||
| ¬ар≥ант 6 | ¬ар≥ант 7 | ¬ар≥ант 8 | ¬ар≥ант 9 | ¬ар≥ант 10 | |||||||||
| Y | ’ | Y | ’ | Y | ’ | Y | ’ | Y | ’ | ||||
| 10,9 | 12,4 | 16,3 | 10,3 | 16,7 | 15,1 | 15,9 | 6,3 | 12,8 | 6,3 | ||||
| 11,3 | 10,1 | 16,7 | 8,1 | 17,3 | 16,1 | 12,9 | 5,1 | ||||||
| 12,8 | 8,4 | 18,1 | 6,4 | 18,4 | 12,4 | 17,4 | 6,1 | 13,1 | |||||
| 13,8 | 18,9 | 19,5 | 9,3 | 18,3 | 5,5 | 14,4 | 4,2 | ||||||
| 14,9 | 7,9 | 19,3 | 4,1 | 20,3 | 8,6 | 18,9 | 15,8 | 3,3 | |||||
| 15,6 | 5,4 | 20,4 | 3,3 | 21,4 | 5,1 | 20,4 | 4,3 | 16,3 | 2,1 | ||||
| 18,1 | 6,1 | 21,5 | 3,3 | 25,5 | 3,3 | 21,3 | 17,9 | ||||||
| 19,4 | 3,1 | 24,6 | 2,7 | 26,9 | 3,2 | 22,8 | 18,1 | 1,9 | |||||
| 27,8 | 2,1 | 27,8 | 23,4 | 3,5 | 19,3 | 1,7 | |||||||
| 21,3 | 2,1 | 27,9 | 0,9 | 30,1 | 2,1 | 25,7 | 3,1 | 20,4 | 1,1 | ||||
| ¬ар≥ант 11 | ¬ар≥ант 12 | ¬ар≥ант 13 | ¬ар≥ант 14 | ¬ар≥ант 15 | |||||||||
| Y | ’ | Y | ’ | Y | ’ | Y | ’ | Y | ’ | ||||
| 10,4 | 12,7 | 10,7 | 9,1 | 15,6 | 12,3 | 12,3 | 12,3 | 12,3 | 6,3 | ||||
| 11,5 | 11,8 | 11,8 | 8,6 | 15,8 | 10,1 | 12,5 | 10,1 | 12,9 | |||||
| 12,7 | 10,3 | 13,8 | 8,6 | 16,3 | 8,7 | 13,7 | 8,8 | 13,4 | |||||
| 13,8 | 9,1 | 14,9 | 16,9 | 6,5 | 13,9 | 7,3 | 14,7 | 5,8 | |||||
| 14,3 | 15,1 | 7,4 | 20,1 | 3,1 | 14,7 | 6,9 | 15,1 | 5,3 | |||||
| 14,9 | 8,5 | 16,3 | 7,1 | 21,3 | 15,1 | 5,1 | 16,9 | 5,1 | |||||
| 15,1 | 7,4 | 17,1 | 6,9 | 24,9 | 2,1 | 16,3 | 17,3 | ||||||
| 16,3 | 18,7 | 6,2 | 25,8 | 1,5 | 17,4 | 4,1 | 18,7 | 4,1 | |||||
| 17,9 | 6,3 | 18,9 | 5,3 | 26,9 | 1,4 | 18,1 | 3,2 | 19,8 | 3,2 | ||||
| 18,4 | 5,1 | 19,3 | 4,2 | 27,3 | 0,9 | 18,9 | 3,1 | 20,1 | 2,7 | ||||
| ¬ар≥ант 16 | ¬ар≥ант 17 | ¬ар≥ант 18 | ¬ар≥ант 19 | ¬ар≥ант 20 | |||||||||
| Y | ’ | Y | ’ | Y | ’ | Y | ’ | Y | ’ | ||||
| 10,3 | 6,7 | 15,1 | 10,7 | 12,7 | 20,8 | 5,1 | 6,9 | 10,1 | |||||
| 10,9 | 6,5 | 8,1 | 12,8 | 9,1 | 21,9 | 10,3 | 9,4 | ||||||
| 11,7 | 15,6 | 8,7 | 21,9 | 4,9 | 12,5 | 6,5 | |||||||
| 12,8 | 5,9 | 15,9 | 6,7 | 13,9 | 8,8 | 23,4 | 4,9 | 12,4 | 5,1 | ||||
| 13,9 | 4,1 | 16,1 | 6,6 | 14,1 | 8,6 | 25,7 | 3,1 | 13,7 | |||||
| 14,7 | 16,3 | 15,8 | 7,1 | 26,8 | 16,8 | 4,2 | |||||||
| 15,1 | 3,8 | 17,8 | 6,5 | 16,1 | 6,3 | 27,1 | 2,8 | 19,3 | 3,1 | ||||
| 16,9 | 2,7 | 17,3 | 5,1 | 28,1 | 2,1 | 20,1 | 2,8 | ||||||
| 21,9 | 1,9 | 5,1 | 18,9 | 4,2 | 30,3 | 1,8 | 21,7 | ||||||
| 18,7 | 0,8 | 18,4 | 4,3 | 18,9 | 2,8 | 31,4 | 0,9 | 25,8 | 1,9 | ||||
| ¬ар≥ант 21 | ¬ар≥ант 22 | ¬ар≥ант 23 | ¬ар≥ант 24 | ¬ар≥ант 25 | |||||||||
| Y | ’ | Y | ’ | Y | ’ | Y | ’ | Y | ’ | ||||
| 19,8 | 10,5 | 5,6 | 7,9 | 15,6 | 9,1 | 10,7 | 6,1 | 10,1 | 6,7 | ||||
| 20,3 | 9,4 | 5,6 | 7,8 | 15,8 | 5,1 | ||||||||
| 21,4 | 8,3 | 5,8 | 7,6 | 16,1 | 7,1 | 10,9 | 10,7 | 6,9 | |||||
| 22,9 | 6,1 | 5,9 | 6,1 | 18,4 | 11,5 | 6,3 | 11,3 | 6,9 | |||||
| 24,6 | 5,4 | 6,7 | 6,8 | 11,9 | 5,8 | 11,8 | 5,4 | ||||||
| 27,8 | 2,2 | 7,9 | 5,8 | 19,1 | 6,3 | 5,7 | 12,4 | 7,1 | |||||
| 29,3 | 8,3 | 5,5 | 20,3 | 6,3 | 15,7 | 6,3 | |||||||
| 30,1 | 1,9 | 8,7 | 5,4 | 21,7 | 13,7 | 5,4 | 15,8 | 6,5 | |||||
| 33,4 | 0,7 | 10,1 | 4,1 | 29,8 | 6,1 | 14,1 | 5,1 | 16,1 | 6,1 | ||||
| 35,8 | 0,6 | 15,4 | 30,3 | 5,8 | 14,8 | 5,8 | |||||||
Ћабораторна робота є 2. Ђ—тепенева функц≥€ї
|
|
|
«г≥дно з виб≥ркою статистичних даних побудувати степеневу модель залежност≥ Y в≥д X виду:  .
.
ћета роботи:
визначити анал≥тичну залежн≥сть м≥ж досл≥дними даними ≥з застосуванн€м методу найменших квадрат≥в (знайти параметри модел≥);
представити модель на граф≥ку (граф≥чне в≥дображенн€ модел≥ засновуЇтьс€ на побудов≥ л≥н≥њ тренду в пр€мокутних координатах Y-X).
¬их≥дн≥ дан≥ дл€ розрахунку моделей лабораторноњ роботи є 2
| ¬ар≥ант 1 | ¬ар≥ант 2 | ¬ар≥ант 3 | ¬ар≥ант 4 | ¬ар≥ант 5 | ¬ар≥ант 6 | |||||||||||
| Y | X | Y | X | Y | X | Y | X | Y | X | Y | X | |||||
| 30,4 | 50,5 | 19,3 | 20,5 | 80,5 | 30,5 | 20,1 | 30,1 | 50,3 | 60,1 | 80,3 | ||||||
| 31,5 | 50,7 | 19,5 | 20,7 | 80,4 | 20,4 | 30,3 | 49,8 | 60,2 | 80,4 | |||||||
| 31,6 | 50,8 | 19,8 | 21,3 | 80,3 | 27,7 | 21,9 | 30,4 | 48,7 | 81,7 | |||||||
| 39,7 | 59,3 | 19,9 | 22,4 | 68,1 | 80,1 | 27,6 | 28,8 | 30,5 | 45,5 | 60,1 | 82,8 | |||||
| 38,8 | 60,1 | 22,7 | 68,2 | 78,9 | 27,6 | 29,5 | 30,7 | 60,3 | 82,9 | |||||||
| 40,5 | 70,3 | 68,3 | 78,5 | 29,6 | 31,8 | 42,1 | 60,4 | 85,1 | ||||||||
| 42,7 | 23,1 | 29,1 | 68,4 | 78,2 | 25,5 | 29,8 | 32,1 | 40,3 | 60,5 | 87,1 | ||||||
| 49,9 | 75,5 | 24,7 | 30,3 | 68,5 | 78,1 | 21,6 | 30,4 | 33,4 | 38,4 | 61,6 | 88,3 | |||||
| 50,1 | 76,6 | 28,4 | 31,4 | 68,6 | 21,3 | 30,7 | 35,5 | 35,3 | 62,7 | 89,4 | ||||||
| 50,2 | 77,8 | 29,3 | 68,7 | 76,7 | 21,3 | 30,9 | 36,6 | 30,3 | 63,8 | 90,5 | ||||||
| 53,3 | 79,8 | 29,5 | 68,8 | 75,6 | 21,1 | 35,4 | 30,1 | 64,7 | 91,6 | |||||||
| 55,7 | 79,9 | 29,9 | 34,1 | 68,8 | 74,4 | 20,9 | 37,1 | 28,8 | 28,3 | 65,5 | ||||||
| 60,1 | 30,1 | 35,6 | 68,9 | 73,1 | 20,2 | 39,5 | 29,9 | 27,6 | 66,7 | 92,3 | ||||||
| 75,5 | 31,3 | 37,8 | 69,9 | 72,8 | 20,1 | 40,2 | 20,1 | 25,5 | 68,1 | 93,7 | ||||||
| 81,3 | 93,3 | 32,4 | 39,5 | 70,1 | 70,7 | 19,9 | 46,8 | 20,2 | 69,7 | 94,5 | ||||||
| ¬ар≥ант 7 | ¬ар≥ант 8 | ¬ар≥ант 9 | ¬ар≥ант 10 | ¬ар≥ант 11 | ¬ар≥ант 12 | |||||||||||
| Y | X | Y | X | Y | X | Y | X | Y | X | Y | X | |||||
| 82,3 | 99,9 | 19,1 | 20,5 | 44,1 | 50,5 | 30,5 | 46,6 | 65,5 | 70,6 | 59,1 | ||||||
| 82,5 | 98,7 | 19,2 | 20,7 | 50,6 | 40,5 | 70,7 | 48,8 | |||||||||
| 88,6 | 97,6 | 19,3 | 21,3 | 43,9 | 50,7 | 27,7 | 39,1 | 70,8 | 47,7 | 55,7 | ||||||
| 96,6 | 22,7 | 43,8 | 50,8 | 27,6 | 37,1 | 61,8 | 70,9 | 44,3 | ||||||||
| 95,5 | 20,1 | 22,4 | 43,7 | 51,1 | 35,5 | 62,1 | 72,3 | 42,7 | 50,2 | |||||||
| 22,5 | 43,6 | 52,2 | 26,6 | 30,9 | 57,8 | 72,4 | 41,7 | 50,1 | ||||||||
| 89,4 | 21,1 | 53,4 | 25,5 | 30,7 | 55,2 | 72,5 | 39,3 | 49,3 | ||||||||
| 89,5 | 93,5 | 25,1 | 41,1 | 55,5 | 22,4 | 30,1 | 43,9 | 72,9 | 38,8 | 48,1 | ||||||
| 89,7 | 93,1 | 24,1 | 21,6 | 29,7 | 42,5 | 80,1 | 30,7 | 47,7 | ||||||||
| 90,1 | 25,6 | 21,5 | 29,4 | 85,5 | 29,3 | 46,7 | ||||||||||
| 90,2 | 27,1 | 60,1 | 21,3 | 29,3 | 38,8 | 29,1 | 44,5 | |||||||||
| 90,3 | 24,4 | 27,9 | 39,8 | 20,1 | 28,8 | 35,9 | 88,1 | 28,3 | 41,3 | |||||||
| 92,1 | 90,3 | 25,5 | 28,1 | 39,7 | 20,1 | 21,7 | 32,4 | 89,3 | 27,4 | 30,9 | ||||||
| 92,3 | 90,1 | 26,1 | 29,3 | 39,6 | 65,5 | 20,5 | 31,2 | 90,1 | 26,5 | 30,8 | ||||||
| 93,3 | 27,3 | 29,5 | 39,6 | 66,6 | 19,7 | 20,3 | 30,7 | 90,2 | 25,5 | 30,7 | ||||||
| ¬ар≥ант 13 | ¬ар≥ант 14 | ¬ар≥ант 15 | ¬ар≥ант 16 | ¬ар≥ант 17 | ¬ар≥ант 18 | |||||||||||
| Y | X | Y | X | Y | X | Y | X | Y | X | Y | X | |||||
| 50,3 | 61,7 | 30,1 | 40,1 | 39,7 | 30,4 | 64,3 | ||||||||||
| 50,7 | 60,3 | 81,7 | 24,1 | 50,1 | 29,4 | 42,3 | 28,8 | 41,6 | 35,5 | 68,7 | ||||||
| 45,1 | 51,3 | 89,1 | 24,1 | 48,9 | 31,3 | 44,1 | 31,3 | 42,4 | 37,8 | 70,1 | ||||||
| 45,2 | 61,8 | 89,4 | 24,3 | 45,8 | 32,4 | 43,5 | 38,9 | 75,5 | ||||||||
| 45,4 | 55,1 | 60,1 | 80,5 | 24,5 | 45,5 | 28,3 | 49,7 | 27,9 | 46,6 | 40,1 | ||||||
| 45,5 | 56,3 | 59,8 | 80,3 | 24,7 | 40,5 | 27,8 | 50,3 | 26,3 | 47,7 | 47,7 | 80,3 | |||||
| 45,5 | 57,1 | 62,3 | 90,1 | 24,8 | 39,9 | 32,7 | 55,8 | 33,7 | 48,9 | 48,9 | 81,8 | |||||
| 58,3 | 63,4 | 90,3 | 24,9 | 39,1 | 33,8 | 56,9 | 35,8 | 50,1 | 49,9 | 82,9 | ||||||
| 46,1 | 63,9 | 91,7 | 25,1 | 34,7 | 60,3 | 39,6 | 52,3 | 50,1 | ||||||||
| 46,7 | 59,1 | 64,5 | 91,9 | 25,3 | 35,9 | 61,9 | 52,3 | 85,1 | ||||||||
| 47,1 | 59,3 | 65,6 | 25,6 | 38,1 | 68,8 | 41,2 | 57,9 | 86,9 | ||||||||
| 47,8 | 60,3 | 66,7 | 96,1 | 25,7 | 33,1 | 44,1 | 70,4 | 42,3 | 60,1 | 55,6 | 90,3 | |||||
| 47,9 | 61,7 | 67,8 | 97,1 | 25,8 | 31,3 | 45,3 | 71,7 | 43,3 | 64,3 | 57,8 | 91,4 | |||||
| 48,1 | 68,8 | 97,8 | 48,8 | 78,8 | 45,6 | 65,9 | 59,3 | 92,2 | ||||||||
| 69,9 | 99,1 | 30,9 | 49,1 | 79,3 | 47,8 | 66,7 | 60,1 | 93,3 | ||||||||
| ¬ар≥ант 19 | ¬ар≥ант 20 | ¬ар≥ант 21 | ¬ар≥ант 22 | ¬ар≥ант 23 | ¬ар≥ант 24 | |||||||||||
| Y | X | Y | X | Y | X | Y | X | Y | X | Y | X | |||||
| 40,3 | 67,1 | 26,3 | 59,6 | 30,1 | 50,5 | 19,1 | 20,2 | 35,1 | 22,6 | 25,1 | 25,2 | |||||
| 45,7 | 70,4 | 27,8 | 60,3 | 31,2 | 50,7 | 19,4 | 20,7 | 34,5 | 22,9 | 25,2 | 25,5 | |||||
| 46,8 | 80,1 | 65,6 | 31,3 | 50,8 | 19,8 | 21,5 | 34,9 | 23,1 | 28,8 | 27,6 | ||||||
| 47,9 | 85,5 | 30,1 | 66,8 | 39,1 | 59,2 | 19,9 | 22,4 | 34,9 | 26,5 | 29,9 | 28,9 | |||||
| 48,8 | 86,6 | 31,2 | 70,1 | 38,5 | 60,1 | 21,9 | 22,7 | 36,8 | 27,7 | 30,1 | ||||||
| 49,4 | 86,7 | 33,4 | 40,1 | 70,5 | 22,7 | 37,7 | 29,4 | 30,4 | 30,8 | |||||||
| 50,1 | 76,3 | 42,8 | 23,1 | 29,1 | 38,2 | 29,5 | 30,5 | 35,3 | ||||||||
| 50,9 | 89,1 | 77,9 | 49,9 | 75,5 | 24,6 | 30,3 | 44,3 | 30,8 | 30,6 | 38,4 | ||||||
| 60,3 | 90,3 | 37,1 | 78,4 | 50,1 | 76,5 | 27,4 | 31,4 | 48,1 | 31,1 | 30,7 | 40,3 | |||||
| 65,3 | 91,4 | 38,4 | 79,3 | 50,2 | 77,7 | 28,3 | 32,4 | 51,5 | 31,2 | 30,9 | 42,7 | |||||
| 66,4 | 92,5 | 39,1 | 80,1 | 53,3 | 79,8 | 29,5 | 33,5 | 52,5 | 31,6 | 31,8 | ||||||
| 69,5 | 93,6 | 40,5 | 81,5 | 55,1 | 79,9 | 29,9 | 34,2 | 52,3 | 31,8 | 32,1 | 45,5 | |||||
| 70,5 | 94,7 | 46,6 | 86,6 | 60,1 | 30,1 | 35,6 | 52,5 | 33,4 | 48,7 | |||||||
| 70,9 | 98,1 | 47,8 | 90,4 | 75,3 | 31,3 | 37,8 | 53,6 | 34,4 | 35,5 | 49,8 | ||||||
| 98,2 | 50,1 | 95,6 | 81,3 | 93,5 | 32,4 | 55,8 | 35,4 | 36,6 | ||||||||
| ¬ар≥ант 25 | ||||||||||||||||
| Y | X | |||||||||||||||
| 81,3 | 93,3 | |||||||||||||||
| 75,5 | ||||||||||||||||
| 60,1 | ||||||||||||||||
| 55,7 | 79,9 | |||||||||||||||
| 53,3 | 79,8 | |||||||||||||||
| 50,2 | 77,8 | |||||||||||||||
| 50,1 | 76,6 | |||||||||||||||
| 49,9 | 75,5 | |||||||||||||||
| 42,7 | ||||||||||||||||
| 40,5 | 70,3 | |||||||||||||||
| 39,7 | 59,3 | |||||||||||||||
| 38,8 | 60,1 | |||||||||||||||
| 31,6 | 50,8 | |||||||||||||||
| 31,5 | 50,7 | |||||||||||||||
| 30,4 | 50,5 |
Ћабораторна робота є 3. Ђѕарабол≥чна функц≥€ї
|
|
|
|
|
|
«г≥дно з виб≥ркою статистичних даних побудувати парабол≥чнумодель залежност≥ Y в≥д X виду:  .
.
ћета роботи:
визначити анал≥тичну залежн≥сть м≥ж досл≥дними даними ≥з застосуванн€м методу найменших квадрат≥в (знайти параметри модел≥);
представити модель на граф≥ку (граф≥чне в≥дображенн€ модел≥ засновуЇтьс€ на побудов≥ л≥н≥њ тренду в пр€мокутних координатах Y-X).
¬их≥дн≥ дан≥ дл€ розрахунку моделей лабораторноњ роботи є 3
| ¬ар≥ант 1 | ¬ар≥ант 2 | ¬ар≥ант 3 | ¬ар≥ант 4 | ¬ар≥ант 5 | |||||||||
| Y | X | Y | X | Y | X | Y | X | Y | X | ||||
| 27,75 | 86,82 | 14,30 | 28,77 | ||||||||||
| 28,37 | 85,42 | 15,15 | 28,60 | ||||||||||
| 34,45 | 81,45 | 16,63 | 34,50 | ||||||||||
| 41,32 | 18,87 | 41,57 | |||||||||||
| 48,50 | 33,4 | 21,42 | 49,10 | ||||||||||
| 52,45 | 23,82 | 52,87 | |||||||||||
| 55,55 | 42,80 | 27,67 | 56,20 | ||||||||||
| 62,25 | 46,45 | 29,45 | 62,35 | ||||||||||
| 73,01 | 58,32 | 46,32 | 32,27 | 73,76 | |||||||||
| 76,42 | 71,32 | 38,25 | 36,07 | 76,60 | |||||||||
| 86,32 | 85,31 | 36,3 | 44,20 | 87,64 | |||||||||
| 88,45 | 94,25 | 32,55 | 47,57 | 88,45 | |||||||||
| 95,50 | 97,85 | 26,65 | 50,58 | 96,43 | |||||||||
| 104,00 | 101,85 | 19,87 | 57,30 | 104,07 | |||||||||
| 113,42 | 110,00 | 15,22 | 67,37 | 113,43 | |||||||||
| ¬ар≥ант 6 | ¬ар≥ант 7 | ¬ар≥ант 8 | ¬ар≥ант 9 | ¬ар≥ант 10 | |||||||||
| Y | X | Y | X | Y | X | Y | X | Y | X | ||||
| 15,23 | 7,78 | 26,54 | 19,15 | ||||||||||
| 15,22 | 7,17 | 27,05 | 19,88 | ||||||||||
| 16,64 | 17,30 | 33,08 | 20,88 | ||||||||||
| 19,59 | 19,70 | 39,10 | 22,82 | ||||||||||
| 21,59 | 20,90 | 46,10 | 25,57 | ||||||||||
| 24,82 | 24,42 | 49,10 | |||||||||||
| 27,77 | 24,67 | 52,10 | 31,9 | ||||||||||
| 31,00 | 26,35 | 58,10 | 33,77 | ||||||||||
| 32,37 | 26,60 | 68,12 | 35,8 | ||||||||||
| 36,17 | 27,07 | 71,12 | 39,87 | ||||||||||
| 44,38 | 27,90 | 80,12 | 47,17 | ||||||||||
| 47,64 | 28,39 | 82,13 | 50,57 | ||||||||||
| 52,11 | 30,28 | 89,13 | 54,22 | ||||||||||
| 57,57 | 30,8 | 97,15 | 60,22 | ||||||||||
| 68,10 | 34,8 | 106,19 | 70,4 |
Ћабораторна робота є 4. Ђ√≥пербол≥чна функц≥€ї
«г≥дно з виб≥ркою статистичних даних побудувати г≥пербол≥чнумодель залежност≥ Y в≥д X виду: 
ћета роботи:
визначити анал≥тичну залежн≥сть м≥ж досл≥дними даними ≥з застосуванн€м методу найменших квадрат≥в (знайти параметри модел≥);
представити модель на граф≥ку (граф≥чне в≥дображенн€ модел≥ засновуЇтьс€ на побудов≥ л≥н≥њ тренду в пр€мокутних координатах Y-X).
¬их≥дн≥ дан≥ дл€ розрахунку моделей лабораторноњ роботи є 4
| ¬ар≥ант 1 | ¬ар≥ант 2 | ¬ар≥ант 3 | ¬ар≥ант 4 | ¬ар≥ант 5 | ||||||
| Y | X | Y | X |
ƒата добавлени€: 2015-11-05; ћы поможем в написании ваших работ!; просмотров: 544 | Ќарушение авторских прав ѕоиск на сайте: Ћучшие изречени€: |
√ен: 0.039 с.






