Ошибка репрезентативности (m) показывает, насколько результаты полученные при выборочном исследовании, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования (генеральная совокупность).
Формула ошибки репрезентативности (m) для относительных величин:
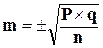или 
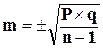, если число наблюдений меньше 30 случаев, где Р – величина показателя, 
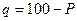, если показатель вычислен на 100, 
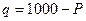, если показатель вычислен на 1000, и т.д., n – число наблюдений.
Например, работающих на предприятии – 1400 человек (n), имеющих кариес зубов – 44 человека. Показатель заболеваемости кариеса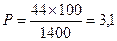 
на 100 работающих, далее вычисляем по формуле
.
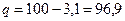
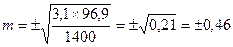Вывод: результаты выборочной совокупности по определению кариеса зубов на предприятии отличаются от генеральной совокупности на ± 0,46 (средняя ошибка ± 0,46).
Формула (m) для средней величины: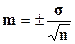 
или 
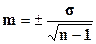, если число наблюдений меньше 30.
Например, у 49 больных (n) гастритом уровень пепсина М=1,0 г%, σ = ±0,35 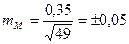г%
г%
Вывод: результаты выборочной совокупности по определению уровня пепсина у 49 больных гастритом отличаются от генеральной совокупности (если бы исследования проводились у всех больных гастритом) на ± 0,05 (средняя ошибка ± 0,05).
Примечание: среднее квадратическое отклонение (σ) характеризует степень рассеивания вариант вокруг средней арифметической (смотри тему №4). Вычисляют по формуле: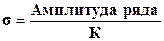 
Амплитуда ряда (см. тему №4)
К – «коэффициент К», (см. приложение №4).
Например, вес 15 детей (n) равен Vmax=45 кг., Vmin=20 кг., отсюда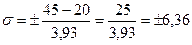 
Вывод: рассеивание средней массы тела у 15 детей составляет ±6,36 кг, т.е. либо в сторону увеличения или уменьшения 6,36 кг.
Доверительные границы (М, P) средних и относительных величин – это границы относительных или средних величин размеров признака выход за пределы которых, вследствие случайных колебаний, имеет незначительную вероятность.
Доверительные границы для средней величины Мген.=Мвыб.± tm, где Мген., выб. – доверительные границы средней величины генеральной и выборочной совокупности, t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже), m – ошибка репрезентативности.
Доверительные границы для относительной величины Pген.=Pвыб.± tm, где Pген., выб. – доверительные границы относительной величины генеральной и выборочной совокупности, t – доверительный критерий (устанавливается исследователем, но должен быть не меньше 2, смотри ниже), m – ошибка репрезентативности.
Предельная ошибка (Δ - дельта) – это максимальная средняя ошибка показателя (m) вычисляется по формуле Δ = tm ( максимально возможная погрешность оценки генеральной совокупности ).
Вероятность безошибочного прогноза (p) – это вероятность, с которой можно утверждать, что в генеральной совокупности относительных или средних величин (P, M) показатели будут находиться в пределах ±tm. Для медицинских исследований степень вероятности безошибочного прогноза (p) должна быть не менее 95%, т.е отображать объективную реальность проведенных исследований на 95%, тогда t=2 (см. ниже).
Зависимость доверительного критерия от степени вероятности безошибочного прогноза p (при n >30)
Таблица 5.1
| Степень вероятности (p) | Доверительный критерий (t) |
| 95,0% | |
| 99,0% | |
| <95% |
Например, определить доверительные границы среднего уровня пепсина при М=1,0 г% у 49 больных гастритом при вероятности безошибочного прогноза равному 95%
n=49, p=95% (t=2), М=1,0 г%, m=±0,05%
Доверительные границы Мген.= Мвыб.± tm, отсюда Мген =1+2×0,05
не более 1 г% + 0,1% = 1,1 г%
М
не менее 1 г% – 0,1 г% = 0,9%
Вывод: установлено с вероятностью безошибочного прогноза 95% средний уровень пепсина в генеральной совокупности у больных гастритом не превышает 1,1 г% и не ниже 0,9 г%.
При сопоставлении двух сравниваемых величин необходимо не только определить их разность, но и оценить достоверность, т.е. достоверно или случайно их различие.
