За стандарт смертности, заболеваемости и так далее принимается какая-либо группа населения. Число умерших или заболевших делят на соответствующие возрастные показатели смертности или заболеваемости, принятого за стандарт населения. Полученные ожидаемые числа населения соответствующих возрастов суммируются и делятся на фактическую численность населения, принятого за стандарт. Частное от этого деления указывает во сколько раз смертность или заболеваемость выше или ниже смертности или заболеваемости населения, принятого за стандарт, и дает возможность вычислить стандартизованный показатель.
Пример вычисления стандартизованных показателей прямым методом (табл. 6.1).
1 этап – вычисление частных и общих простых показателей заболеваемости детей путем определения интенсивных показателей.
Таблица 6.1
Зависимости заболеваемости детей от посещаемости дошкольных учреждений
| Возраст, лет | Посещающие | Не посещающие | ||||
| Число детей | Число заболеваний | Заболеваемость в % | Число детей | Число заболеваний | Заболеваемость в % | |
| До 1 | 8,3 | 9,0 | ||||
| 1 - 3 | 12,5 | 12,5 | ||||
| 3 - 7 | 25,0 | 24,0 | ||||
| Всего | 19,1 | 13,3 |
2-й этап – расчет стандарта. За стандарт принят возрастной состав детей обеих групп (табл. 6.2).
Таблица 6.2
Расчет стандарта
| Возраст, лет | Число детей | |
| Абсолютные | % к итогу | |
| До 1 | 60+100=160 | 26,2 |
| 1 - 3 | 80+120=200 | 32,8 |
| 3 - 7 | 200+50=250 | 41,0 |
| Всего | 340+270=610 | 100,0 |
3-й этап – исчисление стандартизованных показателей заболеваемости («ожидаемого» при одинаковом возрастном составе детей) (табл. 6.3).
Таблица 6.3
Расчет стандартизованных показателей
| Возраст | Всего детей | Заболеваемость детей | |||
| посещающих дошкольные учреждения | не посещающих дошкольных учреждений | ||||
| % к итогу | Простой | Стандартизованный | Простой | Стандартизованный | |
| До 1 | 26,2 | 8,3 | 2,2 | 9,0 | 2,4 |
| 1 - 3 | 32,8 | 12,5 | 4,1 | 12,5 | 4,1 |
| 3 - 7 | 41,0 | 25,0 | 10,3 | 24,0 | 9,8 |
| Всего | 100,0 | 19,1 | 16,6 | 13,3 | 16,3 |
Данные граф 2, 3 и 5 переписаны из предыдущих таблиц. Для получения стандартизованного показателя исходят из следующего (графы 4 и 6): если на 100 детей, посещающих дошкольные учреждения, приходится 8,3 заболевших, то, сколько же придется заболевших на соответствующую группу стандарта, то есть на 26,2 (см.табл. 6.2).
Техника вычисления
1. Составление пропорции:
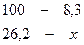
2. Вычисление показателя:
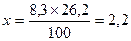и т.д.
Стандартизованные показатели заболеваемости получаются в результате суммирования граф 4 и 6, т.е. соответственно 16,6 и 16,3%.
Оценка стандартизованных показателей: простые показатели заболеваемости были выше в дошкольных учреждениях по сравнению с детьми воспитывающих дома (соответственно 19,1 и 13,3%). Стандартизованные показатели свидетельствуют, что разницы в зависимости почти нет (16,6 и 16,3%). Следовательно, если бы возрастной состав сравниваемых детей был бы одинаковым, то разница в заболеваемости не было бы.
Динамические ряды
Изучение динамических процессов имеет большое значение для правильного анализа социально-медицинских, клинических явлений, прогнозирования и планирования лечебно-профилактических и организационных мероприятий.
Динамическим рядом называется совокупность однородных статистических величин, показывающих изменение какого-либо явления во времени.
Уровнем ряда являются числа, составляющие динамический ряд.
Типы динамических рядов.
Моментный – величины, характеризующие размеры явления в определенные моменты или дату. Например, численность населения КР на конец соответствующего года. Их величины не подлежат делению или суммированию в данный момент.
Интервальный – величины явления за определенный интервал времени. Например, число родившихся по годам. Внутри каждого года величины можно разделить по кварталам, месяца и т.д. Также годовые величины можно суммировать по трех, пятилеткам и т.д.
Динамический ряд может состоять из абсолютных и производных величин (относительных и средних) и соответственно называется простым и сложным.
