Абсолютные величины в медицине дают большую информацию о размере, силе явления или признаков. Например, возраст, рост, вес, величина кровяного давления человека и т.д. Однако во многих случаях абсолютная величина не показывает размер, силу явления или признака. Абсолютные величины являются мало пригодными для сравнения их с другими величинами, характеризующими явления. Они нужны только как промежуточная стадия для получения относительных показателей.
Например, в городе А заболело 2000 человек, а в городе Б – 1500. Это не означает, что в городе А заболевают чаще, чем в городе Б. Для того, чтобы определить размер явления, необходимо учитывать различия в численности населения данных городов, т.е. учесть величину среды (численность населения), в которой происходит явление (число больных). Например, население в городе А равно 8000 человек, а в городе Б – 3000. Отсюда, несмотря на большее число больных в городе А, они составляют около четверти всего населения (2000:8000). А в городе Б при меньшем числе больных они составляют половину населения (1500:3000). Таким образом, во многих случаях сравнивают не абсолютные величины, а так называемые относительные величины.
Относительные величины – это результат сравнения (отношения, деления) двух величин.
Виды относительных величин:
· интенсивные;
· структуры;
· соотношения;
· наглядности.
Интенсивные показатели характеризуют распространение или частоту изучаемого явления или признака в среде. (Например, численность населения в г. Н (или величина среды, в которой происходит явление) – 5000, число больных (или размер явления) – 250). Интенсивный показатель отвечает на вопрос: «как часто явление встречается в среде?».
Методика вычисления:
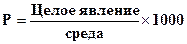
P – интенсивный показатель
Целое явление – количество больных
Среда – численность населения
1. Составление пропорции:
5000 – 250
1000 - х
2. Вычисление показателя:
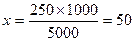 ‰ (или 50 больных на 1000 населения)
‰ (или 50 больных на 1000 населения)
Вывод: в г. Н приходится 50 больных на 1000 населения (50‰)
Величина основания интенсивных показателей
За величину основания обычно выбирают – 100, 1000, 10000, 100000 и т.д. (при вычислении рождаемости, смертности, естественного прироста населения, общие заболеваемости за основание обычно принимают 1000 чел. населения; вычисление размеров смертности или заболеваемости в отношении какой либо отдельной болезни или группы болезней производится на 10 000 или 100 000 населения, вычисления показателей временной нетрудоспособности в связи с заболеваниями производится на 100 работающих). Соответственно, коэффициент интенсивности выражается в процентах – 100 (%), промилле – 1000 (‰), продецимилле – 10000 (‰о), просантимилле – 100000 (‰оо).
Практически основания более 1000 лучше обозначать не математическими знаками (‰о), а цифрами – на 10000, 100000 и т.д. населения.
Показатели структуры:
· экстенсивный;
· координации;
· правдоподобия.
Экстенсивные показатели характеризуют состав или структуру явления, соотношение размеров частей явления к целому (показывает долю или удельный вес). Экстенсивный показатель отвечает на вопрос: «какая часть?». Экстенсивный показатель показывает, как распределяется изучаемое явление на свои составные части, каков удельный вес данного явления по отношению ко всей его величине (отношение части к целому). (Например, число заболеваний (или явление в целом)) – 250, из них больных с заболеванием органов дыхания (или часть целого) – 125.
Методика вычисления:
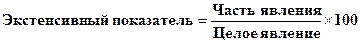
Часть явления – больные с заболеванием органов дыхания
Целое явление – общее количество заболеваний
1. Составление пропорции.
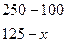
2. Вычисление показателя.
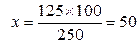 %.
%.
Вывод: из всего количество заболеваний удельный вес больных с заболеванием органов дыхания составляет 50%.
Для вычисления экстенсивного показателя обычно величину основания принимают за 100 и выражают в процентах – 100 (%), но можно принять за 1000, 10000 и т.д. (очень редко).
При вычислении нескольких экстенсивных показателей, сумма всех показателей обязательно должна быть равной 100 (Например, болезни органов дыхания составляют – 50%, инфекционные и паразитарные – 25%, болезни мочеполовой системы – 25%).
Различия между интенсивным и экстенсивным показателями (эти два показателя по своему содержанию значительно отличаются):
| Интенсивный показатель | Экстенсивный показатель |
| 1. Сравнивают между собой | 1. Не сравнивают, или сравнивают с большой осторожностью, глубоко зная сущность сравниваемых явлений |
| 2. Необходимо иметь среду (численность населения) и явление, произошедшее в данной среде (число больных определенным заболеванием). | 2. Надо иметь целое явление (общее число заболеваний) без среды и часть его (число заболеваний определенной нозоологии). |
| 3. С изменением среды изменяется явление | С изменением целого явления его часть может, не изменяться. |
| 4. Явление связано со средой. | Явление не связано со средой. |
| 5. Отвечает на вопрос: «Как часто?» | Отвечает на вопрос: «Какая часть?» |
Примечание: экстенсивный показатель нельзя применять для установления динамики изучаемого явления во времени или для сравнения степени его распространения в двух или нескольких группах населения.
Показатели координации характеризует соотношение частей целого между собой. Например, в городе Н число врачей 200, число средних медицинских работников – 600.
Методика вычисления:
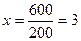
Вывод: соответствие врачей и средних медицинских работников относится как 1:3.
Коэффициенты правдоподобия – это числовые соотношения одноименных показателей структуры, рассчитанные на двух разных совокупностях. В таблице 3.1 в графе 6 приведены коэффициенты правдоподобия, когда показатели структуры г. А делятся на показатели структуры в г. Б.
Таблица 3.1
Расчет коэффициентов правдоподобия заболевания пародонтозом в зависимости от возраста
| Возраст матери (годы) | Коэффициент правдоподобия | ||||
| Город А | Город Б | ||||
| Число случаев | Структуры (в %) | Число случаев | Структура (в %) | ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| До 19 | 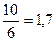
| ||||
| 20-24 | 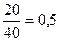
| ||||
| 25-29 | 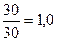
| ||||
| 30-34 | 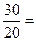 1,5 1,5
| ||||
| 35 и выше | 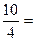 2,5 2,5
| ||||
| Всего | 210 | 100 | 200 | 100 | 1,0 |
Вывод: в городе А по сравнению с городом Б доля заболевания пародонтозом выше в возрастной группе 35 лет и старше (в 2,5 раза) и ниже в возрастной группе 20-24 года (в 0,5 раз). Коэффициент правдоподобия обычно применяется когда нет возможности сравнивать интенсивные показатели (во сколько раз одно явление больше другого).
Показатель соотношения характеризует отношения между разнородными величинами (обеспечение населения больничными койками, врачами, лекарствами). Обычно рассчитывают на 10000. Например, численность населения – 5000, число больничных коек – 250. Рассчитать сколько приходится больничных коек на 10000 населения.
Методика вычисления:
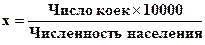
1. Составление пропорции.
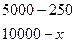
2. Вычисление показателя.
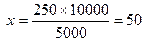 .
.
Вывод: на 10000 населения приходится 50 коек.
Показатель наглядности характеризует отношение каждой из сравниваемых величин к исходному уровню, который принимается за условную величину (обычно за 100).
В таблице 3.2 даны показатели наглядности.
Таблица 3.2
Численность врачей-стоматологов в г. «Н» за 2002-2007 гг.
| Годы | Численность врачей | Показатель наглядности |
Рассчитать показатели наглядности.
Методика вычисления для 2002 г.
1. Составление пропорции.

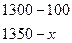

2. Вычисление показателя.
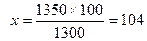
Методика вычисления для 2003 г.
1.Составление пропорции.
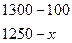
2. Вычисление показателя.
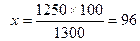 и так далее.
и так далее.
Методика вычисления для 2004 г.
1. Составление пропорции.
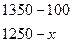
Примечание:
· относительные показатели обозначаются буквой Р;
· при учитывании градации признака обозначается показатель соответственно Р1, Р2, Р3 и т.д.;
· для большей наглядности указывается и содержание признака: Р2000 – рассчитанный по материалам 2000 г.; Р60-64 – показатель для возраста 60-64 года, Рг. – рассчитан для городского населения и т.д.
Для исключения случайных колебаний принято интенсивный показатель рассчитывать при числе явления или признака не менее 20, а при структуре явления (экстенсивный показатель) – при числе не менее 100. В иных случаях надо лучше приводить абсолютные величины или не выделять явление в отдельную группу.
· показатели наглядности обозначаются на 100;
· показатели соотношений на 10000.
Задачи
Задача 1
Первичное посещение рабочих завода в стоматологическую поликлинику по поводу санирования
| Год | Всего | Число посещений | Число санированных |
| Всего: |
Вычислить частоту и структуру обращаемости и санированных.
Задача 2
Стоматологическая помощь населению Таласской области за 2004-2007 гг.
| Годы | Обращение в стоматологическую поликлинику | |||
| Профессионального осмотр | Запломбировано зубов | Удалено зубов | Средне годовая численность населения | |
Вычислить частоту профессионального осмотра, соотношение удаленных и запломбированных зубов в стоматологической поликлинике.
Задача 3
Стоматологическая помощь населению Баткенской области за 2006-2008 гг.
| Годы | Обращение в стоматологическую поликлинику | |||
| Профессиональный осмотр | Запломбировано зубов | Удалено зубов | Средне годовая численность населения (тыс. человек) | |
| 420,7 | ||||
| 424,6 | ||||
| 428,5 |
Вычислить частоту профессионального осмотра, соотношение удаленных и запломбированных зубов в стоматологической поликлинике.
Задача 4
Стоматологическая помощь населению Иссык-Кульской области за 2006-2008 гг.
| Годы | Обращение в стоматологическую поликлинику | |||
| Профессиональный осмотр | Запломбировано зубов | Удалено зубов | Средне годовая численность населения (тыс. человек) | |
| 429,7 | ||||
| 431,7 | ||||
| 433,7 |
Вычислить частоту профессионального осмотра, соотношение удаленных и запломбированных зубов в стоматологической поликлинике.
Задача 5
Стоматологическая помощь населению Нарынской области за 2006-2008 гг.
| Годы | Обращение в стоматологическую поликлинику | |||
| Профессиональный осмотр | Запломбировано зубов | Удалено зубов | Средне годовая численность населения (тыс. человек) | |
| 267,8 | ||||
| 269,3 | ||||
| 270,6 |
Вычислить частоту профессионального осмотра, соотношение удаленных и запломбированных зубов в стоматологической поликлинике.
Задача 6
Стоматологическая помощь населению Джалал-Абадской области за 2006-2008 гг.
| Годы | Обращение в стоматологическую поликлинику | |||
| Профессиональный осмотр | Запломбировано зубов | Удалено зубов | Средне годовая численность населения (тыс. человек) | |
| 967,1 | ||||
| 977,0 | ||||
| 987,1 |
Вычислить частоту профессионального осмотра, соотношение удаленных и запломбированных зубов в стоматологической поликлинике.
Задача 7
Стоматологическая помощь населению Ошской области за 2006-2008 гг.
| Годы | Обращение в стоматологическую поликлинику | |||
| Профессиональный осмотр | Запломбировано зубов | Удалено зубов | Средне годовая численность населения (тыс. человек) | |
| 1057,0 | ||||
| 1069,3 | ||||
| 1081,3 |
Вычислить частоту профессионального осмотра, соотношение удаленных и запломбированных зубов в стоматологической поликлинике.
Задача 8
Стоматологическая помощь населению Чуйской области за 2006-2008 гг.
| Годы | Обращение в стоматологическую поликлинику | |||
| Профессиональный осмотр | Запломбировано зубов | Удалено зубов | Средне годовая численность населения (тыс. человек) | |
| 754,3 | ||||
| 758,3 | ||||
| 761,2 |
Вычислить частоту профессионального осмотра, соотношение удаленных и запломбированных зубов в стоматологической поликлинике.
Задача 9
Заболеваемость детского населения (0-14 лет) Кыргызской республики за 2007 г.
| Класс заболевания | Число заболеваний |
| Инфекционные и паразитарные | |
| Болезни уха и сосцевидного отростка | |
| Болезни крови и кроветворных органов | |
| Всего: |
Численность детей этого возраста – 1584600 человек.
Вычислить частоту и структуру заболеваний среди детей.
Задача 10
Заболеваемость населения Нарынской области КР по причинам смертности за 2007 г.
| Класс заболевания | Число заболеваний |
| Органы дыхания | |
| Органы пищеварения | |
| Органы кровообращения | |
| Болезни мочеполовой системы | |
| Всего: |
Численность населения – 269003 человек. Вычислить частоту и структуру заболеваемости.
Задача 11
Численность средних медицинских работников по регионам
Кыргызской Республики за 2006 г.
| Регион | Численность населения | Число средних медработников |
| Кыгызская республика | ||
| Чуйская область | ||
| Иссык-Кульская обл. | ||
| Нарынская обл. | ||
| Таласская обл. | ||
| Ошская обл. | ||
| Джалал-Абадская обл. | ||
| Баткенская обл. |
Вычислить показатель соотношения.
Задача 12
Численность врачей по регионам Кыргызской Республики за 2006 г.
| Регион | Численность населения | Число врачей |
| Кыгызская республика | ||
| Чуйская область | ||
| Иссык-Кульская обл. | ||
| Нарынская обл. | ||
| Таласская обл. | ||
| Ошская обл. | ||
| Джалал-Абадская обл. | ||
| Баткенская обл. |
Вычислить показатель соотношения.
Задача 13
Показатели естественного прироста в Кыргызской Республике (на 1000 чел. нас.)
| 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. |
| 12,8 | 13,2 | 13,1 | 13,8 | 14,7 |
Вычислить показатели наглядности.
Задача 14
Перинатальная смертность у детей в зависимости от возраста матери (в % к итогу)
| Возраст (лет) | Населенный пункт | |||
| А | Б | В | Г | |
| до 19 лет 20-24 25-29 30-34 35 и более | ||||
| Всего |
Вычислить и проанализировать коэффициенты правдоподобия между пунктами А и Б, В и Г, А и В, А и Г, Б и В, Б и Г.
Задача 15
Структура младенческой смертности в г. Бишкек и г.Ош за 2007 г. (в % к итогу)
| Причина | г. Бишкек | г. Ош |
| Болезни нервной системы и органов чувств | 0,6 | 2,0 |
| Инфекционные и паразитарные болезни | 2,0 | 5,0 |
| Болезни органов дыхания | 0,2 | 0,0 |
| Врожденные аномалии | 16,0 | 11,0 |
| Состояния возникающие в перинатальном периоде | 76,0 | 78,7 |
| Травмы и отравления | 0,6 | 1,7 |
Вычислить коэффициент правдоподобия.
Задача 16
Численность врачей и средних медработников в Кыргызской Республике по годам:
| Специальность | 2004 г. | 2005 г. | 2006 г. |
| Врачи | |||
| Средние медработники |
Вычислить показатель координации.
Контрольные вопросы
1. Виды относительных величин.
2. Интенсивные показатели, методика вычисления.
3. Экстенсивный показатель, методика вычисления.
4. Отличие интенсивных и экстенсивных показателей.
5. Показатели координации, методика вычисления.
6. Показатели правдоподобия, методика вычисления.
7. Показатели соотношения, методика вычисления.
8. Показатели наглядности, методика вычисления.
9. Обозначение интенсивных показателей.
10. Минимальные абсолютные числа для вычисления интенсивных и экстенсивных показателей.
Тесты
1.Относительной величиной является: а) экстенсивный показатель, б) интенсивный показатель, г) показатель соотношения, д) мода и медицина.
2.Экстенсивный показатель характеризует: а) состав явления, б) частоту явления, в) соотношение части к целому, г) структуру явления.
3. Интенсивный показатель характеризует: а) частоту явления, б) распространенность явления, в) явление в среде, г) часть явления к целому.
4. Показатель соотношения характеризует: а) отношения между разнородными величинами, б) отношения между однородными величинами, в) состав явления, г) структуру явления.
5. Показатель наглядности характеризует: а) состав явления, б) отношение явления к среде, в) отношение каждой из сравниваемых величин, г) отношение между разнородными величинами.
6. Показатели наглядности обычно рассчитываются: а) на 1000, б) на 10000, в) 100000, г) на 100.
7. Показатели соотношения рассчитываются: а) на 100, б) 1000, в) 10000, г) на 100000.
8. Показатель координации характеризует: а) соотношение частей и целого между собой, б) удельный вес, в) отношение между разнородными величинами, г) интенсивность.
9. Доля гипертонической болезни из всего числа болезней относится: а) к показателю соотношения, б) к части в целом, в) к экстенсивному показателю, г) к показателю частоты распространения явления.
10.Показатель правдоподобия это: а) числовые соотношения одноименных показателей структуры, рассчитанные на двух разных совокупностях, б) отношение между разнородными величинами, в) удельный вес явление, г) распространенность явления в среде.
11. К относительным величинам относятся: а) частота распространения, б) структура явления, в) мода, г) медиана.
12. Интенсивный показатель сравнивают: а) между собой, б) с экстенсивным показателем, в) со средними величинами, г) с частью явления.
Тема 4
СРЕДНИЕ ВЕЛИЧИНЫ
Цель изучения темы
Студент должен знать:
· вариационный ряд, его характеристику и виды;
· средние величины, их виды, применение;
· значение среднего квадратического отклонения (s) и коэффициента вариации (Сr);
Студент должен уметь:
· составлять простой и сгруппированный вариационные ряды;
· вычислять средние величины (М);
· вычислять среднее квадратическое отклонение и коэффициент вариации;
План изучения темы






