Общие решения уравнений динамики жестких систем

Задачи динамики жестких систем заключаются в том, чтобы по заданным силам или моментам определить закон движения системы (положение - x или j, скорост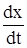и или 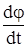и ускорения 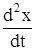или 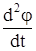в любой момент времени) или по заданному закону движения определить силы, под действием которых оно происходит.

Жесткие системы могут быть представлены в виде одной приведенной массы (момента инерции массы), движущейся под действием приведенной силы (момента).

Приведенные силы могут зависеть от координаты x, скорости 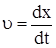и времени t. Величина приведенной массы также может быть переменной и зависеть от положения (координаты x).

Обозначим переменные приведенную силу 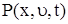и приведенную массу .

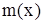При рассмотрении системы как жесткой, её элементы не деформируются при действии сил и моментов.

Пусть в момент времени отсчета t₀ скорость движения приведенной массы m равна u₀. Тогда работа внешней силы для поступательно движущейся массы равна

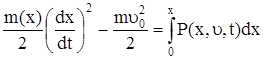, (63)

скорость движения

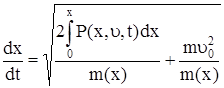, (64)

ускорение

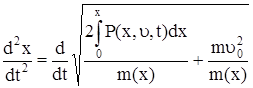, (65)

координата

. (66)

При заданных координатах из формулы (64)

, (67)

откуда

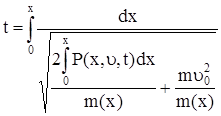. (68)

Для вращающихся масс результаты выводов аналогичны при использовании координаты j, скорости w, момента инерции массы I и момента силы в приведенных выше формулах.

Приемы интегрирования дифференциального уравнения движения жесткой системы связаны с характером функций 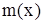, , 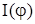, 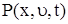. Рассмотрим некоторые конкретные примеры.

1) Масса системы ,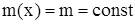

Движущая сила .

 

 

Скорость из формулы (64) будет равна

. (69)

Возведя обе части в квадрат и дифференцируя по t, найдем ускорение

, (70)

или

. (71)

Выражение (71) является вторым законом Ньютона в упрощенном виде.

Представив выражение (69) в виде

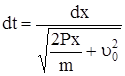, (72)

получим

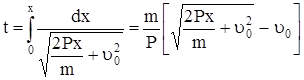, (73)

откуда

, (74)

а скорость приведенной массы

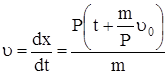. (75)

Если начальная скорость 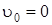, то формулы (73), (74) и (75) примут вид

, (76)

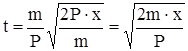, (77)

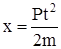. (78)

Аналогичные формулы получаются и для вращающейся массы.

2) Момент инерции массы ,

движущий момент изменяется в функции угла поворота по закону

,

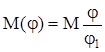где – текущая угловая координата, а

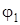– угол, соответствующий максимальному значению 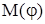, равному M, причем .

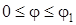Угловая скорость равна

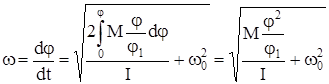, (79)

откуда

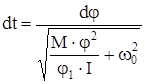, (80)

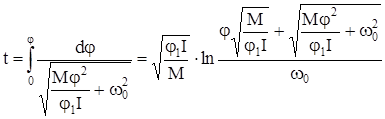. (81)

Преобразуя выражение (81), получим

, (82)

или

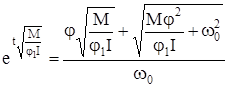, (83)

откуда

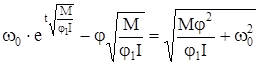. (84)

Возводя обе части равенства (84) в квадрат, решая относительно j и дифференцируя по t, получаем

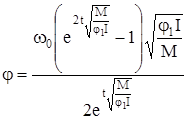, (85)

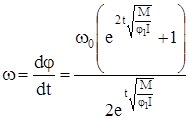, (86)

. (87)

3) Момент инерции массы , движущий момент изменяется в функции скорости .

Пусковые характеристики электродвигателей часто принимают линейными. При этом момент может быть выражен в виде

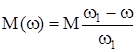, (88)

где M – наибольший приведенный пусковой момент,

– наибольшая скорость приведенной массы.

Для краткости выводов примем .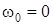

Тогда из (64)

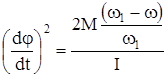, (89)

откуда

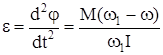, (90)

или, заменив , получим

,

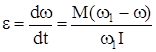откуда

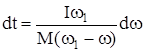(91)

и

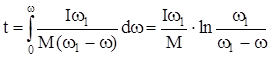. (92)

 

Решая относительно , найдем

. (93)

Дифференцируя и интегрируя, получаем

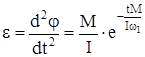, (94)

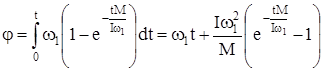. (95)

4) Момент инерции массы , движущий момент изменяется в функции времени .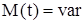

При разгоне электродвигателя с контакторным управлением

, (96)

где M – максимальный пусковой момент;

– время разгона.

Для рассматриваемого случая

, (97)

откуда аналогично предыдущим решениям получим

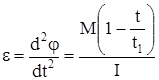, (98)

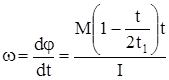, (99)

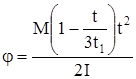. (100)