Курс лекций
Челябинск
Издательство ЮУрГУ
Содержание
Введение………………………………………………………………………………...3
1. Составление физической модели машины……………………………………..….4
2. Общие решения уравнений динамики жестких систем…………………………24
3. Общие приемы решения уравнений динамики упругих систем………………..30
4. Динамика переходных процессов ненагруженных машин……………………..32
5. Динамика переходных процессов нагруженных машин………………………..33
6. Динамика нагружения машин после разгона……………………………….……35
7. Динамические нагрузки от ударов в зазорах……………………………….……42
8. Колебания в приводных линиях…………………………………………….…….44
9. Динамика установившегося движения неравновесных систем…………….…..46
10. Колебания опорных конструкций и элементов…………………………………49
11. Определение параметров виброгасителя………………………………………..52
12. Ударное нагружение конструкций и механизмов………………………………54
13. Автоколебание систем……………………………………………………………58
14. Составление уравнений динамики систем с распределенными массами
(волновые уравнения)…………………………………………………………….59
15. Способы решения волновых уравнений…………………………………………61
16. Ударное нагружение элементов машин, представляемых в виде систем
с распределенными массами……………………………………………………..63
Введение
Металлургические машины работают в тяжелых динамических режимах. Качество этих машин в немалой степени зависит от того, насколько точно произведены расчеты их основных параметров.
Практически 90% разрушения деталей машин носят усталостный характер в результате действия динамических нагрузок. Механические колебания в машинах оказывают вредное влияние не только на прочность. Они могут в значительной степени усложнить и даже нарушить нормальный технологический процесс (например, колебание электродов дуговых электропечей, колебание валков листопрокатных станов, приводящее к ухудшению качества листов, буксование валков прокатных станов и т.д.).
Динамические расчеты машин предусматривают определение величины амплитуд и частот колебаний нагрузок в машине и на этой основе проводятся расчеты деталей на выносливость.
Большое влияние на качество машин оказывает выбор рациональных кинематических схем с возможно минимальным числом пар и звеньев без пассивных связей, обеспечивающих минимальные динамические нагрузки и большую их надежность. К основным направлениям развития современного машиностроения, обеспечивающим снижение динамической напряженности и высокое качество машин, можно отнести следующие:
– повышение мощностей, скоростей и производительности машин при одновременном улучшении их динамических характеристик и уменьшении металлоемкости;
– максимально возможное упрощение кинематических схем механизмов;
– рациональное размещение приводов отдельных механизмов в машинах с минимальной длиной приводных линий, обеспечивающее снижение динамических нагрузок и массы машин;
– упрощение конструкций механизмов путем применения индивидуальных приводов, исключая трансмиссии и муфты включения;
– использование компактных приводов типа «двигатель–редуктор», планетарных, волновых и других передач;
– применение для тяжелонагруженных машин и механизмов безредукторных приводов;
– более широкое использование гидро– и пневмоприводов, комбинированных электрогидро– и пневмогидроприводов;
– применение многодвигательных приводов.
Расчет динамических нагрузок колебательного характера в машинах включает следующие основные этапы:
1) Составление физической модели машины.
2) Определение величины и характера изменения внешних нагрузок, приложенных к системе.
3) Составление дифференциальных уравнений движения упругой системы.
4) Определение частот собственных колебаний системы.
5) Расчет упругих сил и моментов в звеньях приводов.
6) Определение действительных законов перемещения и скоростей рабочих органов машин.
СОСТАВЛЕНИЕ ФИЗИЧЕСКОЙ МОДЕЛИ МАШИНЫ
Общие положения
Всякая машина состоит из двигателя, передачи и исполнительного органа или механизма. Для определения действующих нагрузок целесообразно действительные схемы машин представлять в виде физических моделей, т.е. в приведенном виде.
В зависимости от целей исследований и конструктивных особенностей машин приведенные расчетные схемы содержат одну массу или систему сосредоточенных масс (две, три, иногда четыре), соединенных упругими звеньями, или распределенных в пределах определенных участков.
Приведенные массы могут быть по величине постоянными или переменными. Жесткость упругих звеньев и внешние силы (движущие силы и силы сопротивления) в общем случае являются переменными, зависящими от положения элементов системы и места их нагружения или скорости ведущего элемента. В некоторых случаях внешние силы выражаются в функции времени.
Точки приведения обычно выбирают в местах расположения основных масс механизма. Приведенные значения масс, находящихся по одну сторону от упругого элемента, для которого определяется расчетная нагрузка, складывают.
  |
Например, при составлении физической модели приведенной одномассовой системы для токарного станка (рис. 1), приведенный момент инерции масс к валу патрона будет состоять из приведенных значений моментов инерции масс движущихся частей электродвигателя, муфты, вращающихся элементов коробки скоростей и патрона.
Рис. 1. Одномассовая система:
M1 – момент привода; M2 – момент сопротивления;
I1 – приведенный момент инерции масс; с – приведенная жесткость элементов системы.
В качестве примера составления двухмассовой физической расчетной модели можно рассмотреть прокатный стан кварто (рис. 2).
В этом случае один из приведенных моментов инерции масс I1 будет состоять из приведенных значений моментов инерции масс якоря двигателя, муфт, вращающихся частей редуктора и шестеренной клети. Моменты инерции масс шпинделей могут быть отнесены к ведомой приведенной массе, включающей рабочие и опорные валки. В такой схеме дальнейшие расчеты позволят определить наибольшую из возможных нагрузок на шпинделях.
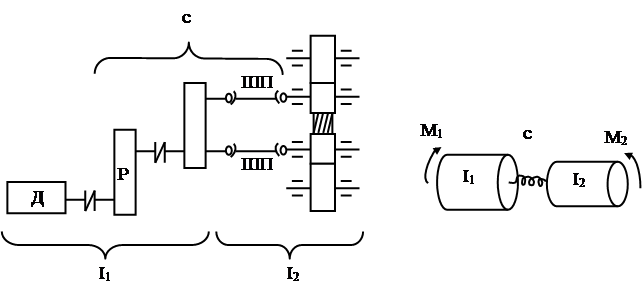
Рис. 2. Двухмассовая система
Если в состав механизма в процессе его работы входят вращающиеся и поступательно движущиеся массы, физическую модель можно представить как в виде совокупности приведенных масс, так и в виде совокупности приведенных моментов инерции масс (рис. 3).
Рис. 3. Смешанная двухмассовая модель
Переход от массы к моменту её инерции и обратно будет рассмотрен ниже.
К внешним нагрузкам машины относятся силы и моменты сил, которые оказывают сопротивление движению машины или её элементов.
Рассмотрим механизм, состоящий из двигателя и передач (рис. 4).
Требуется привести все моменты к концам вала III. Тогда приведенный момент с левой стороны вала III будет равен
,
а с правой 
.
Для вала II аналогично получим
,
.
Здесь 
, 
, 
– моменты сопротивления вращению на соответствующих валах. Если внешние нагрузки выражены в виде сил и моментов, то приведенное значение должно быть одноименным (в виде только сил или только моментов).
Силы в виде моментов или моменты в виде сил выражают через соответствующие радиусы приведения.
Например, силы сопротивления P передвижению тележки (рис. 5) необходимо привести к валу двигателя и выразить в виде момента.
 |
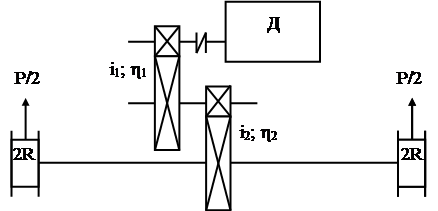Рис. 5. Схема механизма передвижения тележки
Радиус приведения в данном случае равен радиусу ходового колеса R, а приведенный момент
.
Определение моментов инерции вращающихся масс
В общем случае, для тела любой формы (рис. 6) момент инерции его массы равен
 |
.
Рис. 6. К определению момента инерции массы вращающегося тала
Для сплошного цилиндра
,
где R и D – радиус и диаметр цилиндра,
ρ – плотность материала цилиндра,
h – толщина (высота) цилиндра,
m – масса цилиндра.
Для полого цилиндра
,
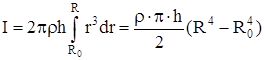где 
– диаметр отверстия (внутренний диаметр) цилиндра.
Детали типа шкив, муфта, зубчатое колесо и др. представляют собой комбинацию элементов (например, ступица, обод, зубчатый венец и т. п.). В этом случае момент инерции массы детали слагается из суммы моментов инерции масс её элементов.
В практических расчетах обычно используется формула
,
где D – наружный диаметр детали;
k – коэффициент распределения массы.
Для сплошного цилиндра k=0,125;
для полого цилиндра k=0,25;
для деталей типа шкив k=0,15.
Если известен маховой момент элемента (например, якоря двигателя), то
;
где g – ускорение свободного падения;
G – вес элемента.
