В период неустановившегося движения машины в момент упругого замыкания зазоров в линиях приводов возникают большие динамические нагрузки. Рассмотрим двухмассовую систему (рис. 21), в упругом звене которой показан суммарный приведенный зазор линии привода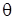 
(рад.).
Рассмотрим случай, когда якорь двигателя начал поворачиваться, а ведомая масса I2 остается еще некоторое время неподвижной, пока не выбран зазор линии 
.
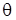Уравнение движения якоря двигателя
. (184)
При нулевых начальных условиях и постоянном пусковом моменте M1 решение имеет вид
. (185)
При равномерно ускоренном вращении якоря двигателя его скорость в конце выбора зазора равна
. (186)
После замыкания зазора система превращается в двухмассовую и дифференциальные уравнения имеют вид (133), в результате решения которых получаем
, (187)
, (188)
где
.
Начальные условия для пускового периода: 
, 
, 
.
Тогда
, 
.
Подставив значения A и B в (187) и (188), получим
, (189)
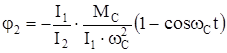. (190)
Момент в упругом звене линии привода в период соударения масс равен
. (191)
Первая составляющая в формуле (191) не зависит от зазоров в системе, поэтому рассмотрим составляющую от упругого удара в зазорах
. (192)
Подставив значение скорости якоря двигателя w3 (186) в (192), получим с учетом 
:
. (193)
Амплитуда дополнительных динамических нагрузок от упругого удара в зазорах нарастает в зависимости от величины зазора 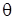по параболической кривой.
На рис. 22 показан качественный характер изменения коэффициента динамичности от величины суммарного приведенного зазора .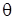
Колебания в приводных линиях
При импульсных нагрузках в линиях приводов могут возникнуть опасные колебания, которые при определенных условиях могут привести даже к разрушению механизма. Рассмотрим это явление конкретно.
Вал с одной массой
Вал, вращающийся со скоростью w, выведен из состояния равновесия возмущающей силой (импульсом силы).
При этом возникнут следующие деформации этого вала:
- 
– упругий прогиб вала;
- 
– деформация опор.
Кроме этого, следует учесть и наличие эксцентриситета вала ye. В результате центр тяжести массы m будет вращаться на расстоянии 
от первоначального (идеального) положения оси вала 0-0 (рис. 23).
Рис. 23. Вал с одной массой
На вал будут действовать две противонаправленные силы – центробежная сила и сила упругости.
Центробежная сила равна
, (194)
а сила упругости изогнутого вала
. (195)
В результате можно выделить три возможных ситуации:
– вал вернется в положение равновесия;
– критическое состояние;
– неуправляемый рост деформации вала до разрушения.
Рассмотрим ситуацию 
, которой соответствует критическая скорость вращения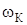 
.
В результате преобразований из равенства уравнений (194) и (195) получим
, (196)
где 
– собственная частота колебаний системы.
Если не учитывать эксцентриситет (
) и деформацию опор (
), то из (196) найдем
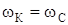. (197)
Это явление называется резонансом системы.
В свою очередь 
и 
,
где 
– возмущающая сила,
c – жесткость вала,
– жесткость опор.
Тогда
. (198)
Рассмотрим частный случай, когда не учитывается деформация опор (). Тогда из формулы (196) получим
. (199)
Характер деформации вала в зависимости от скорости его вращения показан на рис. 24. Видно, что согласно формуле (199), прогиб вала yУ по мере приближения w к wК растет и при 
становится равным 
. В закритической области 
наблюдается самоустановка вала с 
.
Для перехода через критическую область 
применяют демпфирующие устройства, позволяющие уменьшить wС за счет снижения жесткости системы c.
Вал с двумя массами
(рис. 25)
В рассматриваемом случае
. (200)
Введем обозначения:
– прогиб в сечении 1 от единичной силы в этом сечении;
(закон парности) – прогиб в сечении 1 от единичной силы в сечении 2 и то же в сечении 2 от единичной силы в сечении 1 соответственно;
– прогиб в сечении 2 от единичной силы в этом сечении.
Тогда
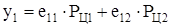, (201)
. (202)
Подставляя (201) и (202) в систему (200), получим
, (203)
. (204)
Определив отношения 
из уравнений (203) и (204) и приравняв их, запишем одно уравнение
. (205)
Решая уравнение (205), находим две критические скорости вращения вала с двумя массами
. (206)
Изложенная методика может быть использована при произвольном числе масс. Вал, несущий n масс (дисков), имеет такое же число критических скоростей вращения.
