 |
Суммарная жесткость системы складывается из приведенных жесткостей её элементов и зависит от характера их соединения (рис. 13).
Рис. 13. Схемы соединения жесткостей элементов системы:
а – параллельное; б – последовательное;
в – смешанное (параллельно-последовательное)
При параллельном соединении (рис. 13а)
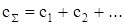(46)
При последовательном соединении (рис. 13б)
(47)
При смешанном соединении (рис. 13в)
, (48)
или
. (49)
Собственная частота колебаний системы
Простейшая динамическая система, состоящая из массы m и упругой связи c, показана на рис. 14.
Если в начальный момент времени отклонить массу на величину а и предоставить систему самой себе, то возникнут колебания, причем смещение центра тяжести массы (ЦТ) в момент времени t, будет
, (50)
где 
– круговая частота колебаний, 1/с
.
Таким образом, если в системе возбуждены колебания (импульс силы или возмущающая периодическая сила), то после снятия возмущающей силы система будет совершать свободные колебания, частота которых зависит только от параметров системы (c и m) и не зависит от величины возмущающей силы. Такие колебания называются свободными или собственными.
Если обозначить период колебаний через T, то из равенства (50) вытекает
, (51)
откуда
. (52)
Если к системе приложена внешняя периодическая сила (рис. 15)
, (53)
то возникают вынужденные колебания с частотой этой внешней силы.
Частное решение уравнения движения
, (54)
или
, (55)
где 
– сила инерции;
– сила упругости звена с,
будем искать в виде
. (56)
Подставляя зависимость (56) в равенство (55), находим
, (57)
т.е.
. (58)
После снятия возмущающей силы (
) имеем
. (59)
Для двухмассовой системы
. (60)
Для системы с вращающимися массами:
одна масса –
, (61)
две массы –
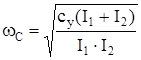. (62)
Системы делятся на высокочастотные и низкочастотные.
К высокочастотным относятся такие системы, собственные колебания которых имеют период Т в несколько раз меньший, чем время изменения внешней силы (технологическое сопротивление). К ним относится подавляющее большинство металлургических машин. Поэтому в дальнейшем будем рассматривать задачи этого класса.
Определение величины и характера изменения внешних нагрузок
Силы (моменты), действующие на машину, можно разделить на группы:
- движущие (привод);
- технологические;
- вредные сопротивления (трение и т.п.).
Движущие силы
В качестве привода может использоваться:
- гидропривод (гидроцилиндры, гидроприводы вращения);
- пневмопривод;
- электропривод (электродвигатели постоянного и переменного тока).
и другие (двигатели внутреннего сгорания, газовые и т.п.).
Многочисленные типы электродвигателей обладают различными внешними (рабочими и пусковыми) характеристиками. В зависимости от требований, предъявляемых к различным машинам, применяется тот или иной тип двигателей.
Для высокочастотных систем с некоторым приближением можно принять, что движущая сила остается постоянной.
Технологические нагрузки
Выполняемые металлургическими машинами операции весьма разнообразны (прокатка, резка металла, кантовка заготовок, подъемно-транспортные операции, кантовка сосудов с жидким металлом и т.д.). В связи с этим весьма разнообразны и характеры изменения нагрузок, а также математические зависимости их описывающие. Использование таких зависимостей при решении задач динамики систем практически невозможно из‑за их сложности, громоздкости и возникающих непреодолимых математических трудностей. В связи с этим, при решении практических задач принимаются формализованные модели характера нагружения, которые достаточно близки к реальным. Рассмотрим ряд таких моделей.
 |
1) Технологическая нагрузка прикладывается мгновенно и далее остается постоянной во времени.
Примером такого случая нагружения является подъем груза лебедкой, краном и т.п.
 |
2) Технологическая нагрузка изменяется в функции времени
При линейной зависимости момента от времени, его текущее значение равно
,
а при использовании экспоненциального закона (б)
,
где e – основание натурального логарифма;
A – показатель экспоненты, определяющий интенсивность нарастания технологической нагрузки.
 |
3) Технологическая нагрузка изменяется в функции угла поворота
Законы изменения M аналогичны варианту 2).
4) Технологическая нагрузка изменяется периодически по гармоническому закону, например,
.
5) Импульсное (ударное) приложение технологической нагрузки.
