Реальное пространство, которое мы будем изучать, называется трехмерным R3. Каждая точка в нем определяется тройкой действительных чисел. Плоскость – R2.
Декартова прямоугольная система координат представляет собой три взаимно перпендикулярные оси в пространстве с общим началом О и одинаковой масштабной единицей:
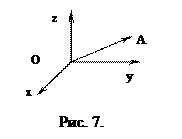
ось Оx – ось абсцисс;
ось Оy – ось ординат;
ось Оz – ось аппликат.
Направление осей координат можно задать единичными векторами (ортами) 
, 
, 
.
Возьмем произвольную точку М. Вектор 
называется радиус-вектором точки М: 
. Радиус-вектор, в свою очередь, определяет некоторый вектор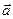 
, который можно переносить в пространстве параллельно самому себе. Найдем проекции вектора на оси координат: очевидно, что
Такая картинка называется разложением вектора по трем координатным осям. Проекции радиус вектора на координатные оси обозначим через x, y, z.
Координатами точки М в пространстве называются проекции вектора на соответствующие координатные оси: M (x, y, z).
Пользуясь свойствами проекций, с помощью единичных векторов , , можно записать: 
; 
; 
. Тогда
или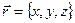 
. (6.1)
Проекции вектора на координатные оси называются координатами вектора.
Таким образом, три числа x, y, z, с одной стороны, являются координатами точки М, с другой – координатами радиус-вектора этой точки. Равенство (6.1) – основное равенство векторной алгебры. Его называют разложением вектора 
по координатным осям (по базису , , ).
Система координат в пространстве устанавливает взаимно однозначное соответствие между точками пространства и тройками упорядоченных чисел (или радиус-векторами).
Обозначим 
, 
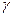- углы наклона вектора 
к осям Ox, Oy, Oz. Числа 
, 
, 
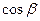принято называть направляющими косинусами вектора .
Из определения проекций пол4учим
; 
; 
(6.2
Учитывая, что - диагональ прямоугольного параллелепипеда, имеем определение длины вектора через его координаты
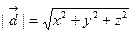(6.3)
(6.4)
Из системы (7.4) следует, что сумма квадратов направляющих косинусов любоговектора равна 1
Вектор однозначно определяется заданием его длины и
трех направляющих косинусов.
Действия над векторами в координатах.
Пусть даны координаты двух радиусов-векторов 
и 
или 
и 
1. два радиус-вектора равны 
тогда и только тогда, когда равны их координаты
2. Чтобы умножить радиус-вектор на число, надо каждую из его координату умножить на это число:
или 
, т.к.
и т.д. – по первому свойству проекций.
3. Чтобы сложить (вычесть) два радиус-вектора, надо сложить (вычесть) их одноименные координаты.
или 
;
т.к. 
и т.д. – по второму свойству проекций.
Координаты вектора
Пусть даны координаты точек 
и 
.
Найдем координаты вектора 
. Рассмотрим радиус-векторы: 
и 
.
Очевидно, что
. В координатной форме:
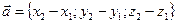. (6.5)
Следовательно, чтобы найти координаты вектора 
, нужно из координат его конца вычесть координаты начала.
