Определение угла между прямыми сводится к определению угла между их направляющими векторами 
; 
.
Из определения скалярного произведения имеем:
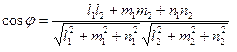(12.5)
Условие параллельности прямых эквивалентно условию коллинеарности их направляющих векторов 
и 
:
(12.6)
Условие перпендикулярности: (, ) = 0:
l1l2 + m1m2 +n1n2 = 0 (12.7)
Пример 12.4. Найти угол между прямой, проходящей через две точки 
и прямой
.
Решение. Координаты направляющего вектора первой прямой 
. Для второй прямой направляющим является вектор 
. Угол между направляющими векторами вычислим, используя формулу (12.5),
.
Вопросы для самопроверки
1. Как записывается общее уравнение прямой в пространстве?
2. Как записываются параметрические уравнения прямой в пространстве?
3. Как записываются уравнения прямой, проходящей через две точки в пространстве?
4. Как вычисляются углы между двумя прямыми в пространстве?
5. Каковы условия параллельности и перпендикулярности двух прямых в пространстве?
Задачи для самостоятельного решения
1.Исследовать взаимное расположение следующих пар прямых в пространстве
1) 
и 
2) 
и 
3) 
и 
4) 
и 
Ответ. 1) совпадают; 2) параллельны; 3) скрещиваются; 4) пересекаются.
2. Составить параметрические уравнения прямой: 
Ответ. 
3. Написать параметрические уравнения прямой, проведенной через начало координат перпендикулярно плоскости 
Ответ. 
4. Составить канонические уравнения прямой, проходящей через точку М 1(2; 0 -3) параллельно: 1) вектору 
2) прямой 
3) оси Ох; 4) оси Оу; 5) оси Оz.
Ответ. 1) 
2) 
3) 
4) 
5) 
5. Через точки 
и 
проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.
Ответ. 
, 
, 
.
6. Даны вершины треугольника А (3; 6; -7), В (-5; 2; 3)и С (4; -7; -2). Составить параметрические уравнения его медианы, проведенной из вершины С.
Ответ. 
7. Даны вершины треугольника А (2; -1; -3), В (5; 2; -7)и С (-7; 11; 6). Составить канонические уравнения биссектрисы его внешнего угла при вершине А.
Ответ. 
8. Даны вершины треугольника А (1; -2; -4), В (3; 1; -3)и С (5; 1; -7). Составить параметрические уравнения его высоты, опущенной из вершины В на противоположную сторону.
Ответ. 
9. Составить канонические уравнения следующих прямых:
1) 
2) 
Ответ. 1) 
2) 
10. Доказать параллельность прямых:
1) 
и 
2) 
и
11. Доказать перпендикулярность прямых:
1) 
и 
2) 
и
12. Найти тупой угол между прямыми
и 
.
Ответ. 135°
13. Даны прямые
и 
;
при каком значении m они пересекаются?
Ответ. m = 3.
14. Составить уравнение прямой, которая проходит через точку М (-4; -5; 3) и пересекает две прямые
, 
.
Ответ. 
Занятие 13.Смешанные задачи, относящиеся к уравнению плоскости и уравнениям прямой
