Формулы Крамера просты по своей записи, но при больших n они приводят к громоздким вычислениям. Кроме того, они, в основном, используются, когда число уравнений равно числу неизвестных и 
.
При решении систем, содержащих более трех уравнений, гораздо удобнее использовать метод последовательного исключения переменных (метод Гаусса). Пусть дана система:
(4.1)
Элементарными преобразованиями системы называются следующие операции:
1. умножение обеих частей одного из уравнений системы на произвольное число 
.
2. прибавление к обеим частям одного из уравнений соответствующих частей другого уравнения, умноженного на число 
.
3. перестановки уравнений в системе.
Очевидно, что в результате каждой из этих операций система (4.10) перейдет в систему, эквивалентную исходной.
Выпишем матрицу системы (4.1):
Если в системе (4.1) выполнено преобразование (2), то получим новую систему с матрицей В|, причем В| получается из В следующим образом: к некоторой строке матрицы В прибавляется другая строка, умноженная на λ; и т.д..
Поэтому вместо того, чтобы писать новую систему уравнений, пишут соответствующую ей матрицу В. При этом возможны следующие случаи:
1. Система преобразуется к «треугольному виду», тогда она имеет единственное решение.
2. В преобразованной системе число уравнений может оказаться меньше числа переменных. Такая система преобразуется к «трапецевидной» форме. Система (4.1) имеет бесчисленное множество решений.
3. В ходе исключения получается противоречивое уравнение. Тогда система (4.1) несовместна.
Пример 4.1. Решить систему уравнений:
Решение. Расширенная матрица системы
~
Умножаем каждый элемент 1-й строки на(-3) и складываем со 2-й строкой. Умножаем каждый элемент 1-й строки на(-2) и складываем с 3-й строкой. Получаем:
~ Умножаем каждый элемент 2-й строки на (
) и складываем с 3-й строкой. Получаем:
~ 
.
Матрица привелась к «треугольному» виду. Система имеет единственное решение. Вернемся к системе уравнений.
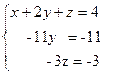
Из последнего уравнения получим z = 1. Подставим найденное значение во второе уравнение, найдем y =1, а затем в первое. Таким образом, поднимаясь по системе от последнего уравнения к первому, найдем ее решение.
Решение системы: z = 1; y =1; x =1.
Пример 4.2. Решить систему уравнений:
Решение. Расширенная матрица системы
~ Умножаем каждый элемент 1-й
строки на(-3) и на (-4) и сложим со второй и третьей строкой соответственно. Получим:
~ 
~ Умножаем каждый элемент 2-й
строки на(-1) и сложим с 3-й. Получим:
~ 
.
Третье уравнение системы противоречиво. С другой стороны,
ранг матрицы системы r(A)=2, ранг расширенной матрицы r(A/B)=3, r(A)≠r(A/B), следовательно, система несовместна.
Пример 4.3. Решить систему уравнений:
Решение. Расширенная матрица системы
~ 
~ 
~ 
,
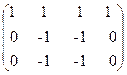Матрица привелась к «трапецевидной» форме
r(A)=2; r(A/B)= 2 => система совместна и имеет бесчисленное множество решений. Тогда
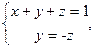
Пусть z = t, t - любое число, тогда x = 1, y = -t, z = t, t – любое число.
Однородная система имеет либо единственное тривиальное решение, т.е. x = y = z = 0, если 
≠0 и ранг матрицы равен числу неизвестных, причем число неизвестных равно числу уравнений, либо имеет бесчисленное множество решений в противном случае.
Вопросы для самопроверки
1. Опишите метод Гаусса решения систем линейных уравнений.
