Условие принадлежности прямой к плоскости. Пересечение прямой и плоскости

Условие принадлежности прямой кплоскости выражается двумя равенствами

, (13.5)

первое из которых означает, что точка (x ₁ ,y ₁ ,z ₁ ), через которую проходит прямая, принадлежит плоскости, а второе- это условие параллельности прямой и плоскости.

Координаты точки пересечения прямой и плоскости Ax+By+Cz+D=0 определяются из системы уравнений

(13.6)

Пример 13.4. Доказать, что прямая

лежит в плоскости

3 x +2 y -4 z -23=0.

Решение. Воспользуемся формулой (4.5)

.

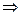
Следовательно, прямая лежит в данной плоскости.

Пример 13.5. Найти точку пересечения плоскости и прямой

Решение. Решим совместно систему уравнений прямой и плоскости. Подставим выражение для в уравнение плоскости

После упрощения получим откуда Из уравнения прямой при находим координаты точки пересечения Таким образом, искомой точкой пересечения является точка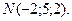

Пример 13.6. Дана прямая и вне ее точка М (1; 1; 1). Найти точку N, симметричную точке М относительно данной прямой.

Решение. Составим уравнение плоскости, проектирующей точку М на данную прямую, в виде

Используя условие перпендикулярности заданной прямой и проектирующей плоскости , находим уравнение плоскости

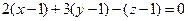
или

.

Найдем проекцию точки М на прямую, для чего совместно решим систему уравнений

Запишем уравнения прямой в параметрическом виде

Подставляя x, y, z в уравнение плоскости, найдем t =1/14. Отсюда x = 8 / 7, y =3/ 14, z = - 15/14.

Тогда координаты симметричной точки можно найти из формул середины отрезка, т.е.

,

или

,

откуда , , . Следовательно,

N (9/7; - 4/7; - 22/7).

Пример 13.7. Вычислит расстояние d точки Р (1 -1;-2) от прямой

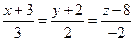
Решение 1. Выберем на прямой какую-нибудь точку, например М ₁(-3; -2; 8). Будем считать, что направляющий вектор прямой приложен в точке М ₁. Модуль векторного произведения векторов и определит площадь параллелограмма, построенного на этих векторах; высота этого параллелограмма, проведенная из вершины Р, будет являться искомым расстоянием d. Следовательно, для вычисления расстояния d имеем формулу . Теперь вычислим координаты вектора , зная координаты его конца и начала: = . Найдем векторное произведение векторов и : . Определим его модуль . Вычислим модуль вектора : 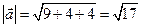. Найдем искомое расстояние .

Решение 2. Составим уравнение плоскости, проектирующей точку Р на данную прямую, в виде

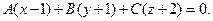
Используя условие перпендикулярности заданной прямой и проектирующей плоскости , находим уравнение плоскости .

Найдем точку М пересечения прямой с построенной плоскостью. Для этого запишем уравнения прямой в параметрическом виде

Подставляя x, y, z в уравнение плоскости, найдем t = 2. Отсюда x = 3, y =2, z = - 4. Расстояние между точками Р и М будет являться искомым расстоянием d. Следовательно

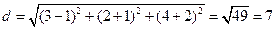
Пример 13.8. Вычислить кратчайшее расстояние между двумя прямыми

;. .

Решение. Данные прямые являются скрещивающимися и лежат в параллельных плоскостях. Через прямую l ₂проведем плоскость параллельную прямой l ₁. В качестве нормального вектора возьмем , где и - направляющие векторы прямых.

=

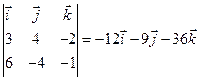
Зная точку на прямой l ₂ - М ₂(21;-5; 2), запишем уравнение плоскости в виде

или

.

Расстояние от точки М ₁(-7; -4; -3) на прямой l ₁ и будет искомым расстоянием:

.

Вопросы для самопроверки

1. Как вычисляются углы между плоскостью и прямой?

2. Каковы условия параллельности и перпендикулярности прямой и плоскости?

3. Как проверить, что прямая принадлежит плоскости?

4. Как найти точку пересечения прямой с плоскостью?

5. Как найти расстояние между параллельными прямыми, между скрещивающимися прямыми?