Основные свойства определителей
Понятие определителя
Любой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем или детерминантом n -го порядка этой матрицы. Начнем с определителей второго и третьего порядков.
Пусть дана матрица
А= 
,
Тогда ее определитель второго порядка вводится по формуле
det A = 
= 
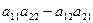(1.1)
Правило вычисления определителя второго порядка очевидно: из произведения элементов стоящих на главной диагонали вычитается произведение элементов стоящих на второй диагонали матрицы А.
В дальнейшем мы не будем приводить матрицу, для которой вычисляется определитель, так как в записи определителя содержится все элементы соответствующей матрицы.
Определитель третьего порядка вычисляется по формуле
(1.2) Правило вычисления определителя третьего порядка таково. Это алгебраическая сумма шести тройных произведений элементов, стоящих в разных строках и разных столбцах; со знаком “плюс” берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали; со знаком “минус” – произведения, сомножители которых стоят не на главной диагонали и в вершинах треугольников с основаниями, параллельными этой диагонали (рис. 1).
 |
Порядок определителя равен порядку соответствующей матрицы.
Основные свойства определителя
1. Величина определителя не изменяется, если строки и столбцы этого определителя поменять ролями, т. е.
= 
.
2. Перестановка двух строк (или двух столбцов) определителя равносильно уменьшению его на число (-1).
3. Если определитель имеет две одинаковые строки (или столбца), то он равен нулю.
4. Умножение всех элементов некоторой строки (столбца) определителя на число 
равносильно умножению определителя на это число , т. е. общий множитель всех элементов некоторой строки (столбца) определителя можно выносить за знак определителя:
= 
.
5. Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю.
6. Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.
7. Если каждый элемент n -ой строки (столбца) представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы определителей. Первый из которых имеет в n -ой строке (столбце) первые из упомянутых слагаемых и те же элементы, что и исходный определитель в остальных строках (столбцах), а второй определитель имеет в n -ой строке (столбце) вторые из упомянутых слагаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах):
= 
+ 
.
8. Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель, то величина определителя не изменится.
= 
+ 
, 
=0.
Минором элемента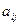 
определителя n -го порядка называется определитель (n -1)-го порядка, получаемый из данного определителя путем вычеркивания той строки и столбца, на пересечении которых стоит данный элемент. Это число 
.
Алгебраическим дополнением любого элемента определителя называется число, равное минору этого элемента, взятому со знаком (+), если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, есть число четное и со знаком (-) – в противном случае
(2.3)
; 
; 
.
9. Разложение определителя по строке (столбцу ) (Один из способов вычисления определителя) Сумма произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения элементов этой строки (столбца) равна величине этого определителя.
Определитель 3-го порядка разложим по первой строке
= 
- 
+ 
;
Пример 1.1. Вычислить определитель четвертого порядка
.
Разложить определитель можно по любой строке (столбцу). Однако объем вычислений можно существенно уменьшить, если выбрать такую строку (столбец), в которой больше элементов, равных нулю. Наиболее подходящей в нашем случае является вторая строка. Разложение по ней определителя имеет вид
=
=3(3 +14 + 48 – 126 – 2 - 8) + 2(4 + 24 + 36 - 48 - 9 - 4)= -207.
10. Сумма произведений элементов 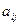некоторой строки (столбца) определителя на соответствующее алгебраическое дополнение другой строки (столбца) равна нулю.
11. Произведение двух определителей n -го порядка с элементами 
есть в свою очередь определитель
n -го порядка с элементами 
:
.
12. При транспонировании матрицы определитель не меняется.
Вопросы для самопроверки
1. Что называется определителем? Каковы основные свойства определителя?
2.. Что называется минором и алгебраическим дополнением? Приведите примеры.
3. Каковы способы вычисления определителей? Приведите примеры.
