1.
| 2.
|
3 
| 4. 
|
5.
| 6.
|
7.
| 8.
|
9.
| 10.
|
11.
| 12.
|
13.
| 14.
|
15.
| 16.
|
17.
| 18.
|
19.
| 20.
|
21.
| 22.
|
23.
| 24.
|
25.
| 26.
|
27.
| 28.
|
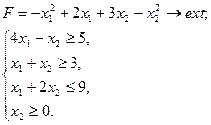
29.
| 30.
|
Задача 6. Розв’язати задачу нелінійного програмування методом множників Лагранжа
1.
| 2.
|
3.
| 4.
|
5.
| 6.
|
7.
| 8.
|
9.
| 10.
|
11.
| 12.
|
13.
| 14.
|
15.
| 16.
|
17.
|
 .
|
19.
| 20.
|
21.
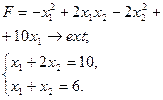
| 22.
|
23.
| 24.
|
25.
| 26.
|
27.
| 28.
|
29.
| 30.
|
Задача 7. В таблиці наведено відомості про використання балансу за звітний період, тис. грн. (V – номер варіанту)
| Галузь | Споживання | Кінцевий продукт | Валовий випуск | ||
| Виробництво | 160+V | 500+V | |||
| 275+V | 400+V |
Обчислити необхідний валовий дохід випуску кожної галузі, якщо кінцевий продукт першої галузі повинен збільшитися у 
раз, а другої галузі – на 
%.
| ||||||||||
|
| 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | 2,1 |
|
| ||||||||||
|
| ||||||||||
|
| 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 | 3,1 |
|
| ||||||||||
|
| ||||||||||
|
| 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 | 4,1 |
|
|
Задача 8. Розв’язати задачу дробово-лінійного програмування
1. 
| 2. 
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9.
| 10.
|
11.
| 12.
|
13.
| 14.
|
15.
| 16.
|
17.
| 18.
|
19.
| 20.
|
21.
| 22.
|
23.
| 24.
|
25.
| 26.
|
| 27.
| 28.
|
29.
| 30.
|
Задача 9. Нехай керівництво підприємства розглядає пропозицію про вкладання коштів у 4 структурних підрозділи. Запропоновано вкласти 100 тис. грн. у ці напрямки так, щоб одержати максимальний сумарний приріст випуску продукції.
Значення 
приросту випуску продукції у пі підрозділи в залежності від виділеної суми 
наведено у таблиці
| Кошти, тис. грн. | Приріст випуску продукції, тис. грн. | |||
1+ 
| 1+ 
| |||
| +32
| ||||
| +46
|
ЗРАЗКИ РОЗВ’ЯЗАННЯ ЗАДАЧ
Задача 1.
Підприємство виробляє два види продукції. Для виготовлення першого виду продукції використовують два види ресурсів: сировина і електроенергія, витрати яких на одиницю продукції і місячні запаси наведено у таблиці.
| Вихідний ресурс | Витрати вихідного ресурсу на одиницю продукції, грн. | Запаси, грн. | |
| І вид | ІІ вид | ||
| Сировина | 0,8 | 0,5 | |
| Електроенергія | 0,4 | 0,8 |
Вивчення ринку збуту показало, що місячний попит на І вид продукції перевищує попит на ІІ вид не більше ніж на 100 кг. Окрім того, встановлено, що попит на І вид продукції не перевищує 350 кг за місяць. Роздрібна ціна одиниці продукції І виду - 16 грн., а ІІ – 14 грн.
Яку кількість кожного виду продукції 
повинно щомісяця виробляти підприємство, щоб виручка 
від реалізації продукції була максимальною?
Розв’яжемо задачу за допомогою графічного методу
Позначимо: через 
- місячний обсяг випуску продукції І виду, кг; через 
- місячний обсяг випуску продукції ІІ виду, кг.
Складемо економіко-математичну модель задачі.
За критерій оцінки приймемо виручку від реалізації продукції (В), яка визначається за формулою
,
де 
- ціна одиниці і -го виду продукції, грн.; 
- обсяги виробленої продукції, кг.
Цільова функція буде мати вигляд
при обмеженнях
Знайдемо область припустимих розв’язків.
1. 
, 
2. 
, 
3. 
, 
4. 
5. 
- І чверть.
Областю припустимих розв’язків є п’ятикутник 
.
Для знаходження екстремальних значень цільової функції при графічному розв’язку знайдемо вектор 
, який є градієнтом функції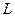 
.
Проводимо лінію рівня 
, яка є перпендикулярною до вектора . Оскільки цільова функція досліджується на максимум, то переміщується лінія рівня за напрямком вектора . Точкою виходу з області припустимих значень є точка 
, координати якої визначаються як перетин прямих та . Розв’язком системи є значення 
кг і 
кг.
Таким чином, найбільше значення функції або максимальна виручка від реалізації продукції складе
Задача №2
Підприємство виробляє три види продукції. Для виготовлення кожного виду продукції використовують два види ресурсів: сировина і електроенергія, витрати яких на одиницю продукції і місячні запаси наведено у таблиці.
| Вихідний ресурс | Витрати вихідного ресурсу на одиницю продукції, тис. грн. | Запаси, тис. грн. | ||
| І вид | ІІ вид | ІІІ вид | ||
| Сировина | ||||
| Електроенергія |
Роздрібна ціна одиниці продукції І виду - 3 тис. грн., ІІ виду – 4 тис. грн., ІІІ виду – 2 тис. грн.
Яку кількість кожного виду продукції повинно щомісяця виробляти підприємство, щоб виручка 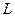від реалізації продукції був максимальним?
Розв’яжемо задачу за допомогою симплексного методу
при обмеженнях
Переведемо економіко-математичну модель до канонічного вигляду
Складемо симплексну таблицю першого кроку
| БЗ | 
| |||||
|
|
| 
| 
| 
| |||
|
| |||||||
|
| 2 | ||||||
| -3 | -4 | -2 |
Заповнимо індексний рядок для змінних за формулами
і для вільного члена
.
Оскільки, маємо від’ємні оцінки 
при умові, що цільова функція 
, то знайдений розв’язок не є оптимальним. Складемо симплексну таблицю другого кроку.
За ключовий стовпець обираємо четвертий стовпець, який відповідає найменшому значенню індексної оцінки -4, а за індексний елемент 2, тому що найменше значення відношення вільного члена до відповідного елемента ключового стовпця 
.
|
| БЗ |
| |||||
|
|
|
|
|
| |||
|
| 
| 
| 
| ||||
|
| 
|
|
| ||||
|
| -1 |
Оскільки, маємо від’ємну оцінку при умові, що цільова функція , то знайдений розв’язок не є оптимальним. Складемо симплексну таблицю третього кроку.
За ключовий стовпець обираємо третій стовпець, який відповідає від’ємному значенню індексної оцінки -1, а за індексний елемент , тому що найменше значення відношення вільного члена до відповідного елемента ключового стовпця 
.
|
| БЗ |
| |||||
|
|
|
|
|
| |||
|
| 
| 
| 
| 
| |||
|
|
|
| 
| 
| |||
|
|
|
| 
| 
|
