Деякі задачі лінійного програмування вимагають цілочислового розв’язку. До них відносяться задачі з виробництва і розподілу не діленої продукції (випуск верстатів, телевізорів, автомобілів тощо). У загальному вигляді математична модель задачі цілочислового програмування має вигляд 
з обмеженнями
Оптимальний розв’язок задачі, яку знайдено симплексним методом, часто не є цілочисловим. Його можна округлити до найближчого цілого числа. Але таке округлення може дати розв’язок, який не є найкращим серед цілочислових розв’язків або привести до розв’язку, що не задовольняє системі обмежень. Тому для знаходження цілочислових розв’язків необхідний особливий алгоритм. Такий алгоритм запропонував Гоморі.
Метод Гоморі
Метод Гоморі полягає у наступному. Симплексним методом знаходять оптимальний розв’язок задачі. Якщо розв’язок цілочисловий, тоді задача розв’язана. Якщо ж він вміщує хоча б одну дробову координату, тоді закладають додаткове обмеження за цілочисельністю і обчислення продовжують до одержання нового рішення. Якщо ж і воно є не цілочисловим, тоді знову накладають нове обмеження за цілочисельністю. Обчислення продовжують до тих пір, доки не буде одержаний цілочисловий розв’язок або показано, що задача не має цілочислового розв’язку.
Нехай одержано оптимальний розв’язок 
, який не э цілочисловим, тоді останній крок можна представити у вигляді симплексної таблиці, де 
- ранг системи обмежень; 
- коефіцієнт симплексної таблиці 
-го рядка 
-го стовпця; 
- вільний член -го рядка.
| ... | ... | 
| ... | 
| 
| ||||
| ... | ... | 
| ... | 
| 
| ||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| ... | ... | 
| ... | 
|
| ||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| ... | ... | 
| ... | 
| 
|
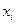
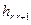
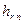
Нехай і хоча б одне з 
(
) – дробові числа.
Позначимо через 
і 
цілі частини чисел і .
Цілою частиною числа називається найбільше ціле число, яке не перевищує .
Позначимо через 
і 
цілі частини чисел і .
Дробовою частиною чисел і називається різниця 
та 
.
П риклад:
Якщо всі і хоча б одне значення дробові, то з урахуванням введених позначень цілих і дробових чисел, додаткове обмеження за цілочисельністю прийме вигляд
Зауваження:
1. Якщо (вільний член) – дробове число, а всі коефіцієнти - цілі числа, тоді задача лінійного програмування не має цілочислового розв’язку.
2. Обмеження цілочисельності може бути накладене не на всі змінні, а лише на їх частину. У цьому випадку задача є частково цілочисловою.
Графічний метод
При наявності у задачі лінійного програмування двох змінних, а в системі обмежень – нерівностей, вона може бути розв’язана графічним методом.
У системі координат знаходять область припустимих розв’язків (ОПР), будують вектор 
і лінію рівня, яка є перпендикулярною до вектора . Переміщуючи лінію рівня за напрямком вектора для задач на максимум, знаходять найбільш віддалену від початку координат точку і її координати.
У випадку, коли координати цієї точки не є цілочисловими, у ОПР будують цілочислову сітку і знаходять в ній такі цілі числа, які задовольняють системі обмежень і при яких значення цільової функції є найбільш близьким до екстремального не цілочислового розв’язку. Координати такої вершини і є цілочисловим розв’язком.
НЕЛІНІЙНЕ ПРОГРАМУВАННЯ
