Розв’язком задачі Коші для диференціального рівняння 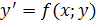
є функція, що задовольняє рівняння та початкову умову y(x0)=y0. Наближення згідно означення похідної у рівнянні виразом y ’≈(уi+1-yi)/h, де
h= x n+1 - x n, дозволяє одержати формулу Ейлера послідовного обчислення значень функції для розв’язку задачі Коші:
 .
.
Покажемо на прикладі як використовуючи метод Ейлера, виконати перші п’ять кроків наближення значення розв’язку задачі Коші для диференціального рівняння першого порядку:
 при h= x n+1 - x n = 0,2 з початковою умовою x0= 0; y0= 1.
при h= x n+1 - x n = 0,2 з початковою умовою x0= 0; y0= 1.
З початкової умови маємо значення x0= 0; y0= 1. Тоді


Продовжуючи одержуємо значення розв’язку:
| i | x | y |
| 0,2 | 1,40 | |
| 0,4 | 1,98 | |
| 0,6 | 2,83 | |
| 0,8 | 4,11 | |
| 6,01 |
Проте метод Ейлера має похибку порядку h, а отже на практиці використовують модифікації цього методу, що одержали назву методів Рунге-Кута:
 ;
;
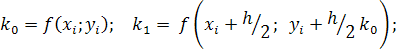

Використовуючи метод Рунге-Кута, виконати перші кроки обчислення значень розв’язку задачі Коші для диференціального рівняння першого порядку:
 при h= x n+1 - x n = 0,5. Початкова умова x0= 0; y0= 1.
при h= x n+1 - x n = 0,5. Початкова умова x0= 0; y0= 1.
З початкової умови x0= 0; y0= 1. Тоді 

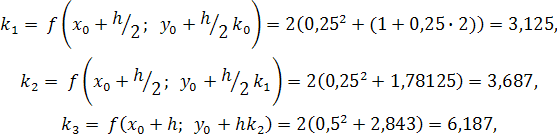

Продовжуючи одержуємо значення розв’язку:
| i | x | y |
| 0,5 | 2,818 | |
| 8,522 | ||
| 1,5 | 25,606 | |
| 61,104 |
Пакет Maple дозволяє будувати як загальний розв’язок диференціальних рівнянь так і розв’язок задачі Коші оператором
dsolve ();
Зокрема, для побудови загального розв’язку диференціального рівняння  оператор
оператор

дозволяє одержати розв’язок
 .
.
У випадку задачі Коші записуємо

одержуючи розв’язок
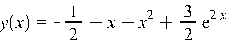 .
.
Графіки розв’язків задачі Коші при різних початкових умовах (інтегральні криві диференціального рівняння) будуємо оператором

На графіку бачимо три інтегральні криві, що є розв’язками диференціаль-ного рівняння  при початкових значеннях -2;1;3.
при початкових значеннях -2;1;3.

Рис. 4.
Проте в багатьох випадках функція, що є розв’язком задачі Коші не записується у явній формі і може визначатись лише числовими методами.
Такий розв’язок будується у формі відповідної процедури.

Після вводу одержуємо

Сформовану процедуру можна використовувати для обчислення значень. Зокрема рядок

дає значення


 .
.
За потреби значення числового розв’язку можна вивести масивом

Одержуючи таблицю значень розв’язку задачі Коші:

Завдання 6
Використовуючи метод поділу навпіл, обчислити перші три кроки наближення кореня рівняння  на проміжку
на проміжку  . Обчислення проводити з точністю 0,01. Результат записати визначивши середню точку тричі звуженого інтервалу.
. Обчислення проводити з точністю 0,01. Результат записати визначивши середню точку тричі звуженого інтервалу.
Спочатку необхідно пересвідчитись,що проміжок  містить лише один корінь рівняння:
містить лише один корінь рівняння:  . Це можна виконати шляхом табулювання значень функції чи графічно. Функція
. Це можна виконати шляхом табулювання значень функції чи графічно. Функція  один раз міняє знак на проміжку
один раз міняє знак на проміжку  .
.
Для заданої функції  проміжку
проміжку  умова виконується.
умова виконується.
| x | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 | |
| y | -1 | -1,27 | -0,86 | 0,296 | 2,232 | 5 | |
| |||||||
Рис. 5
Згідно методу поділу навпіл (діхотомії) на кожному кроці наближення визначається середня точка  інтервалу
інтервалу  . З одержаних таким поділом частин залишаємо відрізок на кінцях якого функція міняє знак. Якщо виконується умова
. З одержаних таким поділом частин залишаємо відрізок на кінцях якого функція міняє знак. Якщо виконується умова

то обираємо  .
.
В протилежному випадку  .
.
Використаємо запропоновану ітераційну схему.


Умова  не виконується отже
не виконується отже 
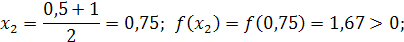
 .
.
Умова  виконується отже
виконується отже 

 .
.
Умова  виконується отже
виконується отже 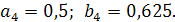
Четверте наближення кореня рівняння 
вважаємо достатнім при запропонованій точності
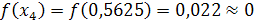 .
.
Приймаємо корінь рівняння: 
Завдання 7
Визначити точку мінімуму функції двох змінних
 .
.
За допомогою градієнтного методу найшвидшого спуску, виконати два кроки наближення.
Знайдемо вектор градієнта, що визначає напрям найшвидшої зміни функції:
 .
.
Оскільки відомо, що задана функція може мати лише одну екстремальну точку початкове наближення вибираємо довільно

Методом найшвидшого спуску наступне наближення обчислюємо за формулою 
Виконаємо перший крок наближення:
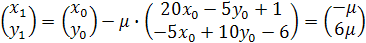 ,
,

Визначаючи значення параметра  мінімізуємо одержану функцію однієї змінної. Очевидно
мінімізуємо одержану функцію однієї змінної. Очевидно

Перше наближення:  і
і 
Виконаємо другий крок.
 ,
,

Значення параметра  визначаємо з умови мініму одержаної функції.
визначаємо з умови мініму одержаної функції.

Друге наближення:  і
і  .
.
Зауважимо, що довжина вектора градієнту на кожному кроці зменшується, що є ознакою наближення до точки екстремуму.Необхідна умова екстремуму  .
.
Для заданої в умові функції з необхідної умови екстремуму, що складає систему двох лінійних ріинянь, легко визначити координати точки екстремуму:  і оцінити ефективність обчислених наближень:
і оцінити ефективність обчислених наближень: 
 .
.







