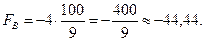Оскільки, всі оцінки  при умові, що цільова функція
при умові, що цільова функція  , то знайдений розв’язок є оптимальним.
, то знайдений розв’язок є оптимальним.

Таким чином, підприємству необхідно виробляти продукцію І і ІІ виду, а випуск продукції ІІІ виду припинити.
Задача №3
На складах  зосереджені запаси продукції у кількості 90, 400, 110 тон відповідно. Споживачі
зосереджені запаси продукції у кількості 90, 400, 110 тон відповідно. Споживачі  повинні одержати цю продукцію у кількості 140, 300, 160 тон відповідно. Знайти такий варіант закріплення постачальників до споживачів, при якому сума витрат на перевезення була б мінімальною.
повинні одержати цю продукцію у кількості 140, 300, 160 тон відповідно. Знайти такий варіант закріплення постачальників до споживачів, при якому сума витрат на перевезення була б мінімальною.
Витрати на перевезення однієї тони продукції задано матрицею  .
.
Перевіримо, чи є дана задача закритою.
 тон;
тон;
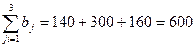 тон.
тон.
 .
.
Отже, дана транспортна задача є закритою.
Знайдемо вихідний опорний розв’язок методом мінімального тарифу.
Кількість зайнятих клітин дорівнює 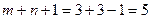 . Умова невиродженості виконана, тому одержуємо опорний розв’язок, який запишемо у вигляді матриці
. Умова невиродженості виконана, тому одержуємо опорний розв’язок, який запишемо у вигляді матриці


| 
| 
| 
| |

| ||||

| ||||

|
 .
.
Вартість перевезень при вихідному опорному розв’язку складає  (грн.).
(грн.).
Перевіримо одержаний розв’язок на оптимальність, для цього знайдемо потенціали зайнятих клітин.

Для вільних клітин знайдемо посередні вартості

Занесемо результати обчислень до таблиці. Знайдемо різниці між тарифами та посередніми вартостями
 Оскільки серед
Оскільки серед  є від’ємне значення, то знайдений розв’язок не є оптимальним і його необхідно покращити. Перейдемо до нового базису за допомогою циклу перерахунку. Для цього представимо функцію у вигляді
є від’ємне значення, то знайдений розв’язок не є оптимальним і його необхідно покращити. Перейдемо до нового базису за допомогою циклу перерахунку. Для цього представимо функцію у вигляді

Маємо один від’ємний коефіцієнт  , тому при його збільшенні функція
, тому при його збільшенні функція 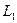 буде зменшуватися. Покладемо
буде зменшуватися. Покладемо  Пересуваємо вантаж
Пересуваємо вантаж  по таблиці
по таблиці  .
.
Одержуємо новий план, який представлений у таблиці.
 .
.
Перевіримо новий план на оптимальність. Для цього повторимо повний цикл розрахунків.
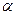
| 
| ||

| 
| 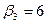
| |

|   2
90 -Р 2
90 -Р
| 5 |  2
7 +Р 2
7 +Р
|

| 4 | ||

|  3
50 +Р 3
50 +Р
| 6 | 60 -Р |


| 
| 
| 
| |

| ||||

| ||||

|


 Представимо функцію у вигляді
Представимо функцію у вигляді

Перейдемо до нового базису
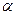
| 
| ||

| 
| 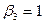
| |

|   2
30 -Р 2
30 -Р
| 5 -2 |  2
60 +Р 2
60 +Р
|

| 4
 5 +Р 5 +Р
| 100 -Р | |

| 6 -1 | 8 3 |


| 
| 
| 
| |

| ||||

| ||||

|



Оскільки серед  немає від’ємних значень, то знайдений розв’язок є оптимальним.
немає від’ємних значень, то знайдений розв’язок є оптимальним.

Задача №4
Для покращення фінансового стану підприємство прийняло рішення про збільшення випуску конкурентноздатної продукції, для чого було вирішено встановити у одному із цехів додаткового обладнання, яке займає  м2 площі. На придбання додаткового обладнання підприємство виділило 10 тис. грн., при цьому воно може придбати обладнання двох видів. Придбання одного комплекту обладнання 1-го виду коштує 1 тис. грн., 2-го виду – 3 тис. грн. Придбання одного комплекту обладнання 1-го виду дозволяє збільшити випуск продукції за зміну на 2 шт., а одного комплекту 2-го виду – на 4 шт. Враховуючи, що для встановлення одного комплекту 1-го виду необхідно 1 м2 площі, а для обладнання 2-го виду – 1 м2 площі. Визначити такий набір додаткового обладнання, який дає можливість максимально збільшити випуск продукції.
м2 площі. На придбання додаткового обладнання підприємство виділило 10 тис. грн., при цьому воно може придбати обладнання двох видів. Придбання одного комплекту обладнання 1-го виду коштує 1 тис. грн., 2-го виду – 3 тис. грн. Придбання одного комплекту обладнання 1-го виду дозволяє збільшити випуск продукції за зміну на 2 шт., а одного комплекту 2-го виду – на 4 шт. Враховуючи, що для встановлення одного комплекту 1-го виду необхідно 1 м2 площі, а для обладнання 2-го виду – 1 м2 площі. Визначити такий набір додаткового обладнання, який дає можливість максимально збільшити випуск продукції.
Припустима, що підприємство придбало  комплектів додаткового обладнання 1-го виду і
комплектів додаткового обладнання 1-го виду і  комплектів обладнання 2-го виду.
комплектів обладнання 2-го виду.
Цільова функція має вигляд

із обмеженнями 
Розв’яжемо задачу методом Гоморі
Спочатку розв’яжемо симплексним методом, для цього перейдемо до канонічної форми системи обмежень
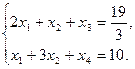

| БЗ | 
| ||||

| 
| 
| 
| |||

| 
| |||||

| 3 | |||||

| -2 | -4 |


| БЗ | 
| ||||

| 
| 
| 
| |||

| 
| 
| ||||

| 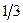
| 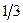
| 
| |||

| 
| 
| 
|
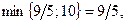

| БЗ | 
| ||||

| 
| 
| 
| |||

| 
| 
| 
| |||

| 
| 
| 
| |||

| 
| 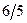
| 
|

Знайдемо дробові частини чисел


Порівняємо

Враховуючи дробові частини чисел  і
і 

 складемо додаткові обмеження цілочислові для першого рядка
складемо додаткові обмеження цілочислові для першого рядка 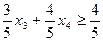 або
або  і введемо додатковий рядок таблиці
і введемо додатковий рядок таблиці

| БЗ | 
| |||||

| 
| 
| 
| 
| |||

| 
| 
| 
| ||||

| 
| 
| 
| ||||

| 
| -1 | 
|

| БЗ | 
| |||||

| 
| 
| 
| 
| |||

| -1 | ||||||

| 
| 
| 
| ||||

| 
| 
| 
| ||||

| 
| 
|

Графічний метод
Областю припустимих розв’язків є чотирьохкутник ОАВС, а  .
.
Оптимальний розв’язок задача має у точці В

 .
.

Одержане оптимальне значення не є цілочисловим. Замінимо багатокутник ОАВС на ОКЕМNF. Лінія рівня переміщується у точку  де і є максимальне значення цільової функції
де і є максимальне значення цільової функції 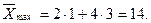
Таким чином, підприємству необхідно придбати 1 комплект обладнання першого виду і 3 комплекти обладнання другого виду, що забезпечить йому при наявних обмеженнях на виробничі площі і грошові кошти максимальне збільшення випуску продукції, яке дорівнює 14 тис. грн. за зміну.
Задача 5
Дослідити функцію на екстремум

- Побудуємо область обмежень
1. 


2. 


3. 



Областю обмежень є множина точок площини ХОУ, що належать чотирьохкутнику АВСDE з вершинами:
А (0;  ); В(
); В( ); С(1,25; 7,5); D(5; 0); E(2; 0)
); С(1,25; 7,5); D(5; 0); E(2; 0)
- Знайдемо значення функції у критичних точках області
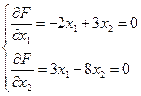

 - критична точка, що не належить області розв’язків.
- критична точка, що не належить області розв’язків.
- Знайдемо значення функції у критичних точках на границях області.
1)  ;
; 


 - критична точка, що належить області розв’язків.
- критична точка, що належить області розв’язків.

2)  ;
;  .
.


 Критична точка
Критична точка  належить області розв’язків, тому
належить області розв’язків, тому 
3) 
 ;
; 
 Критична точка не належить області розв’язків.
Критична точка не належить області розв’язків.
4. Знайдемо значення функції у вершинах області розв’язків
А ( ); В(
); В( ); С(1,25; 7,5); D(5; 0); E(2; 0)
); С(1,25; 7,5); D(5; 0); E(2; 0)