Дано систему т лінійних нерівностей з двома змінними
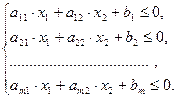 (3.1)
(3.1)
Знак деяких або всіх нерівностей може бути „  ”.
”.
Розглянемо першу нерівність системи (3.1) у системі координат 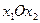 . Побудуємо пряму
. Побудуємо пряму  , яка є граничною прямою. Ця пряма ділить площину на дві півплощини (1) і (2).
, яка є граничною прямою. Ця пряма ділить площину на дві півплощини (1) і (2).

Напівплощина (1) вміщує початок координат. Для визначення, з якого боку від граничної прямої розміщена задана напівплощина необхідно взяти довільну точку на площині (краще початок координат) і підставити координати цієї точки у нерівність. Якщо нерівність справедлива, то напівплощина звернена у бік цієї точки, якщо не справедлива – то у протилежний бік від точки. Напрямок напівплощини на малюнку позначається стрілкою.
Розв’язком кожної нерівності системи є напівплощина, яка вміщує граничну пряму і розміщена по одну сторону від неї.
Перетином напівплощин, кожна з яких визначається відповідною нерівністю системи, називається областю розв’язків системи (ОР).
Область розв’язків системи, яка задовольняє умовам невід’ємності ( ), називається областю невід’ємних або припустимих розв’язків (ОПР).
), називається областю невід’ємних або припустимих розв’язків (ОПР).
Приклад. Знайти ОР і ОПР системи нерівностей і визначити координати кутових точок ОПР.

Знайдемо ОР системи. Для цього побудуємо граничну пряму  і підставимо координати точки
і підставимо координати точки  у нерівність (1):
у нерівність (1):  Координати точки
Координати точки  не задовольняють нерівності (1), тому розв’язком цієї нерівності є напівплощина, що не вміщує точки
не задовольняють нерівності (1), тому розв’язком цієї нерівності є напівплощина, що не вміщує точки  .
.

(1)  При
При  При
При 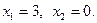
(2)  При
При  При
При 
(3)  При
При  При
При 
(4)  При
При  При
При 
Областю розв’язків і областю припустимих розв’язків є чотирьохкутник  . Знайдемо кутові точки чотирьохкутника.
. Знайдемо кутові точки чотирьохкутника.

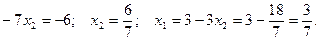
 .
.
 ;
; 
 .
.

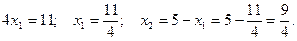
 .
.

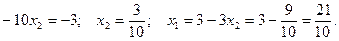
 .
.
Графічний метод
Найбільш простим і наочним методом лінійного програмування є графічний метод. Він застосовується для розв’язання задач лінійного програмування, які задано у неканонічній формі і багатьма змінними у канонічній формі при умові, що вони вміщують не більше двох вільних змінних.
З геометричної точки зору у задачах лінійного програмування відшукується така кутова точка або набір точок із припустимої множини розв’язків, на якій досягається сама верхня (нижня) лінія рівня, розміщена далі (ближче) інших у напрямку найбільш швидкого зростання.
Для знаходження екстремального значення цільової функції при графічному розв’язанні задач лінійного програмування використовують вектор  на площині
на площині 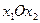 .
.
З курсу вищої математики відомо, що для функції двох змінних  , що є диференційованою у точці
, що є диференційованою у точці  , градієнтом функції
, градієнтом функції  називається вектор, координатами якого є значення частинних похідних у точці
називається вектор, координатами якого є значення частинних похідних у точці  .
.

Градієнт функції характеризує напрямок і величину максимальної швидкості зростання цієї функції у точці.
Для визначення геометричного змісту градієнта функції введемо поняття поверхні рівня.
Поверхнею рівня функції  називається поверхня, на якій ця функція зберігає постійне значення.
називається поверхня, на якій ця функція зберігає постійне значення.

Градієнт функції у даній точці ортогональний до цієї поверхні.
У випадку функції двох змінних, замість поверхні рівня будуть фігурувати лінії рівня.
Надалі будемо позначати градієнт цільової функції  . Цей вектор показує напрямок найшвидшої зміни цільової функції.
. Цей вектор показує напрямок найшвидшої зміни цільової функції.
 ,
,
де  - одиничні вектори за осями
- одиничні вектори за осями  та
та  відповідно.
відповідно.
Таким чином  . Координатами вектора
. Координатами вектора  є коефіцієнти цільової функції
є коефіцієнти цільової функції  .
.
Алгоритм розв’язання задачі
1. Знаходимо область припустимих розв’язків системи обмежень задачі.
2. Будуємо вектор  .
.
3. Проведемо лінію рівня  , яка ортогональна до вектора
, яка ортогональна до вектора  .
.
4. Лінію рівня переміщуємо за напрямком вектора  для задач на максимум і в напрямку протилежному
для задач на максимум і в напрямку протилежному  - для задач на мінімум.
- для задач на мінімум.
Переміщення лінії рівня здійснюється до тих пір, доки у неї не буде тільки однієї спільної точки з областю припустимих розв’язків. Ця точка визначає єдиний розв’язок задачі лінійного програмування і буде точкою екстремуму. Якщо ж лінія рівня буде паралельною одній з сторін області припустимих розв’язків, то у цьому випадку екстремум розглядається у всіх точках відповідної сторони, а задача лінійного програмування буде мати нескінчену множину рішень. У цьому випадку говорять, що така задача має альтернативний оптимум і її розв’язок знаходиться за формулою

де  , а
, а 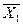 ,
, 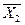 - оптимальні рішення у кутових точках області припустимих розв’язків.
- оптимальні рішення у кутових точках області припустимих розв’язків.
Задача лінійного програмування може бути нерозв’язаною, коли обмеження, що її визначають, будуть суперечними.
5. Знайдемо координати точки екстремуму і значення цільової функції в ній.
Симплексний метод
Симплексний метод є універсальним, оскільки дозволяє розв’язати практично будь-яку задачу лінійного програмування, яка записана у канонічному вигляді.
Ідея симплекс-методу або методу послідовного покращення плану полягає у тому, що починаючи з деякого початкового опорного рішення здійснюється послідовно спрямоване переміщення по опорним рішенням задачі до оптимального. Значення цільової функції при цьому переміщенні для задач на максимум не спадає. Оскільки число опорних рішень є скінченим, то через скінчене число кроків одержують оптимальний опорний розв’язок.
Опорним розв’язком називають базисний невід’ємний розв’язок.
Алгоритм симплексного методу
1. Математична модель задачі повинна бути канонічною.
2. Відшукується вихідний опорний розв’язок і здійснюється перевірка його на оптимальність. Для цього заповнюється симплексна таблиця. Всі рядки таблиці першого кроку за виключенням рядка  (індексний рядок) заповнюються за даними системи обмежень та цільової функції.
(індексний рядок) заповнюються за даними системи обмежень та цільової функції.
БЗ – базисна змінна.
Індексний рядок для змінних визначається за формулою
 ,
, 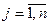 ,
,

| БЗ | 
| 
| ... | 
|  
|

| 
| ... | 
| |||

| 
| 
| 
| ... | 
| 
|

| 
| 
| 
| ... | 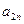
| 
|
| ... | ... | ... | ... | ... | ... | ... |

| 
| 
| 
| ... | 
| 
|

| 
| 
| ... | 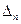
| 
|
для вільного члена за формулою
 .
.
Можливі наступні випадки при розв’язанні задачі на максимум:
- якщо всі оцінки  , то знайдений розв’язок є оптимальним;
, то знайдений розв’язок є оптимальним;
- якщо хоча б одна оцінка  , але при відповідній змінній немає жодного додатного коефіцієнта, розв’язання задачі припиняється, тому що
, але при відповідній змінній немає жодного додатного коефіцієнта, розв’язання задачі припиняється, тому що  , тобто цільова функція є необмеженою у області припустимих розв’язків;
, тобто цільова функція є необмеженою у області припустимих розв’язків;
- якщо хоча б одна оцінка від’ємна, а при відповідній змінній є хоча б один додатній коефіцієнт, то необхідно переходити до другого опорного розв’язку;
- якщо від’ємних оцінок в індексному рядку декілька, то у стовпець базисної змінної (БЗ) вводять ту змінну, якій відповідає найбільша за абсолютною величиною від’ємна оцінка.
Якщо хоча б одна оцінка  , то
, то 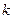 -й стовпець приймається за ключовий. За ключовий рядок приймається такий, якому відповідає мінімальне відношення вільних членів
-й стовпець приймається за ключовий. За ключовий рядок приймається такий, якому відповідає мінімальне відношення вільних членів  до додатних елементів
до додатних елементів 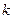 -го стовпця. Елемент, який знаходиться на перетині ключових рядка і стовпця називається ключовим елементом.
-го стовпця. Елемент, який знаходиться на перетині ключових рядка і стовпця називається ключовим елементом.
3. Заповнюється симплексна таблиця другого кроку:
- переписується ключовий рядок, з діленням кожного його елемента на ключовий елемент;
- заповнюється базисний стовпець, при цьому всі елементи окрім ключового дорівнюють нулю;
- решта коефіцієнтів таблиці знаходяться за правилом прямокутника.
Наприклад, якщо  є ключовим елементом, тоді у симплексній таблиці другого кроку
є ключовим елементом, тоді у симплексній таблиці другого кроку
 .
.
Альтернативний оптимум
При розв’язанні задач лінійного програмування симплексним методом за критерій оптимальності приймають умову: оцінка вільних змінних  для задач на максимум і умова
для задач на максимум і умова  для задач на мінімум.
для задач на мінімум.
Якщо на будь-якому кроці хоча б одна з оцінок вільної змінної  , а решта
, а решта  для задач на максимум (
для задач на максимум ( для задач на мінімум), то прийнявши за ключовий стовпець той стовпець, де
для задач на мінімум), то прийнявши за ключовий стовпець той стовпець, де  та знайдемо новий оптимальний розв’язок, при якому значення цільової функції не змінюється. У цьому випадку задача має альтернативний оптимум.
та знайдемо новий оптимальний розв’язок, при якому значення цільової функції не змінюється. У цьому випадку задача має альтернативний оптимум.
Критерієм альтернативного оптимуму при розв’язанні задач симплексним методом є рівність нулю хоча б однієї оцінки вільної змінної  .
.
Якщо тільки одна оцінка вільної змінної дорівнює нулю, тоді розв’язок задачі знаходиться за формулою
 , де
, де  .
.
Якщо дві оцінки і більше, наприклад  , вільних змінних дорівнюють нулю, тоді оптимальний розв’язок знаходиться за формулою
, вільних змінних дорівнюють нулю, тоді оптимальний розв’язок знаходиться за формулою
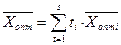 , де
, де 
Транспортна задача
Транспортна задача – одна з розповсюджених задач лінійного програмування. Її мета – розробка найбільш раціональних шляхів і способів транспортування товарів, усунення найбільш віддалених, зустрічних, повторних перевезень. Все це скорочує час просування товарів, зменшує витрати підприємств, пов’язаних із здійсненням процесів забезпечення сировиною, матеріалами, паливом, обладнанням тощо.
У загальному вигляді задачу можна представити наступним чином: у т пунктах виробництва 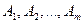 маємо однорідний вантаж відповідно у кількості
маємо однорідний вантаж відповідно у кількості  . Цей вантаж необхідно доставити у п пунктів призначення
. Цей вантаж необхідно доставити у п пунктів призначення  відповідно у кількості
відповідно у кількості  . Вартість перевезення одиниці вантажу (тариф) із пункту
. Вартість перевезення одиниці вантажу (тариф) із пункту  до пункту
до пункту  дорівнює
дорівнює  .
.
Необхідно скласти план перевезень, яких дозволяє перевезти весь вантаж при мінімальних транспортних витратах.
У залежності від співвідношення між сумарними запасами вантажу і сумарними потребами у них, транспортні задачі можуть бути закритими і відкритими.
Якщо  , тоді транспортна задача називається закритою.
, тоді транспортна задача називається закритою.
Якщо  , тоді транспортна задача називається відкритою.
, тоді транспортна задача називається відкритою.
Позначимо через 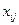 кількість вантажу, який перевозять з пункту
кількість вантажу, який перевозять з пункту  до пункту
до пункту  .
.
Відкрита транспортна задача
Умову даної задачі запишемо у вигляді розподільчої таблиці.
Математична модель закритої транспортної задачі має наступний вид

при обмеженнях




| 
| 
| ... | 
| ... | 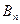
| |

| 
| ... | 
| ... | 
| ||

| 
| 

| 
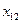
| ... | 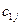

| ... | 

|

| 
| 

| 

| ... | 

| ... | 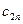
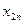
|
| ... | ... | ... | ... | ... | ... | ... | ... |

| 
| 

| 

| ... | 
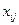
| ... | 

|
| ... | ... | ... | ... | ... | ... | ... | ... |

| 
| 

| 

| ... | 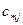

| ... | 

|
Оптимальним розв’язком задачі є матриця  , яка задовольняє системі обмежень і дозволяє мінімізувати цільову функцію.
, яка задовольняє системі обмежень і дозволяє мінімізувати цільову функцію.
Транспортна задача, яка є задачею лінійного програмування, може бути розв’язана симплексним методом, але наявність великої кількості змінних і обмежень робить обчислення громіздкими. Тому для розв’язання транспортних задач розроблено спеціальний метод, який має ті ж самі етапи, що і симплексний метод, а саме:
- знаходження вихідного опорного розв’язку;
- перевірка цього розв’язку на оптимальність;
- перехід від одного опорного розв’язку до іншого.
Знаходження вихідного опорного розв’язку
У розподільчій таблиці клітини, у яких помістимо вантажі, називаються зайнятими і їм відповідають базисні змінні опорного розв’язку. Інші клітини називаються незайнятими або пустими і їм відповідають вільні клітини. У верхньому правому куті кожної клітини будемо записувати тарифи. Існують декілька способів знаходження вихідного опорного розв’язку.
Розглянемо метод мінімального тарифу. Згідно з цим методом, вантажі розподіляються у першу чергу в ті клітини, в яких знаходиться мінімальний тариф перевезень  . У подальшому поставки розподіляються у незайнятих клітинах з найменшими тарифами з урахуванням запасів, що залишилися у постачальників, і задоволення попиту споживачів. Процес розподілу продовжують до тих пір, доки всі вантажі від постачальників не будуть вивезеними, а споживачі не будуть задоволеними. При розподілі вантажів може бути, що кількість зайнятих клітин менше, ніж
. У подальшому поставки розподіляються у незайнятих клітинах з найменшими тарифами з урахуванням запасів, що залишилися у постачальників, і задоволення попиту споживачів. Процес розподілу продовжують до тих пір, доки всі вантажі від постачальників не будуть вивезеними, а споживачі не будуть задоволеними. При розподілі вантажів може бути, що кількість зайнятих клітин менше, ніж  . У цьому випадку недостатня їх кількість заповнюється клітинами з нульовими поставками, такі клітини називаються умовно зайнятими.
. У цьому випадку недостатня їх кількість заповнюється клітинами з нульовими поставками, такі клітини називаються умовно зайнятими.
Нульові поставки розміщують у незайняті клітини з урахуванням найменшого тарифу таким чином, щоб у кожному рядку і стовпці було не менше, ніж по одній зайнятій клітині.
Покращення отриманого опорного плану методом потенціалів
Після завершення першого етапу розв’язку задачі знайдені невідомі можна розбити на дві групи – базисні (зайняті) і вільні.
Представимо цільову функцію наступним чином
 ,
,
де  - вільні змінні;
- вільні змінні;  - знайдений опорний план, а значення
- знайдений опорний план, а значення  отримаємо за допомогою методів потенціалів.
отримаємо за допомогою методів потенціалів.
Поставимо у відповідність кожному з пунктів відправлення вантажів  деяку величину
деяку величину  - „потенціал” пункту
- „потенціал” пункту  . Аналогічно кожному пункту призначення
. Аналогічно кожному пункту призначення  величину
величину 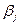 - „потенціалу” пункту
- „потенціалу” пункту  .
.
Для кожного базисного невідомого  складаємо рівняння
складаємо рівняння  , де
, де  - вартість перевезення з пункту
- вартість перевезення з пункту  до пункту
до пункту  . Розв’язуємо систему рівнянь і знаходимо всі потенціали
. Розв’язуємо систему рівнянь і знаходимо всі потенціали  та
та 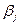 .
.
Тепер для кожної вільної змінної  обчислюємо суму
обчислюємо суму  - посередні вартості та заносимо до таблиці.
- посередні вартості та заносимо до таблиці.
Наступним кроком є визначення різниць 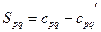 між справжніми вартостями перевезень та посередніми вартостями, які відповідають вільним клітинам.
між справжніми вартостями перевезень та посередніми вартостями, які відповідають вільним клітинам.
Якщо всі величини  невід’ємні, то початковий знайдений розв’язок є оптимальним. Якщо
невід’ємні, то початковий знайдений розв’язок є оптимальним. Якщо  , тоді необхідно перейти до іншого базису.
, тоді необхідно перейти до іншого базису.
Альтернативний оптимум у транспортних задачах
Ознакою наявності альтернативного оптимуму у транспортних задачах є рівність нулю хоча б однієї з оцінок вільних змінних у оптимальному розв’язку  . Зробивши перерозподіл вантажів відносно клітини, що має
. Зробивши перерозподіл вантажів відносно клітини, що має  , одержимо новий оптимальний розв’язок
, одержимо новий оптимальний розв’язок  , при цьому значення цільової функції (транспортних витрат) не зміниться.
, при цьому значення цільової функції (транспортних витрат) не зміниться.
Якщо одна різниця дорівнює нулю, тоді оптимальний розв’язок знаходиться за формулою
 , де
, де  .
.
Виродженість у транспортних задачах
При розв’язанні транспортної задачі може бути, що кількість зайнятих клітин менша за  . У цьому випадку транспортна задача може мати вироджений розв’язок. Для можливого його виключення, доцільно поміняти місцями постачальників і споживачів або ввести у вільну клітину з найменшим тарифом нульову поставку. Нуль вміщують у таку клітину, щоб у кожному рядку і кожному стовпці було не менше однієї зайнятої клітини.
. У цьому випадку транспортна задача може мати вироджений розв’язок. Для можливого його виключення, доцільно поміняти місцями постачальників і споживачів або ввести у вільну клітину з найменшим тарифом нульову поставку. Нуль вміщують у таку клітину, щоб у кожному рядку і кожному стовпці було не менше однієї зайнятої клітини.
Відкрита транспортна задача
При відкритій транспортній задачі сума запасів не співпадає з сумою потреб, тобто  .
.
При цьому:
а). Якщо  , тоді обсяг запасів перевищує обсяг споживання, всі споживачі будуть задоволені повністю і частина запасів залишається не вивезеною. Для розв’язання такої задачі вводять фіктивного (
, тоді обсяг запасів перевищує обсяг споживання, всі споживачі будуть задоволені повністю і частина запасів залишається не вивезеною. Для розв’язання такої задачі вводять фіктивного (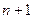 -го) споживача, потреби якого
-го) споживача, потреби якого  .
.
Модель такої задачі набуває вигляду

при обмеженнях


б). Якщо  , тоді обсяги споживання перевищують обсяги запасів і частина споживачів залишається незадоволеною. Для розв’язання такої задачі вводять фіктивного (
, тоді обсяги споживання перевищують обсяги запасів і частина споживачів залишається незадоволеною. Для розв’язання такої задачі вводять фіктивного ( -го) постачальника, обсяги поставок якого
-го) постачальника, обсяги поставок якого  .
.
Модель такої задачі набуває вигляду

при обмеженнях


При введенні фіктивного постачальника або споживача, задача стає закритою і розв’язується за раніше розглянутим алгоритмом, причому тарифи, що відповідають фіктивному постачальнику або споживачу більше або дорівнюють найбільшому з усіх тарифів. У цільовій функції фіктивний постачальник або споживач не враховується.
ЦІЛОЧИСЛОВЕ ПРОГРАМУВАННЯ






