Дробово-лінійне програмування відноситься до методів лінійного програмування, тому що має цільову функцію, записану у нелінійному вигляді. Задача дробово-лінійного програмування у загальному вигляді записується наступним чином

при обмеженнях
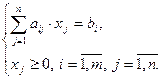 ,
,
де  постійні коефіцієнти і
постійні коефіцієнти і 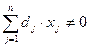 .
.
Графічний метод
Розглянемо задачу дробово-лінійного програмування у вигляді
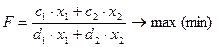 (5.1)
(5.1)
при обмеженнях
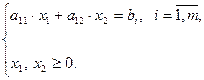 (5.2)
(5.2)
Будемо вважати, що 
Для розв’язання цієї задачі знайдемо область припустимих розв’язків, яка визначається обмеженнями (5.2). Нехай ця область не є пустою множиною.
Із виразу (5.1) знайдемо  :
:

 ,
,
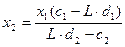 ,
, 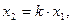 де
де 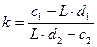 .
.
Пряма 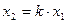 проходить через початок координат. При деякому фіксованому значенні
проходить через початок координат. При деякому фіксованому значенні 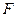 кутовий коефіцієнт
кутовий коефіцієнт 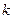 прямої також фіксований і пряма займе певне положення. При зміні значень
прямої також фіксований і пряма займе певне положення. При зміні значень 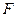 пряма
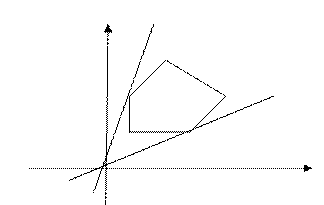
пряма 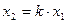 буде повертатися навколо початку координат (див. рисунок).
буде повертатися навколо початку координат (див. рисунок).
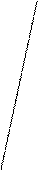

Графічна інтерпретація моделі дробово-лінійного програмування
Встановимо, як буде себе вести кутовий коефіцієнт 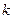 при монотонному зростанні
при монотонному зростанні 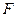 . Знайдемо похідну від
. Знайдемо похідну від 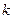 по
по 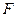 .
.
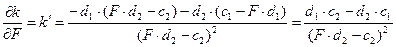 .
.
Знаменник похідної завжди додатній, а чисельник від 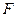 не залежить. Значить, похідна має постійний знак і при збільшенні
не залежить. Значить, похідна має постійний знак і при збільшенні 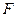 кутовий коефіцієнт буде тільки зростати або тільки спадати, а пряма буде повертатися тільки в одну сторону. Якщо кутовий коефіцієнт прямої має додатнє значення, тоді пряма повертається проти годинникової стрілки, при від’ємному значенні кутового коефіцієнта – за годинниковою стрілкою. Після встановлення напрямку обертання, знаходимо вершину або вершини багатокутника, у яких функція приймає
кутовий коефіцієнт буде тільки зростати або тільки спадати, а пряма буде повертатися тільки в одну сторону. Якщо кутовий коефіцієнт прямої має додатнє значення, тоді пряма повертається проти годинникової стрілки, при від’ємному значенні кутового коефіцієнта – за годинниковою стрілкою. Після встановлення напрямку обертання, знаходимо вершину або вершини багатокутника, у яких функція приймає 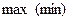 значення, або встановлюємо необмеженість задачі. При цьому можливі наступні випадки.
значення, або встановлюємо необмеженість задачі. При цьому можливі наступні випадки.
1. Область припустимих розв’язків обмежена, максимум і мінімум досягаються у її кутових точках 
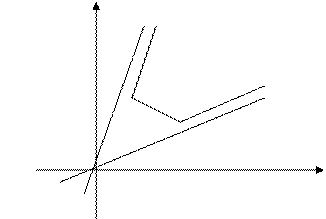
2. Область припустимих розв’язків необмежена, але існують кутові точки, у яких цільова функція приймає максимальне і мінімальне значення

3. Область припустимих розв’язків необмежена і має місце один із екстремумів. Наприклад, мінімум досягається у одній із вершин області і має місце так званий асимптотичний максимум

4. Область припустимих розв’язків необмежена. Максимум і мінімум є асимптотичними
Зведення задачі до симплексного методу
Задачу дробово-лінійного програмування можна звести до задачі лінійного програмування і розв’язати симплексним методом. Для цього позначимо
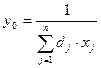 ,
,
при умові
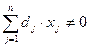
і введемо нові змінні  .
.
Тоді задача набуде вигляду

при обмеженнях
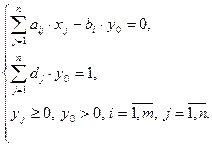
Після знаходження оптимального розв’язку одержаної задачі, і використовуючи вищевикладені співвідношення, знайдемо оптимальний розв’язок вихідної задачі дробово-лінійного програмування.
Метод множників Лагранжа
Нехай задано задачу нелінійного програмування

при обмеженнях
 .
.
Припустимо, що функції  і
і  є неперервними разом із своїми частинними похідними.
є неперервними разом із своїми частинними похідними.
Обмеження задано у вигляді рівностей, тому для розв’язку задачі використаємо метод відшукування умовного екстремуму функції багатьох змінних.
Для розв’язування задачі складається функція Лагранжа

де 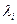 - множники Лагранжа.
- множники Лагранжа.
За необхідною умовою існування екстремуму функції, знайдемо частинні похідні

прирівняємо частинні похідні до нуля і одержимо систему

Розв’язком системи є множина точок, у яких цільова функція 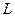 може мати екстремальне значення. Необхідно відмітити, що умови розглянутої системи є необхідними, але не недостатніми. Тому не кожний одержаний розв’язок визначає точку екстремуму цільової функції. Застосування методу буває виправданим, коли заздалегідь припускається існування глобального екстремуму, який співпадає з єдиним локальним максимумом або мінімумом цільової функції.
може мати екстремальне значення. Необхідно відмітити, що умови розглянутої системи є необхідними, але не недостатніми. Тому не кожний одержаний розв’язок визначає точку екстремуму цільової функції. Застосування методу буває виправданим, коли заздалегідь припускається існування глобального екстремуму, який співпадає з єдиним локальним максимумом або мінімумом цільової функції.




