ЛЬВІВСЬКИЙ НАЦІОНАЛЬНИЙ АГРАРНИЙ УНІВЕРСИТЕТ
| Факультет будівництва та архітектури | Кафедра вищої математики |
ОСНОВИ ЧИСЛОВИХ МЕТОДІВ
У ЗАДАЧАХ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ
З РЕАЛІЗАЦІЄЮ В ПАКЕТІ MAPLE
Методичні рекомендації та контрольні завдання до курсу
«Основи числового аналізу» з напряму підготовки 6.100102
«Процеси, машини та обладнання агропромислового виробництва»
Львів 2014
Рекомендовано до друку
методичною радою ЛНАУ
Протокол № 10 від 8.05.2014р.
Укладачі: к. ф.-м.н., доцент Л. Я. Шпак
к. ф.-м.н., доцент Т. І. Бубняк
ст.викладач О. І. Говда
Рецензент: к. т. н., доцент В.О.Тимочко
Видається за редакцією авторів
© Львівський національний аграрний університет, 2014
Основні положення роботи в Maple
Інтерполяційний многочлен
Для функції заданої таблично:
| x | x1 | x2 | … | xn | |
| y | y1 | y2 | … | yn |
інтерполяційний многочлен Лагранжа будуємо згідно формули:
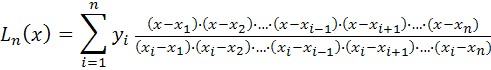
Наприклад, для функції заданої таблично:
| x | -1 | |||||
| y | -3 | -1 | ? |
побудуємо інтерполяційний многочлен Лагранжа.Обчислимо наближене значення многочлена у заданій в точці х = -0,5.
Згідно умови функція визначена в чотирьох точках (вузлах) n =4. Згідно запропонованої формули записуємо чотири доданки:
.
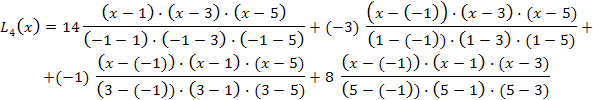Одержуємо многочлен третього порядку:
На рис.1 побудовано графік інтерполяційного многочлена. В вузлах інтерполяції його значення співпадають з значеннями заданими в таблиці.
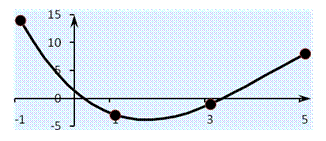
Рис. 1
Обчислюємо значення многочлена в заданій точці:
y = L 4(-0,5)=7,3.
Побудову інтерполяційного многочлена та обчислення його значення в точці (х = -0,5) в вікні програми Maple здійснюємо операторами:
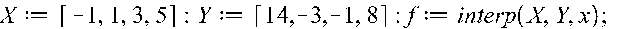
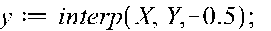
після вводу яких клавішою Enter одержуємо:
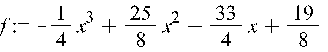
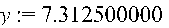
Графік многочлена будуємо оператором:
Треба зауважити, що в діапазоні зміни аргумента х через двокрапку в рядок вказуємо найменше та найбільше його значення з таблиці. Одержуємо графік.
Метод найменших квадратів
3.1 Метод найменших квадратів визначення параметрів
лінійної емпіричної залежності y=ax+b
Нехай в результаті емпіричних досліджень одержано таблицю значень функції:
| x | x1 | x2 | … | xn | |
| y | y1 | y2 | … | yn . |
За методом найменших квадратів для визначення параметрів a та b
лінійної емпіричної залежності y=ax+b мінімізуємо суму квадратів відхилень відповідних значень на прямій і значень заданих в таблиці
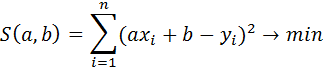
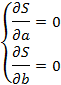З необхідної умови екстремуму функції двох змінних:
записуємо систему двох лінійних рівнянь для визначення параметрів a та b:
Розглянемо приклад. Методом найменших квадратів для функції заданої таблично:
| x | -1 | ||||
| y | -3 | -1 |
визначити параметри a та b емпіричної лінійної залежності y=ax+b.
При обчисленні коефіцієнтів системи та визначенні розв’язку можна скористатись довільним прикладним програмним забезпеченням, зокрема записати в формі Exel таблиці:
| i | x | y | x2 | xy |
| -1 | -14 | |||
| -3 | -3 | |||
| -1 | -3 | |||
| Сума |
Записуємо систему двох лінійних рівнянь: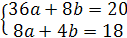 
Розв’язок системи: a =-0,8; b =6,1.
Методом найменших квадратів побудована лінійнаемпірична залежність: y= - 0,8 x+ 6,1.
Побудуємо графік визначеної прямої і точкової функціональної залежності заданої в табличній формі в умові завдання (рис.2).
Рис. 2.
Оскільки параметри прямої визначено методом найменших квадратів то сумарне відхилення точок від прямої є мінімальним.
В вікні програми Maple залежність методом найменших квадратів будуємо підключаючи відповідний статистичний пакет операторами:
> 
> 
> 
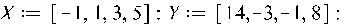
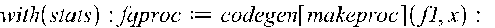
ввівши які одержуємо лінійну залежність
.
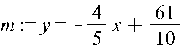3.2 Метод найменших квадратів визначення параметрів
квадратичної емпіричної залежності y=ax2+bx+c
Методом найменших квадратів для функції заданої таблично визначимо параметри a, b та с квадратичноїемпіричної залежності y=ax2+bx+c.
За методом найменших квадратів для визначення параметрів a, b та с
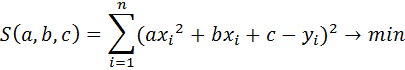для функції заданої таблично аналогічно до попереднього пункту 3.1
мінімізуємо функцію:
і одержуємо систему лінійних рівнянь:
.
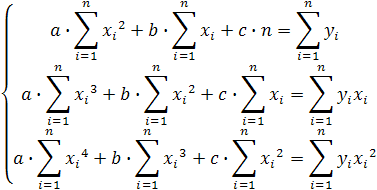Розглянемо числовий приклад залежності для якого в попередньому пункті 3.1 будувалось лінійне наближення і переконаємось, що збільшення степені многочлена у наближенні, а отже збільшення степенів свободи, дозволяє зменшити похибку апроксимації.
Нехай задано таблицю значень функції:
| x | -1 | ||||
| y | -3 | -1 |
При обчислення коефіцієнтів системи та для визначення розв’язку можна скористатись Exel таблицею:
| i | x | y | x2 | x3 | x4 | xy | yx2 |
| -1 | -1 | -14 | |||||
| -3 | -3 | -3 | |||||
| -1 | -3 | -9 | |||||
| Сума | |||||||
Записуємо систему лінійних рівнянь: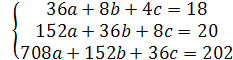 
Розв’язок системи: a =1,625; b =-7,3; c =4,475.
Методом найменших квадратів побудована емпірична залежність: y = 1,625 x 2 - 7,3 x + 4,475.
Побудуємо графік визначеної параболи і точкової функціональної залежності заданої в табличній формі в умові завдання (рис.3). Оскільки параметри визначено методом найменших квадратів то сумарне відхилення точок від параболи є мінімальним.
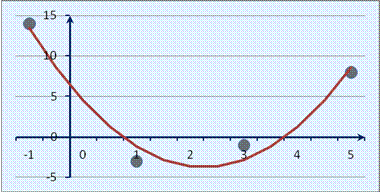
Рис. 3.
В Maple залежності методом найменших квадратів вищих степенів будуємо операторами вже описаними в пункті 3.1:
> 
> 
> 
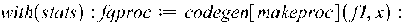
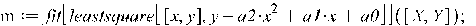
3.3 Метод найменших квадратів визначення параметрів
степеневої емпіричної залежності y=kxm
Числові методи побудови розв’язку задачі Коші
