Теорема Збіжна послідовність має єдину границю.
Доведення. Припустимо, що збіжна послідовність  має дві різні границі
має дві різні границі 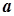 і
і 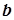 , тобто
, тобто 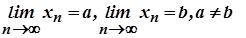 . Тоді
. Тоді 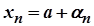 та
та 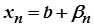 , де
, де 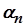 і
і 
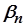 - елементи нескінченно малих послідовностей
- елементи нескінченно малих послідовностей 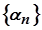 та
та  . Отже,
. Отже, 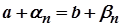 або
або 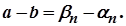 Оскільки
Оскільки  , за властивістю нескінченно малих послідовностей, є елементами нескінченно малої послідовності, а
, за властивістю нескінченно малих послідовностей, є елементами нескінченно малої послідовності, а  постійне число, то
постійне число, то 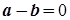 . Таким чином,
. Таким чином, 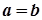 .
.
Теорема. Якщо послідовність  збіжна, то вона обмежена.
збіжна, то вона обмежена.
Доведення. Нехай  і
і 
 - номер, починаючи з якого виконується нерівність
- номер, починаючи з якого виконується нерівність 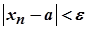 , де
, де 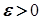 . Тоді
. Тоді
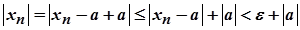
для всіх 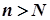 . Виберемо
. Виберемо 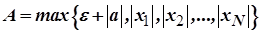 . За цієї умови
. За цієї умови 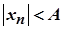 для будь-якого
для будь-якого 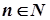 .
.
Зазначимо, що не всяка обмежена послідовність є збіжною. Наприклад, послідовність  обмежена, але не збіжна.
обмежена, але не збіжна.
Теорема 2.6. Якщо  і
і  - збіжні послідовності, то:
- збіжні послідовності, то:
1. Послідовність 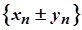 , яка є сумою (різницею) збіжних послідовностей
, яка є сумою (різницею) збіжних послідовностей  та
та  , збіжна і її границя дорівнює сумі (різниці) границь цих послідовностей, тобто
, збіжна і її границя дорівнює сумі (різниці) границь цих послідовностей, тобто 
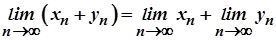 .
.
2. Послідовність  , яка є добутком збіжних послідовностей
, яка є добутком збіжних послідовностей  й
й  , збіжна і її границя дорівнює добутку границь цих послідовностей, тобто
, збіжна і її границя дорівнює добутку границь цих послідовностей, тобто 
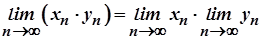 .
.
3. Послідовність 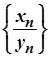 , яка є часткою збіжних послідовностей
, яка є часткою збіжних послідовностей  та
та  , за умови
, за умови 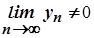 , збіжна і її границя дорівнює частці границь цих послідовностей, тобто
, збіжна і її границя дорівнює частці границь цих послідовностей, тобто 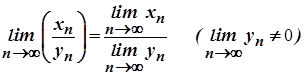 .
.
Доведення. Нехай  і
і  - збіжні послідовності та
- збіжні послідовності та 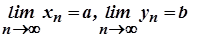 . Тоді
. Тоді 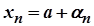 і
і 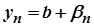 , де
, де 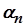 й
й 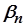 – елементи нескінченно малих послідовностей
– елементи нескінченно малих послідовностей 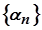 і
і  . Покажемо, що має місце:
. Покажемо, що має місце:
1)  .
.
Оскільки 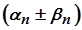 є елементами нескінченно малої послідовності
є елементами нескінченно малої послідовності 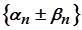 , то звідси випливає, що
, то звідси випливає, що 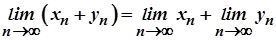 .
.
2) 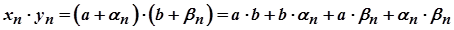 .
.
Оскільки 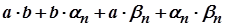 є елементами нескінченно малої послідовності
є елементами нескінченно малої послідовності 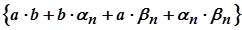 , то
, то 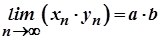 .
.
Тобто 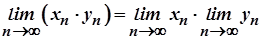 .
.
3) 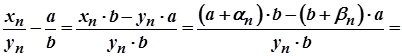
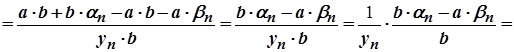
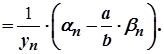
Послідовність  є нескінченно малою. Покажемо, що послідовність
є нескінченно малою. Покажемо, що послідовність 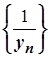 обмежена. Оскільки
обмежена. Оскільки 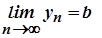 і
і 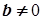 , то для
, то для 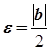 існує такий номер
існує такий номер  , що для всіх
, що для всіх 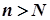 виконується нерівність
виконується нерівність  ,
,
отже, 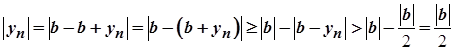 , тобто
, тобто 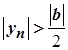 , а тому
, а тому 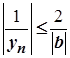 для всіх
для всіх 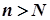 . Звідси випливає, що послідовність
. Звідси випливає, що послідовність 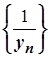 обмежена.
обмежена.
Таким чином, послідовність  нескінченно мала, а тому
нескінченно мала, а тому
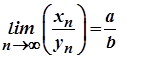 ,
,
тобто
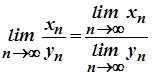 , де
, де 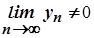 .
.
Зауваження. Пункт 1) наведеної теореми допускає узагальнення на довільне скінченне число доданків. Пункт 2) - на довільне скінченне число множників. Із пункту 2) випливає, що постійний множник можна виносити за знак границі, тобто
 .
.
Невизначені вирази.
Нехай 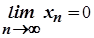 і
і 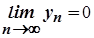 . Виникає питання, що можна сказати про границю
. Виникає питання, що можна сказати про границю 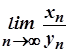 ? Виявляється, що ця границя залежно від окремого закону поведінки змінних
? Виявляється, що ця границя залежно від окремого закону поведінки змінних  та
та 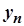 може приймати різні значення або взагалі не існувати.
може приймати різні значення або взагалі не існувати.
Приклади.
1. Якщо  і
і 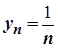 , то
, то  .
.
2. Якщо 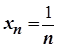 і
і  , то
, то 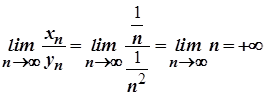 .
.
3. Якщо  і
і 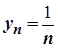 , то
, то 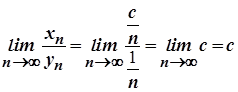 .
.
4. Якщо  і
і 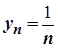 , то
, то  та
та 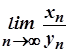 не існує.
не існує.
Отже, лише значення границь числових послідовностей  ,
,  не дозволяє у розглянутому вище випадку робити висновки про значення границі їх відношення. Для того, щоб схарактеризувати цю особливість, говорять, що за умови
не дозволяє у розглянутому вище випадку робити висновки про значення границі їх відношення. Для того, щоб схарактеризувати цю особливість, говорять, що за умови 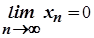 і
і 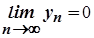 вираз
вираз  є невизначеністю типу
є невизначеністю типу  .
.
Аналогічно невизначеними виразами є:
а) у випадку 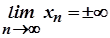 і
і  вираз
вираз  є невизначеністю типу
є невизначеністю типу  ;
;
б) у випадку 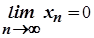 і
і  вираз
вираз 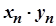 є невизначеністю типу
є невизначеністю типу 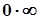 ;
;
в) у випадку  та
та 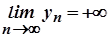 вираз
вираз 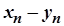 є невизначеністю типу
є невизначеністю типу 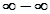 .
.
Для визначення границь невизначених виразів  типу
типу  часто може застосовуватися теорема Штольца, яку ми наведемо без доведення
часто може застосовуватися теорема Штольца, яку ми наведемо без доведення
Теорема. Якщо послідовності 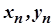 такі, що
такі, що
1) починаючи з деякого номера 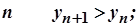
2) 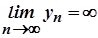 ;
;
3) існує 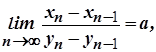
то  .
.
ЛЕКЦІЯ 7
9. Граничний перехід у нерівностях.
10. Монотонні послідовності.
11. Число е.
12. Теорема про вкладені відрізки.






