Розглянемо пряму з фіксованою точкою 
− початком координат. Нехай задана одиниця виміру. Тоді множину дійсних чисел можна поставити у взаємно однозначну відповідність із точками прямої: точці 
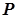, яка лежить справа від точки , поставимо у відповідність число 
, рівне довжині відрізка 
. Тоді 
, яка лежить зліва від точки , число 
, де – довжина відрізка 
, а точці – число 0. Число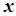 
, яке відповідає точці 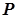, називається координатою точки 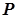. Пряма з описаними властивостями називається числовою прямою. Отже, кожній точці числової прямої відповідає дійсне число – її координата. Має місце й обернене твердження: кожному дійсному числові 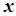відповідає деяка точка числової прямої, а саме точка 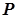, координата якої 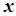. При так установленій відповідності між дійсними числами і точками прямої нерівність 
рівносильна тому, що точка з координатою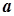 
лежить зліва від точки з координатою 
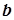. Отже, можна говорити про ізоморфізм множини дійсних чисел і множини точок числової прямої, тобто що числова пряма є моделлю множини дійсних чисел.
Надалі, говорячи про дійсні числа, замість слова "число" іноді вживається слово "точка". У зв'язку з цим числові множини ще називають точковими.
Використовуючи аксіому неперервності множини дійсних чисел, можна встановити, що множина дійсних чисел, яка задовольняє умову 
, є незчисленною. Говорять, що ця множина має потужність континууму. Із цього випливає, що множина всіх дійсних чисел незчисленна. Можна також довести, що множина раціональних чисел зчисленна. Отже, множина ірраціональних чисел незчисленна, оскільки вона є множиною 
(якби множина 
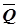ірраціональних чисел була зчисленною, то і множина 
була б зчисленною, оскільки 
).
Найбільш вживані числові множини
Нехай 
. Будемо використовувати наступні позначення:
відрізок,
інтервал,
півінтервал,
півінтервал.
Указані множини ще називають проміжками. Ми розглядатимемо також і нескінченні множини, використовуючи для цього символи 
.
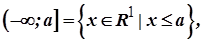
Околом точки 
називається довільний інтервал 
, який містить точку , тобто 
.
Інтервал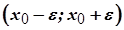 
називається 
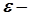околом точки . Точка називається центром цього околу, а число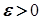 
його радіусом. Зазвичай так позначають околи з центром у точці і дуже малим радіусом, тобто коли 
досить мале.
Межі числових множин
Нехай задано непорожню числову множину 
.
Множина називається обмеженою зверху, якщо існує таке дійсне число 
, що для кожного 
виконується нерівність 
Множина називається обмеженою знизу, якщо існує таке дійсне число 
, що для кожного виконується нерівність 
При цьому числа і називаються відповідно верхньою та нижньою межею множини .
Множина, яка обмежена зверху й знизу, називається обмеженою.
Очевидно, що будь-яка обмежена зверху (знизу) множина має безліч верхніх (нижніх) меж.
Найменша верхня межа обмеженої зверху множини називається точною верхньою межею або верхньою гранню цієї множини і позначається 
(supremum (лат.) – найвище).
Найбільша нижня межа обмеженої знизу множини називається точною нижньою межею або нижньою гранню цієї множини і позначається 
(infimum (лат.) – найнижче).
Якщо 
, то для довільного числа 
існує таке, що 
. Якщо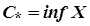 
, то для довільного числа 
існує таке, що 
.
Теорема. Будь-яка непорожня обмежена зверху числова множина має точну верхню межу. Якщо ж вона обмежена знизу, то має точну нижню межу.
Доведення. Нехай – непорожня обмежена зверху числова множина. Тоді множина 
чисел, які обмежують зверху, непорожня. Із означення верхньої межі випливає, що 
виконується нерівність 
. За аксіомою неперервності дійсних чисел існує таке число 
, що виконується нерівність 
.
Із цієї нерівності випливає, що обмежує зверху, тобто є верхньою межею, і є найменшим із усіх верхніх меж, тобто є точною верхньою межею.
Друга частина теореми доводиться аналогічно.
Якщо множина не обмежена зверху (знизу), то за домовленістю пишуть 
.
Абсолютна величина числа
Абсолютноювеличиною (модулем) числа 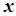називається саме число 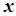, якщо 
, число – 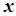, якщо 
.
