Нехай функція  визначена на множині
визначена на множині  і точка
і точка 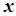 є граничною точкою множини
є граничною точкою множини  . Виберемо із
. Виберемо із  послідовність точок, відмінних від
послідовність точок, відмінних від  :
:  збіжну до
збіжну до  . Значення функції в точках цієї послідовності також утворюють числову послідовність
. Значення функції в точках цієї послідовності також утворюють числову послідовність  .
.
Означення границі функції за Гейне. Число  називається границею функції
називається границею функції  у точці
у точці  (або при
(або при  ), якщо для будь-якої збіжної до
), якщо для будь-якої збіжної до  послідовності значень аргументу
послідовності значень аргументу 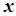 , відмінних від
, відмінних від  , відповідна послідовність значень функції збігається до числа
, відповідна послідовність значень функції збігається до числа  .
.
Символічно це записують так:  .
.
Означення границі функції за Коші. Нехай функція  визначена в деякому околі точки
визначена в деякому околі точки  , крім, можливо, самої точки
, крім, можливо, самої точки  . Число
. Число  називається границею функції
називається границею функції  у точці
у точці  , якщо для довільного числа
, якщо для довільного числа  існує число
існує число  таке, що нерівність
таке, що нерівність  виконується для всіх
виконується для всіх 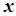 , що задовольняють умову
, що задовольняють умову  .
.
Означення границі функції за Гейне і за Коші еквівалентні.
Дійсно, нехай  згідно з Гейне. Покажемо, що в цьому випадку для довільного числа
згідно з Гейне. Покажемо, що в цьому випадку для довільного числа  існує число
існує число  таке, що нерівність
таке, що нерівність  виконується для всіх
виконується для всіх 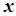 , що задовольняють умову
, що задовольняють умову  , тобто що
, тобто що  згідно з означенням Коші.
згідно з означенням Коші.
Припустимо протилежне. Нехай існує  таке, що для довільного
таке, що для довільного  існує точка
існує точка  , для якої з умови
, для якої з умови  випливає нерівність
випливає нерівність  . Розглянемо послідовність
. Розглянемо послідовність  , де
, де  . Виберемо точки
. Виберемо точки  такі, що
такі, що
 (1)
(1)
і
 . (2)
. (2)
Оскільки  , то
, то  , але за нерівністю (2)
, але за нерівністю (2) 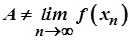 , що суперечить умові, тобто що
, що суперечить умові, тобто що  згідно з Гейне.
згідно з Гейне.
Нехай тепер  згідно з Коші. Покажемо, що
згідно з Коші. Покажемо, що  і згідно з Гейне.
і згідно з Гейне.
Отже, нехай для будь-якого  існує число
існує число  таке, що із нерівності
таке, що із нерівності  випливає нерівність
випливає нерівність  . Виберемо довільну послідовність точок
. Виберемо довільну послідовність точок  збіжну до
збіжну до  . Тоді для значення
. Тоді для значення  , відповідного
, відповідного  , знайдеться такий номер
, знайдеться такий номер  , що для всіх
, що для всіх 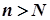 виконуватимуться нерівності
виконуватимуться нерівності  і разом із тим
і разом із тим  . Оскільки вибір
. Оскільки вибір  був довільним, то це означає, що для довільної послідовності
був довільним, то це означає, що для довільної послідовності  із умови
із умови  випливає умова
випливає умова 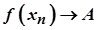 , тобто що
, тобто що  за Гейне.
за Гейне.
Еквівалентність означень границі функції за Гейне і за Коші дає можливість використовувати будь-яке із них залежно від того, яке є більш зручним для розв'язування тієї чи іншої задачі.
Односторонні границі
Число  називається границею функції
називається границею функції  у точці
у точці  справа (зліва), якщо для будь-якої збіжної до
справа (зліва), якщо для будь-якої збіжної до  послідовності
послідовності  , елементи якої більші (менші)
, елементи якої більші (менші)  , відповідна послідовність
, відповідна послідовність  збігається до числа
збігається до числа  .
.
Символічно це записують так:
 .
.
Можна дати рівносильне означення односторонніх границь функції "в термінах  ".
".
Число  називається границею функції
називається границею функції  у точці
у точці  справа (зліва), якщо для довільного числа
справа (зліва), якщо для довільного числа  існує таке
існує таке  , що для всіх
, що для всіх 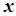 , які задовольняють умову
, які задовольняють умову  , виконується нерівність
, виконується нерівність  .
.
Теорема. Функція  має в точці
має в точці  границю тоді й тільки тоді, коли в цій точці існує як права, так і ліва границя та ці границі рівні між собою. У цьому випадку границя функції дорівнює одностороннім границям.
границю тоді й тільки тоді, коли в цій точці існує як права, так і ліва границя та ці границі рівні між собою. У цьому випадку границя функції дорівнює одностороннім границям.
Доведення. Нехай у точці  існують односторонні границі функції
існують односторонні границі функції  і
і  . Тоді, згідно з означенням односторонніх границь, для будь-якого
. Тоді, згідно з означенням односторонніх границь, для будь-якого  існують числа
існують числа  , такі, що для всіх
, такі, що для всіх 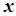 , які задовольняють умову
, які задовольняють умову  , і для всіх
, і для всіх 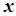 , котрі задовольняють умову
, котрі задовольняють умову  , виконується нерівність
, виконується нерівність  . Виберемо
. Виберемо  . Тоді для всіх
. Тоді для всіх 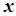 , що задовольняють умову
, що задовольняють умову  , виконуватиметься нерівність
, виконуватиметься нерівність  . Тобто
. Тобто  . З іншого боку, якщо
. З іншого боку, якщо  , то в точці
, то в точці  існують односторонні границі й
існують односторонні границі й  .
.






