Теорема. Сума (різниця) двох нескінченно малих послідовностей є нескінченно малою послідовністю.
Доведення. Нехай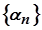 
і 
- нескінченно малі послідовності. Задамо довільне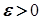 
. Тоді існує такий номер 
, що при 
, й існує такий номер 
, що при 
. Виберемо 
. Тоді при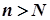 
виконуватимуться нерівност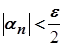і 
і 
. Отже, при
.
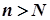
Звідси випливає, що послідовності 
і 
нескінченно малі.
Наслідок. Алгебраїчна сума будь-якого скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю.
Теорема. Добуток обмеженої послідовності на нескінченно малу є нескінченно малою послідовністю.
Доведення. Нехай 
- обмежена послідовність, а 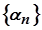- нескінченно мала. Оскільки обмежена, то існує таке число 
, що для всіх 
виконується нерівність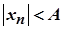 
. Задамо довільне 
. Оскільки послідовність 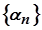нескінченно мала, то існує такий номер 
, що при 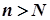виконується нерівність 
. Отже, при
.
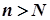
Звідси випливає, що послідовність 
нескінченно мала.
Наслідок 1. Добуток нескінченно малої послідовності на число є нескінченно малою послідовністю.
Наслідок 2. Добуток двох нескінченно малих послідовностей є нескінченно малою послідовністю.
Дійсно, якщо послідовність 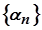нескінченно мала, то вона обмежена. Отже, добуток двох нескінченно малих послідовностей можна розглядати як добуток нескінченно малої послідовності на обмежену.
Із наслідку 2 випливає, що добуток скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю.
Зауваження. Стосовно частки двох нескінченно малих послідовностей у загальному випадку нічого сказати не можна, оскільки вона може бути нескінченно малою, постійною, нескінченно великою послідовністю або взагалі не визначеною.
ЛЕКЦІЯ 6
6. Збіжні послідовності.
7. Властивості збіжних послідовностей.
8. Невизначені вирази.
Збіжні послідовності
Границя числової послідовності. Число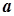 
називається границею послідовності , якщо для будь-якого числа 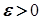існує такий номер , що для всіх членів послідовності із номером 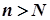виконується нерівність
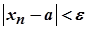. (2)
Якщо число 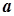є границею послідовності , то пишуть
,
а саму послідовність називають збіжною.
Послідовність, яка не є збіжною, називається розбіжною.
Приклад. Довести, що 
.
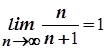Доведення. Задамо довільне число 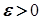і покажемо, що існує таке натуральне число , що для всіх членів послідовності із номером 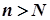виконується нерівність 
.
Оскільки 
, то
.
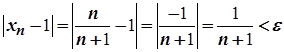Розв'язавши відносно 
нерівність 
, маємо 
.
Якщо в значенні узяти цілу частину числа 
, тобто покласти 
, то нерівність 
<ε виконується для всіх 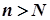. Отже, .
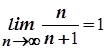Якщо послідовність збіжна і , то будь-який її елемент можна подати у вигляді 
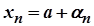, де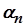 
- елемент нескінченно малої послідовності .
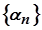Дійсно, якщо , то послідовність 
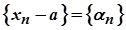є нескінченно малою, оскільки для будь-якого 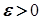існує такий номер 
, що для 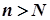виконується нерівність 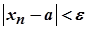, тобто 
.
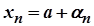Має місце й обернене твердження. Якщо можна подати у вигляді , де 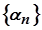- нескінченно мала послідовність, то .
Нерівність (2) рівносильна нерівності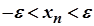 
або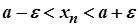 
,
із якої випливає, що знаходиться в 
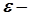околі точки 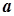. Отже, означення границі числової послідовності можна дати наступним чином.
Число 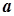називається границею послідовності , якщо для будь-якого числа 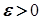існує такий номер , що всі члени послідовності із номером 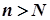знаходяться в 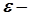околі точки .
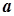Очевидно, що нескінченно велика послідовність не має границі. Іноді говорять, що вона має нескінченну границю і пишуть
.
Якщо при цьому, починаючи з деякого номера, всі члени послідовності додатні (від'ємні), то пишуть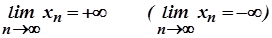 
.
Усяка нескінченно мала послідовність 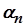збіжна, причому 
.
Це безпосередньо випливає з означення границі числової послідовності й означення нескінченно малої числової послідовності.
