Абсолютна величина числа позначається символом

 

 

Із означення абсолютної величини випливає, що нерівності і , де рівносильні, тобто .

Теорема. Абсолютна величина суми двох чисел не більше від суми абсолютних величин чисел, тобто .

Доведення. За означення абсолютної величини

 

 

для будь-яких чисел 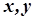. Додаючи почленно ці нерівності, одержимо

 

.

 

Остання нерівність рівносильна нерівності

 

.

 

Теорема. Абсолютна величина різниці двох чисел не менше від різниці абсолютних величин чисел, тобто

 

.

 

Доведення. Для будь-яких чисел 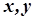маємо

 

 

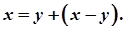
За попередньою теоремою

 

.

 

Звідси одержуємо

.

 

Зазначимо, що мають місце співвідношення

 

 

ТЕМА 2. ЧИСЛОВІ ПОСЛІДОВНОСТІ

 

ЛЕКЦІЯ 5

 

1. Означення числової послідовності.

2. Арифметичні дії над числовими послідовностями.

3. Обмежені і необмежені числові послідовності.

4. Нескінченно малі і нескінченно великі послідовності.

5. Основні властивості нескінченно малих послідовностей.

 

 

Означення числової послідовності

 

 

Числовою послідовністю називається відображення .

Отже, якщо кожному натуральному числові поставлено у відповідність дійсне число , то множина дійсних чисел

 

(1)

 

називається числовою послідовністю.

Числа називаються елементами (або членами) послідовності. Символ називається загальним елементом послідовності, а його номером. Скорочено послідовність (1) позначається так: . Наприклад, є послідовність .

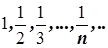Послідовність вважається заданою, якщо вказано правило, за яким кожному натуральному числові поставлено у відповідність дійсне число . Найчастіше числову послідовність задають формулою загального ( го) члена послідовності: . Наприклад, формула задає числову послідовність

 

Числову послідовність можна задати рекурентною формулою, тобто формулою, в якій указується правило, за котрим можна виразити наступний її член через попередні. Наприклад, арифметична прогресія з першим членом та різницею визначається рекурентною формулою

 

або .

 

Рекурентною формулою

 

 

задається послідовність

 

1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…,

 

що відома в математиці як " ряд Фібоначчі", а її члени – як числа Фібоначчі. Ці числа мають ряд цікавих властивостей. Нині вони використовуються при обробці інформації на ЕОМ, при відшуканні оптимальних методів програмування тощо.

 

Арифметичні дії над числовими послідовностями

 

 

Нехай задано послідовності і.

Добутком послідовності на число називається послідовність , тобто

 

.

 

Сумою послідовностей і називається послідовність :

 

;

 

різницею – послідовність :

 

;

 

добутком – послідовність :

 

;

 

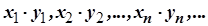часткою - послідовність :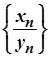

 

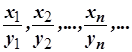; де .